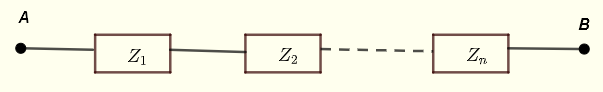
Die äquivalente Impedanz zwischen den Punkten A und B wird durch
\[ Z_{AB} = Z_1 + Z_2 + ... + Z_n \] gegeben.
Hier wird erklärt, wie komplexe Impedanzen verwendet werden, um die äquivalenten Impedanzen von Reihen- und Parallelimpedanzen in Wechselstromkreisen zu berechnen. Alle Schritte werden symbolisch gezeigt und dann werden numerische Werte verwendet.
Da das Symbol \( i \) für Ströme in Wechselstromkreisen verwendet wird, verwenden wir hier \( j \) als imaginäre Einheit, definiert durch \( j^2 = -1 \) oder \( j = \sqrt{-1} \).
Seien \( Z_1 \), \( Z_2 \) ... \( Z_n \) Impedanzen in Reihe wie unten dargestellt.
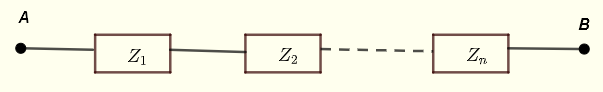
Die äquivalente Impedanz zwischen den Punkten A und B wird durch
\[ Z_{AB} = Z_1 + Z_2 + ... + Z_n \]
gegeben.
Beispiel 1
Finde die komplexe Impedanz, die dem gezeigten Reihen-RLC-Kreis entspricht, gegeben:
Frequenz \( f = 1 \; kHz \), \( C = 10 \; \mu F \), \( L = 10 \; mH \) und \( R = 100 \; \Omega \)

Lösung zu Beispiel 1
Sei
\( Z_R = R \), \( Z_C = \dfrac{1}{j \omega C} = \dfrac{-j}{\omega C} \), \( Z_L = j \omega L\)
Wende die Regel der Impedanzen eines Reihenstromkreises an
\( Z_{AB} = Z_R + Z_C + Z_L = R - \dfrac{j}{\omega C} + j \omega L \)
Sei
\( X_L = \omega L = 2 \pi f L \) und \( X_C = \dfrac{1}{\omega C} = \dfrac{1}{2 \pi f C} \)
und schreibe \( Z_{AB} \) um:
\( Z_{AB} = R + j(X_L - X_C) \)
Substituiere mit numerischen Werten:
\( X_L = \omega L = 2 \pi f L = 2 \pi 10^3 \times 10^{-2} = 62.83 \Omega \)
\( X_C = \dfrac{1}{\omega C} = \dfrac{1}{2 \pi f C} = \dfrac{1}{2 \pi 10^3 \times 10^{-5}} = 15.92 \Omega \)
Gruppiere die imaginären Terme:
\( Z_{AB} = 100 + j ( 62.83 - 15.92 ) \)
Vereinfache:
\( Z_{AB} = 100 + j ( 62.83 - 15.92 ) = 100 + 46.91 j\)
Schreibe das Obige in Exponentialform:
\( Z_{AB} = \sqrt {100^2 + 46.91^2} e^{j \arctan{\dfrac{46.91}{100}}} = 110.45 e^{j 0.44} \)
\( Z_{AB} \) in Phasenform geschrieben:
\( Z_{AB} = 110.45 \angle 0.44 \; rad = 110.45 \angle 25.13^{\circ} \)
Ein Reihen-RLC-Schaltungsimpedanz-Rechner kann für weitere Übungen verwendet werden.
Seien \( Z_1 \), \( Z_2 \) ... \( Z_n \) Impedanzen in Parallel wie unten dargestellt.
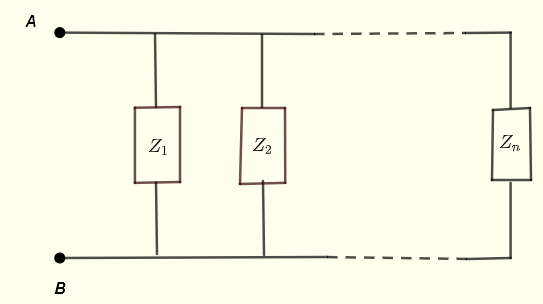
Die äquivalente Impedanz zwischen den Punkten A und B wird durch
\[ \dfrac{1}{Z_{AB}} = \dfrac{1}{Z_1} + \dfrac{1}{Z_2} + ... + \dfrac{1}{Z_n} \]
gegeben.
Beispiel 2
Finde die komplexe Impedanz, die dem gezeigten parallelen RLC-Kreis entspricht, gegeben:
Frequenz \( f = 1,5 \; kHz \), \( C = 15 \; \mu F \), \( L = 20 \; mH \) und \( R = 50 \; \Omega \)

Lösung zu Beispiel 2
Sei
\( Z_R = R \), \( Z_C = \dfrac{1}{j \omega C} \), \( Z_L = j \omega L\)
Wende die Regel der Impedanzen eines Parallelstromkreises an:
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{Z_R} + \dfrac{1}{Z_C} + \dfrac{1}{Z_L} \)
\( = \dfrac{1}{R} + \dfrac{1}{\dfrac{1}{j \omega C}} + \dfrac{1}{j \omega L} \)
Sei
\( X_L = \omega L \) und \( X_C = \dfrac{1}{\omega C} \)
und schreibe das Obige um:
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{R} + \dfrac{1}{\dfrac{X_C}{j}} + \dfrac{1}{j X_L} \)
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{R} + j (\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} ) \)
Der Betrag \( r \) der obigen komplexen Zahl wird durch
\( r = \sqrt { (\dfrac{1}{R})^2 + (\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} )^2} \)
und sein Argument \( \alpha \) durch
\( \alpha = \arctan \left(\dfrac{\dfrac{1}{{X_C}} - \dfrac{1}{ X_L}}{\dfrac{1}{R}} \right) \)
\( = \arctan \left(\dfrac{R}{X_C}-\dfrac{R}{X_L} \right) \)
Wir verwenden jetzt die Exponentialform der komplexen Zahl, um zu schreiben:
\( \dfrac{1}{Z_{AB}} = r e^{j\alpha} \)
Wir schreiben die äquivalente Impedanz \( Z_{AB} \) als komplexe Zahl in Exponentialform:
\( Z_{AB} = \dfrac{1}{r} e^{-j \alpha} \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} e^{-j \arctan \left(\dfrac{R}{X_C}-\dfrac{R}{X_L} \right) } \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} e^{j \arctan \left(\dfrac{R}{X_L}-\dfrac{R}{X_C} \right) } \)
Wir verwenden jetzt die angegebenen Werte:
\( f = 1,5 \; kHz \), \( C = 15 \; \mu F \), \( L = 20 \; mH \) und \( R = 50 \; \Omega \)
\( X_L = \omega L = 2 \pi f L = 2 \pi 1,5 \times 10^3 \times 20 10^{-3} = 188,50 \)
\( X_C = \dfrac{1}{\omega C} = \dfrac{1}{ 2\pi f C} = \dfrac{1}{ 2\pi 1,5 \times 10^3 \times 15 10^{-6}} = 7,07\)
Betrag: \( \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{50}\right)^2 + \left(\dfrac{1}{{7,07}} - \dfrac{1}{ 188,50} \right)^2}} \)
\( = 7,27 \)
Argument: \( \arctan \left(\dfrac{R}{X_L}-\dfrac{R}{X_C} \right) \)
\( = \arctan \left(\dfrac{50}{188,50}-\dfrac{50}{7,07} \right) \)
\( = -81,64^{\circ} \)
Ein Parallel-RLC-Schaltungsimpedanz-Rechner kann für weitere Übungen verwendet werden.