Verwendung komplexer Zahlen in Wechselstromkreisen

Inhaltsverzeichnis

Hier wird erläutert, wie komplexe Zahlen zur Analyse und Berechnung von Strömen und Spannungen in Wechselstromkreisen (AC) verwendet werden können und wie der Widerstand, die Impedanz eines Kondensators und die Impedanz einer Induktivität durch komplexe Zahlen dargestellt werden. Es wird auch gezeigt, wie die Verwendung von komplexen Impedanzen die Anwendung eines Gesetzes ähnlich dem Ohmschen Gesetz ermöglicht, um Wechselstromkreise mathematisch zu modellieren.
Zwei Hauptgründe, warum sich die Verwendung komplexer Zahlen zur Modellierung von Wechselstromkreisen und vieler anderer Sinuswellenphänomene in verschiedenen Ingenieurbereichen eignet, sind:
1) Die Wechselstromsignale (und viele andere Sinuswellenphänomene) sind durch eine Amplitude und eine Phase gekennzeichnet, die in etwa dem Modul und dem Argument komplexer Zahlen entsprechen.
2) Grundlegende Operationen wie Addition, Subtraktion, Multiplikation und Division komplexer Zahlen sind einfacher durchzuführen und auf einem Computer zu programmieren.
Hinweis
1) Da das Symbol \( i \) für Ströme in Wechselstromkreisen verwendet wird, verwenden wir hier \( j \) als imaginäre Einheit, definiert durch \( j^2 = -1 \) oder \( j = \sqrt{-1} \).
2) Das Symbol \( \Re e\) repräsentiert den Realteil einer komplexen Zahl.

A - Realteil komplexer Zahlen

Eine komplexe Zahl in Standardform \( Z = a + j b \) kann in exponentieller Form wie folgt geschrieben werden:
\( \displaystyle Z = r e^{j \theta} \)      mit \( j^2 = -1 \)
und in Polarform wie folgt
\( Z = r \angle \theta \)
wobei \( r = \sqrt{a^2 +b^2} \) das Modul von \( Z \) ist und \( \tan \theta = \dfrac{b}{a} \) sein Argument.
Nehmen Sie den Realteil, geschrieben als \( \Re e \), von jeder Seite einer komplexen Zahl in exponentieller Form
\( \Re e (r e^{j \theta}) = \Re e (r ( \cos \theta + j \sin \theta )) = \Re e (r \cos \theta + j r \sin \theta ) = r \cos \theta \)
Im Folgenden bedeutet \( \Re e \) den Realteil einer gegebenen komplexen Zahl.

B - Ableitung komplexer Funktionen mit einer Variablen

Sei \( f(t) \) eine komplexe Funktion mit einer Variablen \( t \), die in der Form geschrieben ist:
\( f(t) = a(t) + j b(t) \)
wobei \( a(t) \) der Realteil von \( f(t) \) ist, \( b(t) \) der Imaginärteil von \( f(t) \) und \( j = \sqrt {-1}\) die imaginäre Einheit ist.
Sei \( f'(t) \) die erste Ableitung von \( f(t) \) bezüglich \( t \), definiert durch:
\( f'(t) = \lim_{h\to 0} \dfrac{f(t+h) - f(t) }{h} \)
Ersetzen Sie \( f(t+h) \) durch \( a(t+h) + j b(t+h) \) in der obigen Formel.
\( f'(t) = \lim_{h\to 0} \dfrac{ a(t+h) + j b(t+h) - (a(t) + jb(t))}{h} \)
Trennen Sie die Terme wie folgt auf:
\( f'(t) = \lim_{h\to 0} \dfrac{ a(t+h) - a(t)}{h} + j \lim_{h\to 0} \dfrac{ j b(t+h) - jb(t))}{h} \)
\( f'(t) = a'(t) + j b'(t) \)
Es ist nun leicht zu zeigen, dass der Realteil der Ableitung von \( f(t) \) gleich der Ableitung des Realteils von \( f(t) \) ist, was geschrieben werden kann als:
\( \Re e(f'(t)) = a'(t) = (\Re e(f(t))' \)
oder
\( \Re e \left ( \dfrac{df(t)}{dt} \right) = \dfrac {d a(t)}{dt} = \dfrac {d \left (\Re e(f(t)) \right)}{dt} \)

C - Integral komplexer Funktionen mit einer Variablen

Sei \( f(t) \) eine komplexe Funktion mit einer Variablen \( t \), die in der Form geschrieben ist:
\( f(t) = a(t) + j b(t) \)
wobei \( a(t) \) der Realteil von \( f(t) \) ist, \( b(t) \) der Imaginärteil von \( f(t) \) und \( j = \sqrt {-1}\) die imaginäre Einheit ist.
Sei \( F(t) \) definiert durch das unbestimmte Integral:
\( \displaystyle F(t) = \int f(t) dt = \int (a(t) + j b(t)) dt = \int a(t) dt + j \int b(t) dt \)
Es ist nun leicht zu zeigen, dass der Realteil des unbestimmten Integrals von \( f(t) \) gleich dem unbestimmten Integral des Realteils von \( f(t) \) ist, was geschrieben werden kann als:
\( \displaystyle \Re e \left( \int f(t) dt \right) = \int a(t) dt = \int \left( \Re e f(t) \right) dt \)

Wir verwenden nun die obigen Konzepte, um einfache Wechselstromkreise unter Verwendung komplexer Zahlen zu analysieren.

D - Wechselspannungsquelle und komplexe Zahlen

Im Folgenden ist \( v(t) \) eine Wechselspannungsquelle, die mit der Zeit \( t \) variiert und gegeben ist durch:
\( v(t) = V_0 \cos(\omega t) \)
wobei \( V_0 \) eine reelle Zahl ist, die der Spitzenspannung entspricht, und \( \omega = 2 \pi f \) ebenfalls eine reelle Zahl ist, wobei \( f \) die Frequenz der Spannungsquelle ist.
Unter Verwendung komplexer Zahlen kann \( v(t) \) auch geschrieben werden als:
\( v(t) = V_0 \cos(\omega t) = \Re e ( V_0 \cos(\omega t) + j V_0 \sin(\omega t) ) = \Re e (V_0 e^{j\omega t} ) \)

E - Widerstand im Wechselstromkreis

Betrachten wir einen einfachen Wechselstromkreis mit einem Widerstand, wie unten gezeigt. Sei \( v(t) \) eine Wechselspannungsquelle, gegeben durch:
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
wobei \( V_0 \) und \( \omega \) reelle Größen sind.


Die Beziehung zwischen dem Strom \( i \) durch und der Spannung \( v(t)_R \) über den Widerstand \( R \) wird gegeben durch:
\( v(t)_R = R i \)
Unter Verwendung der oben gezeigten Einzelschleife haben wir:
\( v(t) = v(t)_R \)
\( v(t) \) ist gegeben durch \( v(t) = V_0 \cos(\omega t) \)
daher:
\( v(t)_R = V_0 cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
Durch die Kombination der obigen Gleichungen schreiben wir:
\( R i = \Re e (V_0 e^{j\omega t} ) \)       (I)
Sei \( V_R = V_0 e^{j\omega t} \) und schreiben Sie (I) oben um als:
\( R i = \Re e V_R \)
Da \( R \) eine reelle Größe ist, kann das oben genannte geschrieben werden als:
\( i = \Re e \left( \dfrac{V_R }{R} \right) \)
Sei \( Z_R \) definiert als die Impedanz eines Widerstands, so dass:
\( Z_R = R \)
Da \( R \) reell ist, ist die Impedanz \( Z_R \) eines Widerstands eine reelle Zahl.
Der Strom \( i \) kann dann geschrieben werden als:
\( i = \Re e \left( \dfrac{ V_R } {Z_R} \right) \)
Sei:
\( I = \dfrac{ V_R } {Z_R} \)
Das oben Gesagte ergibt eine Beziehung, die dem Ohmschen Gesetz in Gleichstromkreisen (DC) ähnelt. Die obige Beziehung zwischen komplexen Größen \( I \), \( V_R \) und \( R \) erleichtert die Berechnungen erheblich.
Dies vereinfacht die Berechnungen insofern, als wir Berechnungen mit komplexen Impedanzen, Spannungen und Strömen durchführen und dann den Realteil als endgültige Antwort nehmen.

F - Kondensator im Wechselstromkreis

Betrachten wir einen einfachen Wechselstromkreis mit einem Kondensator, wie unten gezeigt. Sei \( v(t) \) eine Wechselspannungsquelle, gegeben durch:
\( v(t) = V_0 cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)

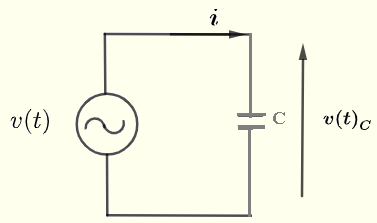
Die Beziehung zwischen dem Strom \( i \) durch und der Spannung \( v(t)_C \) über den Kondensator \( C \) wird gegeben durch:
\( \displaystyle v(t)_C = \dfrac{1}{C} \int i dt \)
Unter Verwendung der oben gezeigten Einzelschleife haben wir:
\( v(t) = v(t)_C \)
Gegeben:
\( v(t) = V_0 cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
kombinieren wir all das oben Genannte und schreiben:
\( \displaystyle \Re e (V_0 e^{j\omega t} ) = \dfrac{1}{C} \int i dt \)
Nehmen Sie die Ableitung beider Seiten:
\( \displaystyle \dfrac{d}{dt} (\Re e (V_0 e^{j\omega t}) ) = \dfrac{d}{dt} \left(\dfrac{1}{C} \int i dt \right) \)
Verwenden Sie das oben in Teil B besprochene Ergebnis, und schreiben Sie das oben Genannte um als:
\( \displaystyle \Re e \dfrac{d}{dt} \left( V_0 e^{j\omega t} \right) = \dfrac{d}{dt} \left(\dfrac{1}{C} \int i dt \right) \)
Vereinfachen Sie:
\( \Re e \left( j \omega V_0 e^{j\omega t} \right) = \dfrac{1}{C} i \)
Da die Kapazität \( C \) eine reelle Größe ist, können wir schreiben:
\( i = \Re e \left( j \omega C \; V_0 e^{j\omega t} \right) \)
Sei \( V_C = V_0 e^{j\omega t} \) und definieren Sie \( Z_C \) als die komplexe Impedanz eines Kondensators, so dass:
\( Z_C = \dfrac{1}{j \omega C} = - \dfrac {j} { \omega C} \)
Da \( C \) reell ist, ist die Impedanz \( Z_C \) eines Kondensators eine rein imaginäre Zahl.
Der Strom \( i \) kann dann geschrieben werden als:
\( i = \Re e \left( \dfrac{ V_C } {Z_C} \right) \)
Sei:
\( I = \dfrac{ V_C } {Z_C} \)
Das oben Gesagte ähnelt dem Ohmschen Gesetz in Gleichstromkreisen (DC). Die obige Beziehung zwischen komplexen Größen \( I \), \( V_C \) und \( Z_C \) erleichtert die Berechnungen erheblich.
Dies vereinfacht die Berechnungen insofern, als wir Berechnungen mit komplexen Impedanzen, Spannungen und Strömen durchführen und dann den Realteil als endgültige Antwort nehmen.

G - Induktivität im Wechselstromkreis

Betrachten wir einen einfachen Wechselstromkreis mit einer Induktivität, wie unten gezeigt. Sei \( v(t) \) eine Wechselspannungsquelle, gegeben durch:
\( v(t) = V_0 cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)

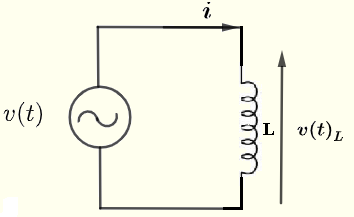
Die Beziehung zwischen dem Strom \( i \) durch und der Spannung \( v(t)_L \) über die Induktivität mit Induktivität \( L \) wird gegeben durch:
\( v(t)_L = L \dfrac {d i}{ dt} \)
Unter Verwendung der oben gezeigten Einzelschleife haben wir:
\( v(t) = v(t)_L \)
Gegeben:
\( v(t) = V_0 cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
kombinieren wir all das oben Genannte und schreiben:
\( \Re e (V_0 e^{j\omega t} ) = L \dfrac {d i}{ dt} \)
Nehmen Sie das unbestimmte Integral beider Seiten:
\( \displaystyle \int \Re e (V_0 e^{j\omega t}) dt = \int L \dfrac {d i}{ dt} dt \)
Verwenden Sie das bereits in Teil C besprochene Ergebnis, und schreiben Sie das oben Genannte um als:
\( \displaystyle \Re e \int V_0 e^{j\omega t} dt = \int L \dfrac {d i}{ dt} dt \)
Berechnen Sie die Integrale auf beiden Seiten:
\( \Re e \left( \dfrac{1}{j\omega} V_0 e^{j\omega t} \right) = L i \)
Da die Induktivität \( L \) eine reelle Größe ist, können wir schreiben:
\( i = \Re e \left( \dfrac{1}{j \omega L} \; V_0 e^{j\omega t} \right) \)
Sei \( V_L = V_0 e^{j\omega t} \) und \( Z_L \) definiert als die Impedanz einer Induktivität, so dass:
\( Z_L = j \omega L \)
Da \( L \) reell ist, ist die Impedanz \( Z_L \) einer Induktivität eine rein imaginäre Zahl.
Der Strom \( i \) kann dann geschrieben werden als:
\( i = \Re e \left( \dfrac{ V_L } {Z_L} \right) \)
Sei:
\( I = \dfrac{ V_L } {Z_L} \)
Das oben Gesagte ergibt eine Beziehung, die dem Ohmschen Gesetz zwischen komplexen Größen \( I \), \( V_L \) und \( Z_L \) ähnelt.
Dies vereinfacht die Berechnungen insofern, als wir Berechnungen mit komplexen Impedanzen, Spannungen und Strömen durchführen und dann den Realteil als endgültige Antwort nehmen.

H - Fazit: Ohmsches Gesetz mit komplexen Impedanzen

Wir haben oben gesehen, dass die Impedanzen von Widerständen, Kondensatoren und Induktivitäten als komplexe Größen definiert werden können, die entweder rein reell oder rein imaginär sind und durch folgende Gleichungen gegeben sind:
1) Für einen Widerstand \( R\) ; die Impedanz wird gegeben durch: \[ Z_R = R \] und die Beziehung zwischen dem Strom \( I \) (in komplexer Form) durch und der Spannung \( V_R \) (in komplexer Form) über den Widerstand \( R \) ist das Ohmsche Gesetz im Wechselstrom und wird gegeben durch: \[ I = \dfrac{V_R}{Z_R} \] 2) Für einen Kondensator \( C \) ; die Impedanz wird gegeben durch: \[ Z_C = -\dfrac{j}{\omega C} \] und die Beziehung zwischen dem Strom \( I \) (in komplexer Form) durch und der Spannung \( V_C \) (in komplexer Form) über den Kondensator \( C \) ist das Ohmsche Gesetz im Wechselstrom und wird gegeben durch: \[ I = \dfrac{V_C}{Z_C} \] 3) Für eine Induktivität \( L \) ; die Impedanz wird gegeben durch: \[ Z_L = j \omega L \] und die Beziehung zwischen dem Strom \( I \) (in komplexer Form) durch und der Spannung \( V_L \) (in komplexer Form) über die Induktivität \( L \) ist das Ohmsche Gesetz im Wechselstrom und wird gegeben durch: \[ I = \dfrac{V_C}{Z_L} \] Wir kommen zu dem Schluss, dass das Ohmsche Gesetz auch im Wechselstromkreis gilt, wenn komplexe Zahlen verwendet werden, um die Impedanzen von Widerständen, Kondensatoren und Induktivitäten zu modellieren.
Es kann auch gezeigt werden, dass die Kirchhoffschen Gesetze auch im Wechselstromkreis gelten, wenn komplexe Zahlen verwendet werden, um die Impedanzen von Widerständen, Kondensatoren und Induktivitäten zu modellieren.
Äquivalente Impedanzen für Reihen- und Parallelimpedanzen können mit ähnlichen Regeln wie für Reihen- und Parallelwiderstände berechnet werden.

I - Beispiele mit Lösungen

Beispiel 1
Bestimmen Sie den Strom \( i \), die Spannung \( v(t)_R \) über den Widerstand \( R \) und die Spannung \( v(t)_L \) über die Induktivität \( L \) in Abhängigkeit von \( V_0 \), \( R \), \( L \) und \( \omega \), gegeben
Spannungsquelle: \( v(t) = V_0 cos(\omega t) \) , \( \omega = 2 \pi f \) und \( f \) ist die Frequenz.

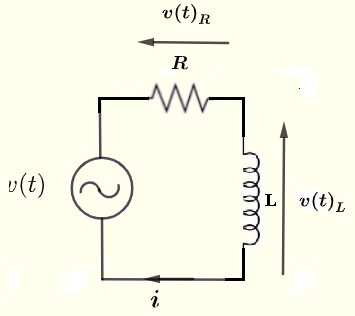
Lösung zu Beispiel 1
Sei \( V \) die komplexe Form der Spannungsquelle \( v(t) \).
Sei \( V_R \) die komplexe Form der Spannung \( v(t)_R\) über den Widerstand R.
Sei \( V_L \) die komplexe Form der Spannung \( v(t)_L\) über die Induktivität L
Sei \( I \) die komplexe Form des Stroms \( i \) durch den Widerstand und den Kondensator im gegebenen Stromkreis.
Sei die komplexe Impedanz eines Widerstands \( Z_R = R \) und die einer Induktivität \(Z_L = j \omega L \) (siehe Teil H oben).
Zeichnen Sie den Stromkreis mit den oben definierten komplexen Größen neu und wenden Sie Ohmsches und Kirchhoffsches Gesetz an.

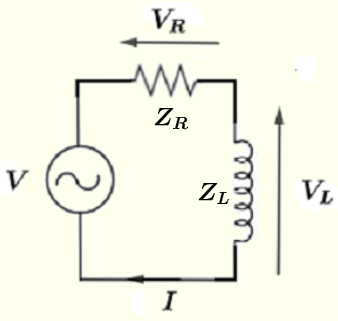
Unter Anwendung des Kirchhoffschen Gesetzes auf die Schleife des Stromkreises erhalten wir:
\( V = V_R + V_L \)         (I)
Verwenden Sie das Ohmsche Gesetz, um \( V_R \) und \( V_L \) wie folgt umzuformulieren:
\( V_R = Z_R I \)
\( V_L = Z_L I \)
Ersetzen Sie in Gleichung (I):
\( V = Z_R I + Z_L I = R I + j \omega L I = I(R + j \omega L ) \)
Lösen Sie das obige nach \( I \) auf:
\( I = \dfrac{V}{R+j \omega L} \)         (II)
Der Nenner \( R+j \omega L \) ist eine komplexe Zahl, die in komplexer Form geschrieben werden kann als:
\( R+j \omega L = r e^{j\theta} \)
wobei:
\( r = |Z| = \sqrt {R^2 + (L\omega)^2} \) das Modul ist
\( \theta = \arctan \left(\dfrac{\omega L}{R} \right) \) das Argument ist, wie im komplexen Bereich unten dargestellt.

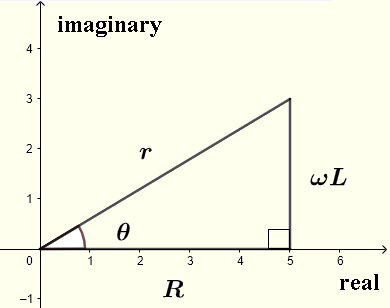
Sei \( V = V_0 e^{j\omega t} \)
Ersetzen Sie \( V \) und \( R+j \omega L \) durch ihre komplexen Formen in (II) und schreiben Sie:
\( I = \dfrac{V_0 e^{j\omega t}}{r e^{j\theta}} \)
Verwenden Sie Exponentialregeln, um das oben Gesagte zu vereinfachen:
\( I = \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
Verwenden Sie das Ohmsche Gesetz, um zu schreiben:
\( V_R = R I = \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)

\( V_L = Z_L I = \dfrac{j V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
Schreiben Sie \( j \) in exponentieller Form \( j = e^{j \pi/2} \) in \( V_L \) um:
\( V_L = \dfrac{ e^{j \pi/2} V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
Verwenden Sie die Exponentialregel, um das oben Gesagte umzuschreiben:
\( V_L = \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t + \pi/2 -\theta)} \)
Wir verwenden nun die oben berechneten komplexen Größen, um \( i \), \( v(t)_R \) und \( v(t)_L \) zu berechnen, indem wir die Realteile wie folgt nehmen:
\( i = \Re e I = \Re e \left( \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \right) \)
was ergibt:
\[ i = \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t-\theta) \] \( v(t)_R = \Re e V_R = \Re e \left( \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \right) \) \[ v(t)_R = \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t-\theta) \] \( v(t)_L = \Re e V_L = \Re e \left( \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t + \pi/2 -\theta)} \right) \) \[ v(t)_L = \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t + \pi/2 -\theta) \]

Weitere Referenzen und Links