Resolver Problemas de Circuitos de Corriente Alterna con Soluciones

Tabla de Contenidos

Las leyes de Kirchhoff y Ohm se extienden y utilizan para resolver problemas de circuitos de corriente alterna utilizando impedancias en formas complejas.
Todas las cantidades como voltajes, corrientes e impedancias se representan mediante números complejos en formas estándar y polares .

Revisión de Números Complejos

La unidad imaginaria se define por \( j = \sqrt {-1} \) o \( j^2 = - 1 \)
Un número complejo \( Z \) en la forma estándar \( Z = a + j b \) se puede escribir en forma polar como
\( Z = r \; \angle \; \theta \)
donde \( r \) y \( \theta \) son el módulo y argumento , de \( Z \), respectivamente y se definen por
\( r = |Z| = \sqrt {a^2 + b^2} \) y \( \theta = \arctan \left( \dfrac{b}{a} \right) \) dentro del rango \( -\pi \lt \theta \le \pi \)
Es más fácil dividir o multiplicar números complejos en forma polar
Sea \( Z_1 = r_1 \; \angle \; \theta_1 \) y \( Z_2 = r_2 \; \angle \; \theta_2 \)
\( Z_1 \cdot Z_2 = r_1 \cdot r_2 \; \angle \; \theta_1 + \theta_2 \)
\( \dfrac{Z_1}{Z_2} = \dfrac{r_1}{r_2} \; \angle \; \theta_1 - \theta_2 \)

Problemas con Soluciones

Problema 1
Encuentra la magnitud y el desplazamiento de fase (forma polar) de la corriente a través de y los voltajes a través del resistor \( R \) y el capacitor \( C \) en el circuito a continuación, dado que la fuente de voltaje \( v_i = 10 \cos (\omega t ) \) V, las resistencias \( R = 100 \; \Omega \), \( C = 0.47 \; \mu F \), frecuencia \( f = 1 \) kHz y \( \omega = 2 \pi f \).

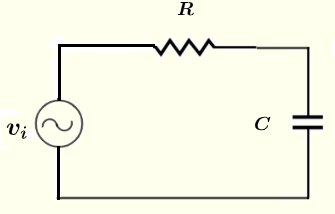
Solución al Problema 1
Sea \( V_i \), \( V_R \), \( V_C \) e \( I \) las formas complejas de \( v_i \), \( v_R \), \( v_C \) e \( i \) respectivamente.


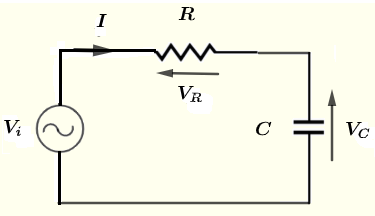
Usa la Ley de Kirchhoff del voltaje alrededor del bucle para escribir la ecuación
\( V_i - V_R - V_C = 0\)      (1)
Las impedancias complejas de la resistencia \( R \) y el condensador \( C \) están dadas por
\( Z_R = R \; \)       (real)
\( Z_C = - j \dfrac{1}{\omega C} \; \)       (imaginaria)

Usa la Ley de Ohm para escribir
\( V_R = Z_R I \) y \( V_C = Z_C I \)
Sustituye \( V_R \) y \( V_C \) por sus expresiones en la ecuación (1)
\( V_i - Z_R I - Z_C I = 0 \)
Resuelve lo anterior para \( I \)
\( I = \dfrac{V_i}{Z_R + Z_C} \)

Calcula \( V_R \) y \( V_C \) usando la Ley de Ohm de la siguiente manera
\( V_R = Z_R I = \dfrac{V_i Z_R }{Z_R + Z_C} \)

\( V_C = Z_C I = \dfrac{V_i Z_C }{Z_R + Z_C} \)


En la forma polar compleja \( v_i = 10 \cos (\omega t ) \) se puede escribir como
\( V_i = 10 \; \angle \; 0 \)

Ahora sustituimos \( V_i \), \( Z_R \) y \( Z_C \) por sus expresiones anteriores para obtener
\( I = \dfrac{10 \; \angle \; 0}{R - j \dfrac{1}{\omega C}} \)

\( V_R = \dfrac{10 R \; \angle \; 0 \; }{R - j \dfrac{1}{\omega C}} \)

\( V_C = \dfrac{ (10 \; \angle \; 0 \;) (- j \dfrac{1}{\omega C}) }{R - j \dfrac{1}{\omega C}} \)

Dejemos que el denominador de todas las expresiones anteriores sea \( Z_D = R - j \dfrac{1}{\omega C} \) y reescríbelo en forma compleja
Módulo de \( Z_D \) : \( | Z_D | = \sqrt {R^2 + \dfrac{1}{\omega^2 C^2}} \)

Argumento de \( Z_D \) : \( \phi = \arctan \dfrac{-\dfrac{1}{\omega C}}{R} = \arctan \dfrac{-1}{R \omega C} \)

Ahora reescribimos la cantidad compleja \( - j \dfrac{1}{\omega C} \) en forma polar
\( - j \dfrac{1}{\omega C} = \dfrac{1}{\omega C} \; \angle \; -\dfrac{\pi}{2} \)

Ahora sustituimos todas las cantidades complejas en \( I \), \( V_R \) y \( V_C \) por su forma polar y reescribimos
\( I = \dfrac{10 \; \angle \; 0}{{ | Z_D | \; \angle \; \phi}} \)

\( V_R = \dfrac{10 R \; \angle \; 0 \; }{ | Z_D | \; \angle \; \phi} \)

\( V_C = \dfrac{10 \; \angle \; 0 \; (\dfrac{1}{\omega C} \; \angle \; -\dfrac{\pi}{2}) }{{ | Z_D | \; \angle \; \phi}} \)

Simplifica lo anterior

\( I = \dfrac{10} { | Z_D | } \; \angle \; - \phi \)

\( V_R = \dfrac{10 R}{ | Z_D |} \; \angle \; - \phi \)

\( V_C = \dfrac{10}{ \omega C | Z_D | } \; \angle \; -\dfrac{\pi}{2}- \phi \)

Ahora sustituimos todas las cantidades conocidas por sus valores numéricos
\( \omega = 2 \cdot \pi \cdot f = 2 \cdot \pi 10^3 = 2000 \pi \)
\( | Z_D | = \sqrt {R^2 + \dfrac{1}{\omega^2 C^2}} = \sqrt {100^2 + \dfrac{1}{(2000 \pi)^2 (0.47 \cdot 10^{-6})^2}} = 353.08 \; \Omega \)
\( \phi = \arctan \dfrac{-\dfrac{1}{\omega C}}{R} = \arctan \dfrac{-\dfrac{1}{2000 \pi \cdot 0.47 \cdot 10^{-6} }}{100} = -73.55^{\circ} \)
Por lo tanto

\( I = \dfrac{10} { | Z_D | } \; \angle \; - \phi = 0.0283 \; \angle \; 73.55^{\circ} \)
La magnitud de \( I \) es \( 0.02832 \; A\) y el desplazamiento de fase es \( 73.55^{\circ} \)

\( V_R = \dfrac{10 R}{ | Z_D |} \; \angle \; - \phi = 2.832 \; \angle \; 73.55^{\circ} \)
La magnitud de \( V_R \) es \( 2.832 \; V\) y el desplazamiento de fase es \( 73.55^{\circ} \)

\( V_C = \dfrac{10}{ \omega C | Z_D | } \; \angle \; -\dfrac{\pi}{2}- \phi = 9.591 \; \angle \; -16.45^{\circ} \)
La magnitud de \( V_C \) es \( 9.591 \; V\) y el desplazamiento de fase es \( -16.45^{\circ} \)

Problema 2

Encuentra la magnitud y el desplazamiento de fase (forma polar) del voltaje \( v_o \) en el circuito a continuación, dado que la fuente de voltaje \( v_i = 10 \cos (\omega t ) \; V \), las resistencias \( R = 100 \; \Omega \), \( C = 0.47 \; \mu F \), \( L = 300 \; mH \), frecuencia \( f = 2 \) kHz y \( \omega = 2 \pi f \).


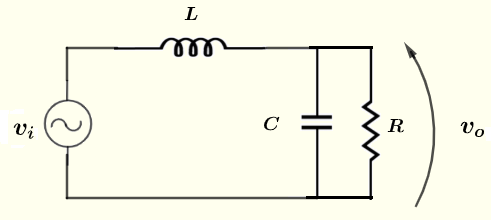
Solución al Problema 2
Sean \( I \), \( V_i \) y \( V_0 \) las formas complejas de \( i \) , \( v_i \) y \( v_o \) respectivamente.
\( V_i \) puede escribirse en forma polar de la siguiente manera
\( V_i = 10 \; \angle \; 0 \)
Las impedancias del resistor \( R \) están dadas por
\( Z_R = R \; \)
Las impedancias del condensador \( C \) están dadas por
\( Z_C = - j \dfrac{1}{\omega C} \; \)
El resistor \( R \) y el condensador \( C \) están en paralelo. La impedancia \( Z \) que es equivalente a \( R \) y \( C \) está dada por

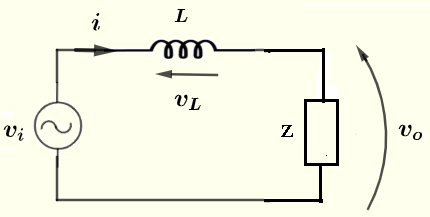
\( Z = \dfrac{Z_R \cdot Z_C}{Z_R + Z_C} \)
La bobina \( L \) tiene impedancia compleja \( Z_L \) dada por
\( Z_L = j \omega L \)
Usa la Ley de Kirchhoff del voltaje alrededor del bucle para escribir la ecuación
\( V_i - V_L - V_0 = 0\)      (1)
Usa la Ley de Ohm para escribir
\( V_L = Z_L I \) y \( V_0 = Z I \)
Sustituye \( V_L \) y \( V_0 \) por sus expresiones en la ecuación (1)
\( V_i - Z_L I - Z I = 0 \)
Resuelve para \( I \)
\( I = \dfrac{V_i}{ Z_L + Z} \)
Usa la Ley de Ohm para escribir
\( V_o = Z I = \dfrac{Z}{ Z_L + Z} V_i\)
Sustituye las cantidades conocidas para encontrar los valores numéricos
\( \omega = 2 \pi f = 2 \pi \cdot 2000 = 4000 \pi \)
\( Z_R = R = 100 \)
\( Z_C = - j \dfrac{1}{\omega C} = - j \dfrac{1}{4000 \pi \cdot 0.47 \cdot 10^{-6}} = - 169.314 j \)

\( Z = \dfrac{R \cdot Z_C}{R + Z_C} \) ( (\( R \) y \( C \) en Paralelo )

\( = \dfrac{100 \cdot (- 169.314 j)}{100 - 169.314 j } = 74.138 -43.787 j\)
y
\( Z_L = j \omega L = 4000 \pi \cdot 300 \cdot 10^{-3} j = 3769.911 j \)
\( V_o = \dfrac{Z}{ Z_L + Z} V_i \)

\( = \dfrac{Z}{ Z_L + Z} V_i \)

\( = \dfrac{74.138 -43.787 j}{ 3769.911 j + 74.138 -43.787 j} V_i \)
Simplifica
\( = (-0.01135 -0.02012 j) V_i \)
Escribe el número complejo \( (-0.01135 -0.02012 j) \) en forma polar y sustituye \(V_i \) por sus valores en forma polar dados anteriormente.
\( = ( 0.02310 \angle -119.43^{\circ} ) (10 \; \angle \; 0) \)
Simplifica
\( V_o = 0.23 \; \angle \; -119.43^{\circ} \)

Problema 3

Encuentra la magnitud y el desplazamiento de fase (forma polar) del voltaje \( v_o \) en el circuito a continuación, dado que la fuente de voltaje \( v_i = 10 \cos (\omega t ) \; V \), las resistencias \( R_1 = 220 \; \Omega \), \( R_2 = 2.2 \; k\Omega \), \( R_3 = 1 \; k\Omega \), \( C_1 = 0.47 \; \mu F \), \( C_2 = 1.5 \; \mu F \), \( L = 30\; mH \), frecuencia \( f = 2.5 \) kHz y \( \omega = 2 \pi f \).

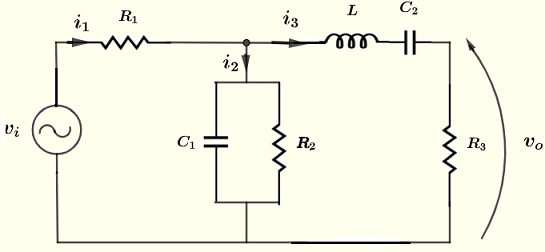
Solución al Ejemplo 3
Sean \( I_1 \), \( I_2 \), \( I_3 \), \( V_i \) y \( V_0 \) las formas complejas de \( i_1 \) , \( i_2 \), \( i_3 \) , \( v_i \) y \( v_o \) respectivamente.
\( V_i \) puede escribirse en forma polar de la siguiente manera
\( V_i = 10 \; \angle \; 0 \)
\( V_o \) puede calcularse usando la Ley de Ohm
\( V_o = R_3 I_3\)
Por lo tanto, necesitamos calcular \( I_3 \)
Agrupemos las impedancias, como se muestra en el circuito a continuación, de modo que
\( Z_1 = R_1 \)
\( Z_2 = \dfrac{R_2 ( - \dfrac{1}{\omega C_1} j)}{R_2 - \dfrac{1}{\omega C_1} j} \)      ( \( C_1 \) y \( R_2 \) están en paralelo)
\( z_3 = R_3 + j \omega L - \dfrac{1}{ \omega C_2} j \)      ( \( C_2 \), \( L \) y \( R_3 \) están en serie)

La ley de voltaje de Kirchhoff aplicada a los dos bucles cerrados da 2 ecuaciones
\( V_i - V_{z_1} - V_{z_2} = 0 \)
\( V_{z_2} - V_{z_3} = 0 \)
Aplica la Ley de Ohm para escribir \( V_{z_1} = Z_1 I_1 \), \( V_{z_2} = Z_2 I_2 \) y \( V_{z_3} = Z_3 I_3 \) y sustituye en las ecuaciones anteriores para obtener ecuaciones que solo incluyan corrientes.
\( V_i - Z_1 I_1 - Z_2 I_2 = 0 \)     (1)
\( Z_2 I_2 - Z_3 I_3 = 0 \)     (2)
Ahora usamos la ley de corriente de Kirchhoff en el nodo A para escribir
\( I_1 = I_2 + I_3 \)     (3)
Tenemos 3 ecuaciones con tres incógnitas \( I_1 \), \( I_2 \) , y \( I_3 \), pero solo necesitamos \(I_3\).
Usa la ecuación (3) para sustituir \( I_1 \) en la ecuación (1) por \( I_2 + I_3 \) y, por lo tanto, elimina \( I_1 \) de las ecuaciones y termina con un sistema de dos ecuaciones y dos incógnitas.
\( V_i - Z_1 ( I_2 + I_3) - Z_2 I_2 = 0 \)     (4)
\( Z_2 I_2 - Z_3 I_3 = 0 \)     (5)
Reescribe el sistema de ecuaciones en forma estándar
\( (Z_1 + Z_2 ) I_2 + Z_1 I_3 = V_i \)     (4)
\( Z_2 I_2 - Z_3 I_3 = 0 \)     (5)
Usa el determinante para resolver el sistema de ecuaciones anterior
\( I_3 = \dfrac{\begin{vmatrix} Z_1 + Z_2 & V_i \\ Z_2 & 0 \end{vmatrix}}{\begin{vmatrix} Z_1 + Z_2 & + Z_1 \\ Z_2 & -Z_3 \end{vmatrix}} \)
Evalúa los determinantes para encontrar
\( I_3 = \dfrac{Z_2}{(Z_1+Z_2)Z_3 + Z_1 Z_2} V_i \)

Cálculos Numéricos
\( \omega = 2 \pi f = 5000 \pi \)
\( Z_1 = 220 \)
\( Z_2 = \dfrac{2200 ( - \dfrac{1}{5000 \pi \cdot 0.47 10^{-6}} j)}{2200 - \dfrac{1}{5000 \pi \cdot 0.47 10^{-6}} j} \)

\( Z_2 = 8.30804 -134.93950 j \)

\( z_3 = 1000 + 5000 \pi \cdot 30 \cdot 10^{-3} j - \dfrac{1}{ 5000 \pi \cdot 1.5 \cdot 10^{-6}} j \)
\( Z_3 = 1000 + 428.79757 j \)
\( I_3 = (0.00013 - 0.00043 j)V_i = 0.00044 \angle -73.18^{\circ} \cdot 10 \angle 0\)
\( V_0 = R_3 I_3 = 1000 \cdot 0.00044 \angle -73.18^{\circ} \cdot 10 \angle 0 \)
Simplifica
\( V_0 = 4.4 \angle -73.18^{\circ} V \)

Más Problemas con Respuestas

Problema 4
Dado \( v_i = 10 \angle 0^{\circ} \) , \( R = 200 \; \Omega \), \( C = 0.47 \; \mu F \), \( L = 40 \; mH \) , frecuencia \( f = 1 \) kHz.
Encuentra la corriente \( I \) y el voltaje \( V_0 \) a través del inductor en formas complejas.

Respuesta al Problema 4

Respuesta: \( I = 0.047 \angle -47.84^{\circ}\) , \(V_0 = 11.38 \angle 42.16^{\circ} \)

Problema 5
Dado \( v_i = 10 \angle 0^{\circ} \) , \( R_1 = 100 \; \Omega \), \( C = 0.47 \; \mu F \), \( R_2 = 120 \; \Omega \), \( R_3 = 200 \; \Omega \), \( R_4 = 400 \; \Omega \), \( L = 20 \; mH \) , frecuencia \( f = 2 \) kHz.
Encuentra las corrientes \( I_1 \), \( I_2 \) , \( I_3 \) y los voltajes a través de cada resistor en formas complejas.

Respuesta al Problema 5
Respuestas
Corrientes: \( I_1 = 0.054 \angle 10.55^{\circ} \; , \; I_2 = 0.048 \angle 23.01^{\circ} \; , \; I_3 = 0.013 \angle -42.22^{\circ} \)
Voltajes: \( V_{R_1} = 5.49 \angle 10.55^{\circ} \; , \; V_{R_2} = 4.71 \angle -12.32^{\circ} \; , \; V_{R_3} = 2.60 \angle -42.22^{\circ} \; , \; V_{R_4} = 2.77 \angle 15.63^{\circ} \)

Más Referencias y Enlaces