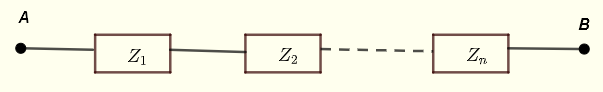
La impedancia equivalente entre los puntos A y B se da por
\[ Z_{AB} = Z_1 + Z_2 + ... + Z_n\]
Aquí se discute cómo se utilizan las impedancias complejas para calcular las impedancias equivalentes en circuitos de corriente alterna. Todos los pasos se muestran mediante cálculos simbólicos y luego se utilizan valores numéricos.
Debido a que el símbolo \( i \) se usa para corrientes en circuitos de CA, aquí usamos \( j \) como la unidad imaginaria definida por \( j^2 = -1 \) o \( j = \sqrt{-1} \)
Sea \( Z_1 \) , \( Z_2 \) ... \( Z_n \) impedancias en serie como se muestra a continuación.
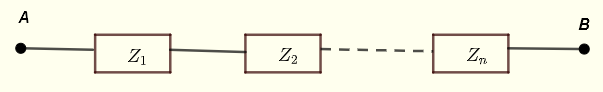
La impedancia equivalente entre los puntos A y B se da por
\[ Z_{AB} = Z_1 + Z_2 + ... + Z_n\]
Ejemplo 1
Encuentra la impedancia compleja equivalente al circuito en serie RLC mostrado a continuación, dadas las siguientes condiciones:
Frecuencia \( f = 1 \; kHz \) , \( C = 10 \; \mu F \) , \( L = 10 \; mH \) y \( R = 100 \; \Omega \)

Solución a Problemas 1
Sea
\( Z_R = R \) , \( Z_C = \dfrac{1}{j \omega C} = \dfrac{-j}{\omega C} \) , \( Z_L = j \omega L\)
Aplicamos la regla de impedancias de circuitos en serie
\( Z_{AB} = Z_R + Z_C + Z_L = R - \dfrac{j}{\omega C} + j \omega L \)
Sea
\( X_L = \omega L = 2 \pi f L \) y \( X_C = \dfrac{1}{\omega C} = \dfrac{1}{2 \pi f C} \)
y reescribimos \( Z_{AB} \) de la siguiente manera
\( Z_{AB} = R + j(X_L - X_C) \)
Sustituimos con valores numéricos
\( X_L = \omega L = 2 \pi f L = 2 \pi 10^3 10^{-2} = 62.83 \Omega \)
\( X_C = \dfrac{1}{\omega C} = \dfrac{1}{2 \pi f C} = \dfrac{1}{2 \pi 10^3 10^{-5} } = 15.92 \Omega \)
Agrupamos términos imaginarios
\( Z_{AB} = 100 + j ( 62.83 - 15.92 ) \)
Simplificamos
\( Z_{AB} = 100 + j ( 62.83 - 15.92 ) = 100 + 46.91 j\)
Escribimos lo anterior en forma exponencial
\( Z_{AB} = \sqrt {100^2 + 46.91^2} e^{j \arctan{\dfrac{46.91}{100}}} = 110.45 e^{j 0.44} \)
\( Z_{AB} \) escrito en forma de fasor
\( Z_{AB} = 110.45 \angle 0.44 \; rad = 110.45 \angle 25.13^{\circ} \)
Se puede usar un calculador de impedancia de circuito en serie RLC para más práctica.
Sea \( Z_1 \) , \( Z_2 \) ... \( Z_n \) impedancias en paralelo como se muestra a continuación.
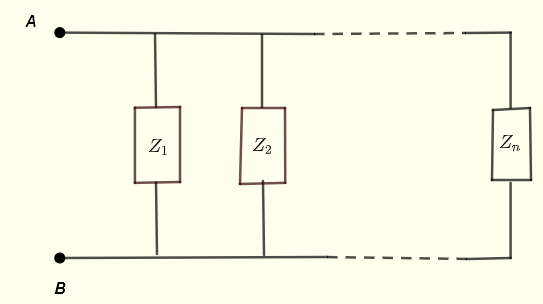
La impedancia equivalente entre los puntos A y B se da por
\[ \dfrac{1}{Z_{AB}} = \dfrac{1}{Z_1} + \dfrac{1}{Z_2} + ... + \dfrac{1}{Z_n} \]
Ejemplo 2
Encuentra la impedancia compleja equivalente al circuito en paralelo RLC mostrado a continuación, dadas las siguientes condiciones:
Frecuencia \( f = 1.5 \; kHz \) , \( C = 15 \; \mu F \) , \( L = 20 \; mH \) y \( R = 50 \; \Omega \)

Solución a Problemas 2
Sea
\( Z_R = R \) , \( Z_C = \dfrac{1}{j \omega C} \) , \( Z_L = j \omega L\)
Aplicamos la regla de impedancias de circuitos en paralelo
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{Z_R} + \dfrac{1}{Z_C} + \dfrac{1}{Z_L} \)
\( = \dfrac{1}{R} + \dfrac{1}{\dfrac{1}{j \omega C}} + \dfrac{1}{j \omega L} \)
Sea
\( X_L = \omega L \) y \( X_C = \dfrac{1}{\omega C} \)
y reescribimos lo anterior como
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{R} + \dfrac{1}{\dfrac{X_C}{j}} + \dfrac{1}{j X_L} \)
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{R} + \dfrac{j}{{X_C}} - j \dfrac{1}{ X_L} \)
\( = \dfrac{1}{R} + j (\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} ) \)
El módulo \( r \) del número complejo anterior se da por
\( r = \sqrt { (\dfrac{1}{R})^2 + (\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} )^2} \)
y su argumento \( \alpha \) se da por
\( \alpha = \arctan \left(\dfrac{\dfrac{1}{{X_C}} - \dfrac{1}{ X_L}}{\dfrac{1}{R}} \right) \)
\( = \arctan \left(\dfrac{R}{X_C}-\dfrac{R}{X_L} \right) \)
Ahora usamos la forma exponencial del número complejo para escribir
\( \dfrac{1}{Z_{AB}} = r e^{j\alpha} \)
Ahora escribimos la impedancia equivalente \( Z_{AB} \) como un número complejo en forma exponencial
\( Z_{AB} = \dfrac{1}{r} e^{-j \alpha} \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} e^{-j \arctan \left(\dfrac{R}{X_C}-\dfrac{R}{X_L} \right) } \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} e^{j \arctan \left(\dfrac{R}{X_L}-\dfrac{R}{X_C} \right) } \)
Ahora usamos los valores dados
\( f = 1.5 \; kHz \) , \( C = 15 \; \mu F \) , \( L = 20 \; mH \) y \( R = 50 \; \Omega \)
\( X_L = \omega L = 2 \pi f L = 2 \pi 1.5 \times 10^3 \times 20 10^{-3 } = 188.50 \)
\( X_C = \dfrac{1}{\omega C} = \dfrac{1}{ 2\pi f C} = \dfrac{1}{ 2\pi 1.5 \times 10^3 \times 15 10^{-6}} = 7.07\)
Módulo: \( \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{50}\right)^2 + \left(\dfrac{1}{{7.07}} - \dfrac{1}{ 188.50} \right)^2}} \)
\( = 7.27 \)
Argumento: \( \arctan \left(\dfrac{R}{X_L}-\dfrac{R}{X_C} \right) \)
\( = \arctan \left(\dfrac{50}{188.50}-\dfrac{50}{7.07} \right) \)
\( = - 81.64^{\circ} \)
Se puede usar un calculador de impedancia de circuito en paralelo RLC para más práctica.