Se presenta la definición de funciones con muchas variables y el concepto del dominio de estas funciones con ejemplos.
Problemas y sus soluciones también están incluidos.
Se necesitan habilidades en resolver sistemas de desigualdades con dos variables para encontrar el dominio de funciones con dos variables.
Consideremos algunas fórmulas muy conocidas.
a) El perímetro \( P \) de un cuadrado de lado \( x \) está dado por \( P = 4 x\).
b) El área \( A \) de un rectángulo de longitud \( L \) y ancho \( W \) está dada por \( A = L W \)
c) La fuerza \( F \), debido a la ley de gravitación universal de Newton, entre dos objetos de masas \( m_1 \) y \( m_2 \) separados por una distancia \( d \) está dada por \( F = G \dfrac{m_1 m_2}{d^2} \)
donde \( G \) es una constante.
Se puede decir que:
el perímetro \( P \) en la parte a) anterior es una función de una variable \( x \)
el área \( A \) en la parte b) anterior es una función de dos variables \( L \) y \( W \)
la fuerza \( F \) en la parte c) es una función de tres variables \( m_1 \), \( m_2 \) y \( d \) (Nota que \( G \) es una constante).
Una función \( f \) de \( n \) variables \( x_1, x_2, ...., x_n \), es una regla que asigna un número real único \( f (x_1, x_2, ...., x_n) \) a cada n-tupla de números reales \( x_1, x_2, ...., x_n \).
El conjunto \( D \) de todas las n-tuplas de números reales \( x_1, x_2, ...., x_n \) para las cuales la función \( f \) es unívocamente real se llama el dominio de la función \( f \).
Si dejamos \( u = f (x_1, x_2, ...., x_n) \), el conjunto de todos los valores de \( u \) correspondientes a todas las n-tuplas \( x_1, x_2, ...., x_n \) en \( D \) se llama el rango de \( f \) [1] , [2] , [3] .
Ejemplo 1 Función de dos Variables
Sea la función \( f \) definida por
\[ f(x,y) = \sqrt{x^2+y^2} + \ln(x-y) \]
a) Evaluar: \( f(4,3) \) , \( f(e^2,0) \)
b) Encontrar y dibujar el dominio de \( f \)
Solución al Ejemplo 1
a)
Para evaluar \( f(4,3) \), necesitamos sustituir \( x \) por \( 4 \) y \( y \) por \( 3 \)
Por lo tanto
\( f(4,3) = \sqrt{4^2+3^2} + \ln(4-3) \)
Simplificar
\( \quad = \sqrt{25} + \ln(1) = 5 + 0 = 5 \)
Para evaluar \( f(e^2,0) \), necesitamos sustituir \( x \) por \( e^2 \) y \( y \) por \( 0 \)
Por lo tanto
\( f(e^2,0) = \sqrt{e^2 + 0^2} + \ln(e^2 - 0) \)
Simplificar
\( \quad = e + 2 \)
b)
El dominio de \( f(x,y) \) se encuentra estableciendo las condiciones:
1) \( \quad x^2+y^2 \ge 0 \), una cantidad bajo la raíz cuadrada debe ser no negativa
2) \( \quad x - y \gt 0 \), el argumento de un logaritmo debe ser positivo.
La condición 1) anterior siempre se cumple.
La desigualdad en la condición 2) se puede resolver gráficamente para obtener la solución mostrada por el gráfico a continuación.

Ejemplo 2 Función de tres Variables
Sea la función \( g \) definida por
\[ g(x,y,z) = \sqrt{ x^2 + y^2 + z^2 - 9} \]
a) Evaluar: \( g(3,-1,1) \) , \( g(3/2,1/4,7/2) \)
b) Encontrar y describir el dominio de \( g \)
Solución al Ejemplo 2
a)
Para evaluar \( g(3,-1,1) \), necesitamos sustituir \( x \) por \( 3 \), \( y \) por \( -1 \) y \( z \) por \( 1 \)
Por lo tanto
\( g(3,-1,1) = \sqrt{ 3^2 + (-1)^2 + 1^2 - 9} \)
Simplificar
\( \quad = \sqrt{2} \)
Para evaluar \( g(3/2,1/4,7/2) \), necesitamos sustituir \( x \) por \( 3/2 \), \( y \) por \( 1/4 \) y \( z \) por \( 7/2 \)
Por lo tanto
\( g(3/2,1/4,2) = \sqrt{ (3/2)^2 + (1/4)^2 + (7/2)^2 - 9} \)
Simplificar
\( \quad = \dfrac{\sqrt{89}}{4} \)
b)
El dominio de \( g(x,y,z) \) se encuentra estableciendo las condiciones:
\( x^2 + y^2 + z^2 - 9 \ge 0 \), una cantidad bajo la raíz cuadrada debe ser no negativa
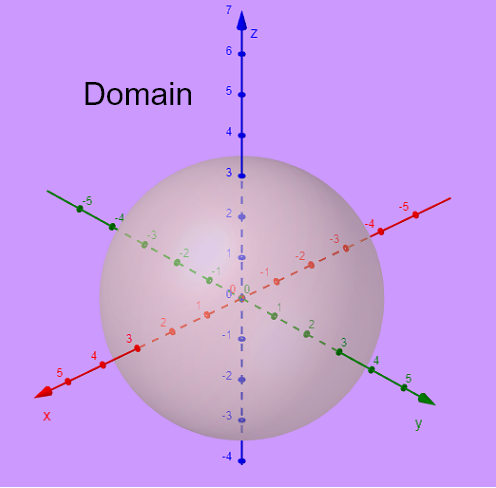
Considere \( x^2 + y^2 + z^2 - 9 = 0 \) que se puede escribir como \( x^2 + y^2 + z^2 = 3^2 \).
Por lo tanto, el gráfico de la ecuación \( x^2 + y^2 + z^2 - 9 = 0 \) es una esfera de radio \( 3 \) centrada en el origen \( (0,0,0) \) como se muestra a continuación.
Ejemplo 3 Función de dos Variables
Sea la función \( h \) definida por
\[ h(x,y) = \dfrac{1}{\ln (1 - x y) } - \sqrt{x - y^2}\]
a) Encuentra y describe el dominio de \( h \)
b) Da ejemplos de 3 pares ordenados \( (x,y) \) que estén en el dominio de \( h \) y evalúa la función en estos puntos.
c) Da ejemplos de 3 pares ordenados \( (x,y) \) que NO estén en el dominio.
Solución al Ejemplo 3
a)
El dominio de \( h(x,y) \) se encuentra estableciendo las condiciones:
1) \( \quad 1 - x y \gt 0 \) , el argumento de un logaritmo debe ser positivo
2) \( \quad x - y^2 \ge 0 \) , el argumento de la raíz cuadrada debe ser no negativo.
3) \( \quad \ln (1 - x y) \ne 0 \) o \( 1 - xy \ne 1 \) lo cual es equivalente a \( xy \ne 0 \), el denominador \( \ln (1 - x y) \) NO debe ser igual a cero.
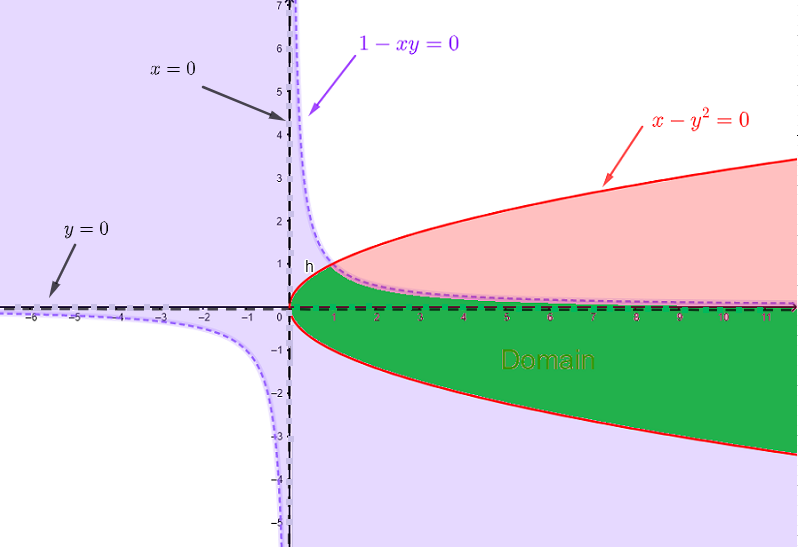
La condición 1) se resuelve graficando \( 1 - x y = 0 \) que es equivalente a \( y = \dfrac{1}{x} \) y seleccionando el conjunto de soluciones como el conjunto de puntos que satisfacen la desigualdad \( \quad 1 - x y \gt 0 \). (color morado claro)
La condición 2) se resuelve graficando \( x - y^2 = 0 \) que es equivalente a \( x = y^2 \), una parábola horizontal, y seleccionando el conjunto de soluciones como el conjunto de puntos que satisfacen la desigualdad \( \quad x - y^2 \ge 0 \). (color rojo)
La condición 3) se satisface por cualquier punto que NO esté en ninguno de los ejes. (líneas discontinuas en los ejes)
El dominio es la intersección de los tres conjuntos encontrados para las condiciones 1), 2) y 3) y se muestra a continuación en verde excluyendo cualquier punto en los ejes \( x \) o \( y \).
Parte A
Dadas las funciones:
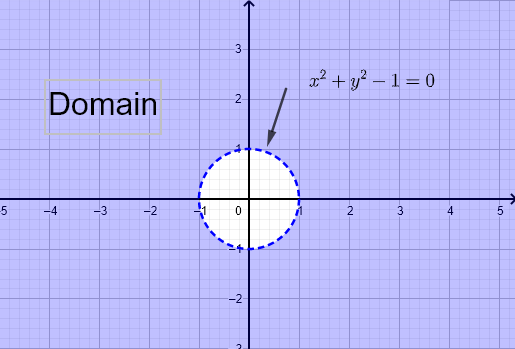
\( f (x,y) = \dfrac{1}{\sqrt{x^2 - y}} \) y \( g (x,y) = \ln (x^2 + y^2 - 1) \)
a) Encuentra el dominio de cada función
b) Evalúa
1) \( f (1,0) \) , 2) \( g (1,-1) \) , 3) \( \dfrac{f(3,4)}{g(2,0)} \)
Parte B
En un circuito eléctrico, la resistencia \( R \) de tres resistencias en paralelo y de resistencias \( r_1 , r_2 , r_3 \) están relacionadas por
\( \dfrac{1}{R} = \dfrac{1}{r_1} + \dfrac{1}{r_2} + \dfrac{1}{r_3} \)
a) Expresa \( R \) como una función de las variables \( r_1 , r_2 , r_3 \).
b) Calcula \( R \) para \( r_1 = 100 \) , \( r_2 = 50 \) y \( r_3 = 20 \).
Parte C
Encuentra el dominio de las funciones
a) \( f(x,y) = \sqrt{x^2+y-2x} \)
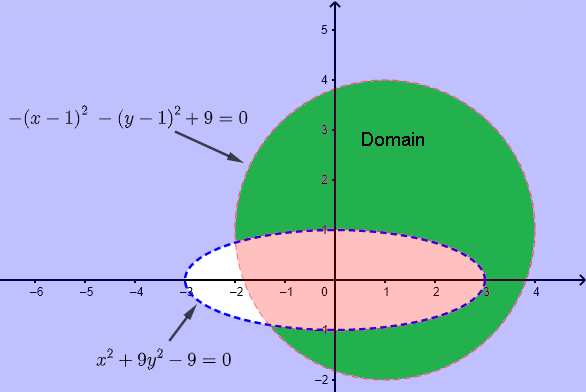
b) \( h(x,y) = \dfrac{\ln(x^2+9 y^2-9)}{\sqrt{7-x^2-y^2+2 x + 2 y}} \)
Parte A
\( f (x,y) = \dfrac{1}{\sqrt{x^2 - y}} \) y \( g (x,y) = \ln (x^2 + y^2 - 1) \)
a)
El dominio de \( f \) se encuentra resolviendo: \( x^2 - y \gt 0 \); el denominador no debe ser igual a cero y el argumento de la raíz cuadrada debe ser no negativo.
Grafica \( y = x^2 \) y selecciona el área que satisface la desigualdad \( x^2 - y \gt 0 \). La solución gráfica se muestra a continuación. El dominio es el conjunto de todos los puntos \( (x,y) \) fuera de la parábola \( y = x^2 \).

Parte B
a)
Dado \( \dfrac{1}{R} = \dfrac{1}{r_1} + \dfrac{1}{r_2} + \dfrac{1}{r_3} \),
Multiplica todos los términos de la ecuación por el producto \( r_1 r_2 r_3 \)
\( \dfrac{r_1 r_2 r_3}{R} = \dfrac{r_1 r_2 r_3}{r_1} + \dfrac{r_1 r_2 r_3}{r_2} + \dfrac{r_1 r_2 r_3}{r_3} \)
Simplifica
\( \dfrac{r_1 r_2 r_3}{R} = r_2 r_3 + r_1 r_3 + r_1 r_2 \)
Resuelve para \( R \)
\( R(r_1,r_2,r_3) = \dfrac{r_1 r_2 r_3}{r_2 r_3 + r_1 r_3 + r_1 r_2} \)
b)
\( R(100,50,20) = \dfrac{100 \times 50 \times 20}{50 \times 20 + 100 \times 20 + 100 \times 50} = 12.5\)
Parte C
a) \( f(x,y) = \sqrt{x^2+y-2x} \)
\( f(x,y) \) toma valores reales si el argumento de la raíz cuadrada es no negativo, por lo tanto, la condición
\( x^2+y-2x \ge 0 \)
Completa el cuadrado y reescribe como
\( (x-1)^2 - 1 + y \ge 0 \)
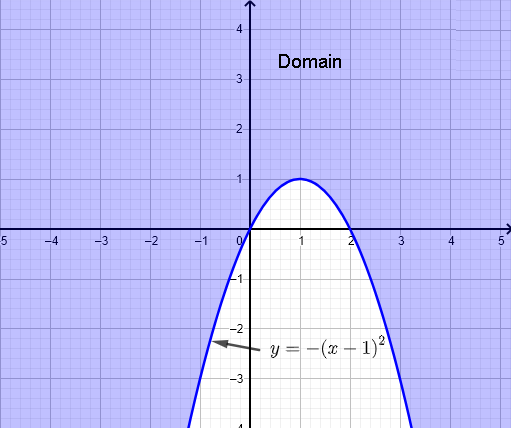
\( y \ge - (x-1)^2 + 1 \)
Grafica la parábola \( y = - (x-1)^2 + 1 \) e identifica el dominio de la función \( f \).
El dominio es el conjunto de puntos \( (x,y) \) en o fuera de la parábola \( y = - (x-1)^2 + 1 \) como se muestra en el gráfico a continuación (morado).