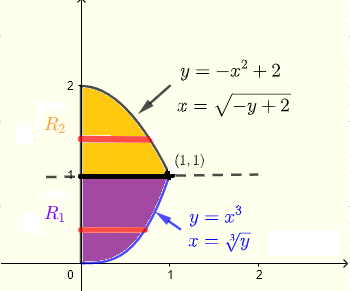Tabla de Contenidos
Integrales Dobles sobre Regiones Generales
Se presentan ejemplos para calcular y evaluar integrales dobles sobre regiones generales junto con sus soluciones detalladas.
Notas Importantes
1) Hacer gráficos y diagramas para regiones generales no rectangulares como primer paso facilita el cálculo de integrales dobles con regiones generales.
2) En general, se necesitan cuatro pasos para calcular la integral doble sobre regiones generales de integración:
PASO 1: Hacer un gráfico y/o diagrama de la región de integración
PASO 2: Decidir cómo describir la región general usando tiras verticales u horizontales y, por lo tanto, el orden de integración
PASO 3: Describir la región general de integración usando desigualdades
PASO 4: Calcular la integral
3) A continuación, describimos una región dada \( R \) de integración como un conjunto infinito de tiras verticales que permite que la integral se exprese como \( \displaystyle \iint_R f(x,y) \;dy \;dx \) o tiras horizontales que permite que la integral se exprese como \( \displaystyle \iint_R f(x,y) \;dx \;dy \)
\( \)\( \)\( \)
Cálculos de Integrales Dobles sobre Regiones Generales
Los objetivos de los ejemplos 1 y 2 es utilizar gráficos y diagramas para determinar los límites de integración para regiones generales y calcular la integral doble.
Ejemplo 1
Pregunta: Calcular la integral doble \( \displaystyle V = \iint_R (x^2+y) \;dy \;dx \) donde la región \( R \) es un triángulo en el plano \( xy\)-plano delimitado por el eje \(x\), el eje \(y\) y la recta \( y = - x + 2 \).
Solución al Ejemplo 1
Cuatro pasos principales para calcular integrales dobles con regiones generales de integración.
PASO 1 Hacer un gráfico y/o diagrama que represente la región general
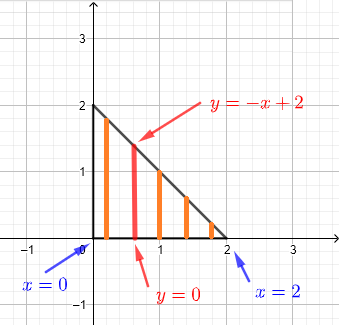
Comenzamos dibujando un gráfico o/y diagrama de la región \( R \) de integración. En este ejemplo, es un triángulo con lados en los ejes \(x\) y \(y\) y el tercer lado está descrito por la ecuación de la recta \( y = - x + 2 \).
Este triángulo también puede ser definido por tres vértices: el origen y los puntos de intersección de la recta \( y = - x + 2 \) y los ejes \(x\) y \(y\), dados por \( (2,0) \) y \( (0,2) \) respectivamente, como se muestra en el gráfico a continuación.

Hay dos formas de calcular la integral dada sobre la región dada.
PASO 2 Decidir cómo describir la región general usando tiras
1) Usamos tiras verticales para describir la región \( R \) como se muestra en el gráfico a continuación.
Suponemos que la región \( R \) se puede considerar como un conjunto infinito de tiras verticales como se muestra en el diagrama a continuación.
Cualquier tira vertical dada, en un \( x \) dado, comienza en \( y = 0 \) y termina en \( y = - x + 2 \). Dado que debemos incluir todas las tiras que describen la región \( R \), \( x \) debe tomar valores de \( x = 0 \) a \( x = 2 \). Por lo tanto, la región \( R \) de integración se puede definir como:
PASO 3 Describir la región general de integración usando desigualdades
\( R \) : \( 0 \le x \le \ 2 \) , \( 0 \le y \le - x + 2 \)
PASO 4 Calcular la integral
La integral se puede escribir como
\( \displaystyle V = \int_0^2 \int_0^{-x+2} (x^2+y) \;dy \;dx \)
\( = \displaystyle \int_0^2 ( -x^3 +\dfrac{5}{2} x^2 - 2x + 2) \;dx = 8/3\)
Respondemos ahora la misma pregunta pero usando tiras horizontales.
PASO 1 es el mismo que arriba
PASO 2 Decidir cómo describir la región general usando tiras
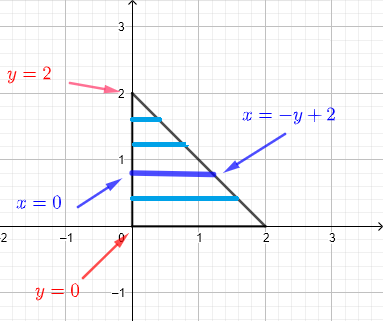
2) Usamos tiras horizontales para describir la región \( R \) como se muestra en el gráfico a continuación.
Suponemos que la región \( R \) se puede considerar como un conjunto infinito de tiras horizontales como se muestra en el diagrama a continuación.
Cualquier tira vertical dada, en un \( y \) dado, comienza en \( x = 0 \) y termina en \( x = - y + 2 \). Dado que debemos incluir todas las tiras en orden que describen la región \( R \), \( y \) debe tomar valores de \( y = 0 \) a \( y = 2 \). Por lo tanto, la región \( R \) de integración se puede definir como:
PASO 3 Describir la región general de integración usando desigualdades
\( R \) : \( 0 \le x \le - y + 2 \) , \( 0 \le y \le 2 \)
PASO 4 Calcular la integral
Por lo tanto, la integral se puede escribir como
\( \displaystyle V = \int_0^2 \int_0^{-y+2} (x^2+y) \;dx \;dy \)
\( = \displaystyle \int_0^2 (-\dfrac{1}{3} y^3 + y^2 - 2 y + \dfrac{8}{3} ) \;dy = 8/3 \)
Notas En ambos casos, la integral cuyos límites incluyen variables es la integral interna
Ejemplo 2
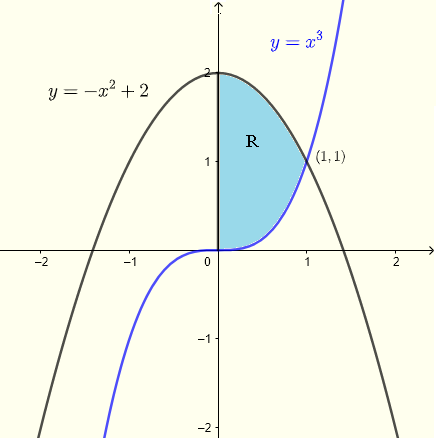
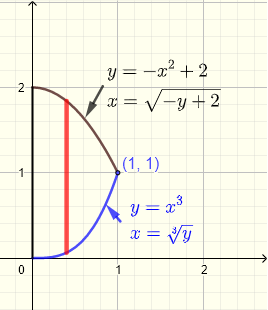
Pregunta: Calcular la integral doble \( \displaystyle V = \iint_R (x+y) \;dy \;dx \) donde la región \( R \) está en el plano \( xy\)-plano delimitada por el eje \(y\), las curvas de las ecuaciones \( y = x^3 \) y \( y = - x^2 + 2 \).
Solución del Ejemplo 2
Comenzamos analizando la región \( R \) como se muestra en el gráfico a continuación. Las dos curvas se intersecan en un punto cuya coordenada \( x \) está dada por la solución del sistema de ecuaciones
\( y = x^3 \)
\(y = - x^2 + 2 \)
Una forma de resolver el sistema anterior es restar las dos ecuaciones y simplificar para eliminar \( y \) y obtener una ecuación solo en \(x \) para obtener la ecuación
\( 0 = x^3 + x^2 - 2 \)
Con la ayuda del gráfico, es fácil ver que \( x = 1 \) es una solución al sistema anterior de ecuaciones que se puede verificar analíticamente.
La coordenada \(y\) del punto de intersección de las dos curvas se encuentra sustituyendo \( x \) por la solución ya encontrada \( 1 \) en una de las ecuaciones de las curvas para encontrar \( y = (1)^3 = 1 \).
Por lo tanto, el punto de intersección está dado por \( (1,1) \)
1) Usando tiras verticales
Una tira vertical dada comienza en la curva \( y = x^3 \) y termina en la curva \( x = - x^2 + 2 \). Para toda la región, \( x \) debe tomar todos los valores desde \( x = 0 \) hasta \( x = 1 \). Por lo tanto, la región \( R \) de integración está dada por
\( R \) : \( 0 \le x \le 1 \) , \( x^3 \le y \le - x^2 + 2 \)
Por lo tanto, la integral se puede calcular de la siguiente manera
\( \displaystyle V = \int_0^1 \int_{x^3}^{-x^2+2} (x+y) \;dy \;dx = \dfrac{803}{420}\)
2) Usando tiras horizontales
Una tira horizontal dada comienza en el eje \(y\) \( x = 0 \) y termina en la curva \( x = \sqrt[3]y \) o la curva \( x = \sqrt{- y+ 2} \). Debido a las dos curvas diferentes, la región \( R \) puede dividirse en dos regiones \( R_1 \) y \( R_2 \).
Para la región \( R_1 \), \( y \) debe tomar todos los valores desde \( y = 0 \) hasta \( y = 1 \) y para la región \( R_2 \), \( y \) debe tomar todos los valores desde \( y = 1 \) hasta \( y = 2 \).
Por lo tanto, la región \( R \) de integración tiene dos partes:
\( R_1 \) : \( 0 \le x \le \sqrt[3]y \) , \( 0 \le y \le 1 \)
y
\( R_2 \) : \( 0 \le x \le \sqrt{- y+ 2} \) , \( 0 \le y \le 1 \)
Por lo tanto, la integral se puede calcular de la siguiente manera
\( \displaystyle V = \iint_{R_1} (x+y) \;dx \;dy + \iint_{R_2} (x+y) \;dx \;dy \)
\( \displaystyle = \int_0^1 \int_{0}^{\sqrt[3]y} (x+y) \;dx \;dy + \int_1^2 \int_{0}^{\sqrt{-y+2}} (x+y) \;dx \;dy = \dfrac{803}{420}\)
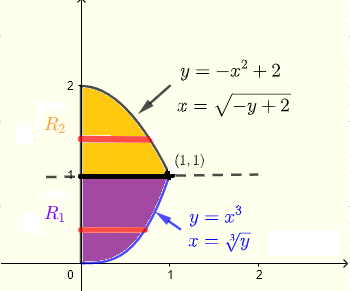
Ejemplos donde la Elección del Orden de Integración Depende del Problema Dado
En los ejemplos 3, 4 y 5, mostramos que a veces no tenemos las dos opciones del orden de integración que usualmente tenemos en las integrales dobles.
Los objetivos de los ejemplos 3, 4 y 5 son utilizar gráficos y diagramas para determinar el orden de integración que conduzca al cálculo analítico de la integral doble.
Ejemplo 3
Pregunta: Evaluar la integral doble \( \displaystyle V = \int _0^1 \int _y^1 (y + e^{-x^2}) dx dy \) si es posible. Invierta el orden de integración si es necesario para evaluar la integral dada.
Solución del Ejemplo 3
Comencemos con la integral interna
Sea
\( \displaystyle I = \int _y^1 (y+e^{-x^2}) dx \)
Al intentar evaluar \( I \) anteriormente, la integral \( \displaystyle I = \int _y^1 (e^{-x^2}) dx \) no se puede hacer analíticamente.
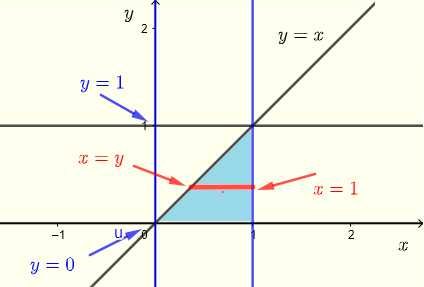
De acuerdo con los límites de integración dados, la región \( R \) de integración de la integral \( V \) se puede escribir como
\( R \) : \( y \le x \le 1 \) , \( 0 \le y \le 1 \)
con el gráfico mostrado a continuación como un conjunto de tiras horizontales.
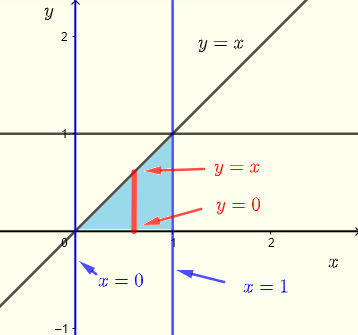
Ahora usemos tiras verticales para describir la región \( R \) como se muestra en el gráfico a continuación.
\
Grafique la región \( R \) de integración para ver si al cambiar el orden de integración, podemos proceder más adelante.
\( R \) : \( 0 \le x \le 1 \) , \( 0 \le y \le x \)
La integral \( V \) se puede escribir como
\( \displaystyle V = \int _0^1 \int _0^x (y + e^{-x^2}) dy dx \)
Evalúe usando la integral interna \( I \) dada por
\( \displaystyle I = \int _0^x (y + e^{-x^2}) dy \)
\( = \left[ \dfrac{y^2}{2} + y e^{-x^2} \right]_0^x \)
\( = \dfrac{x^2}{2} + x e^{-x^2} \)
Ahora sustituimos \( I \) en \( V \) y calculamos la integral dada
\( \displaystyle V = \int _0^1 (\dfrac{x^2}{2} + x e^{-x^2} ) dx \)
\( = \left[ \frac{x^3}{6}-\frac{1}{2}e^{-x^2} \right]_0^1 \)
\( = \dfrac{2}{3} - \dfrac{1}{2}e^{-1} \)
Ejemplo 4
Evaluar la integral doble \( \displaystyle V = \iint_R \left(\sqrt{1+y^3}+\:x\right)\:dy \:dx \) sobre la región \( R \) sombreada en rojo como se muestra a continuación.
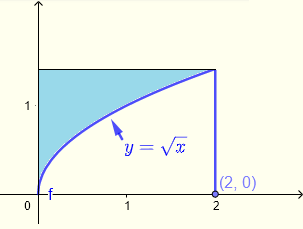
Solución del Ejemplo 4
Sea la integral interna \( \displaystyle I = \int \left(\sqrt{1+y^3}+\:x\right) \; dy \)
Es fácil ver que esta integral no es fácil de calcular analíticamente.
Intercambiemos el orden de integración.
\( V = \displaystyle \iint_R \left(\sqrt{1+y^3}+\:x\right)\:dx \:dy \)
La región \( R \) puede describirse como:
\( R\) : \( 0 \le x \le y^2 \) , \( 0 \le y \le \sqrt 2 \)
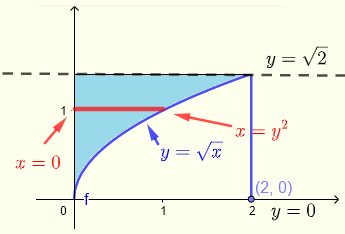
\( \displaystyle V = \int _0^{\sqrt 2} \int _0^{y^2} \left(\sqrt{1+y^3}+\:x\right) dx dy \)
Evaluemos la integral interna \( I \).
\( I = \displaystyle \int _0^{y^2} \left(\sqrt{1+y^3}+\:x\right) dx \)
\( = \left [ x \sqrt{1+y^3} + \dfrac{x^2}{2} \right]_0^{y^2} \)
Evaluamos y simplificamos
\( = y^2\sqrt{y^3+1}+\frac{y^4}{2} \)
Sustituimos \( I \) en \( V \) y calculamos la integral externa
\( \displaystyle V = \int _{0\:}^{\sqrt 2} \left(y^2\sqrt{y^3+1}+\frac{y^4}{2} \right) \; dy \)
Calculamos la integral anterior
\( \displaystyle V = \left [ \frac{2}{9}\left(y^3+1\right)^{\frac{3}{2}}+\frac{y^5}{10} \right]_0^{\sqrt 2} \)
Simplificamos
\( V = \frac{2}{9}\left(\left(\sqrt{2}\right)^3+1\right)^{\frac{3}{2}}+\frac{\left(\sqrt{2}\right)^5}{10}-\dfrac{2}{9} \approx 2.00 \)
Ejemplo 5
Evaluar la integral doble \( \displaystyle V = \iint_R (x+y)\:dydx \) sobre la región \( R \) delimitada por las curvas de las ecuaciones \( x = (y-2)^2-2 \) y \( y = - x + 6 \)
Solución del Ejemplo 5
Si se usan tiras verticales, la región de integración tendrá dos partes porque los límites de \( y \) son diferentes en los intervalos \( -2 \le x \le 2 \) y \( 2 \le x \le 7 \) y los cálculos de la integral son muy desafiantes.
Por lo tanto, usamos tiras horizontales.
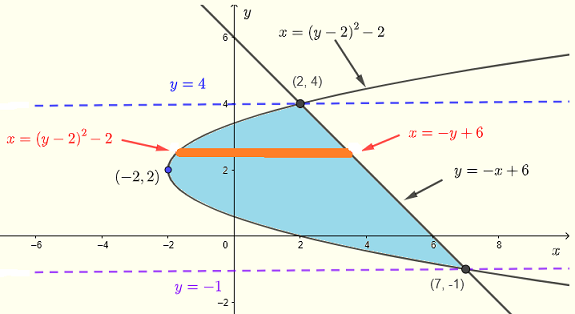
La región \( R \) puede describirse como:
\( R\) : \( (y-2)^2 - 2 \le x \le -y+6 \) , \( -1 \le y \le 4 \)
\( \displaystyle V = \int _{-1}^{4} \int _{(y-2)^2 - 2}^{-y+6} (x+y)\:dx \: dy \)
Sea la integral interna \( \displaystyle I = \int _{(y-2)^2 - 2}^{-y+6} (x+y)\:dx \)
Calculamos la integral anterior
\( I = \dfrac{-y^4+6y^3-13y^2+12y+32}{2} \)
Sustituimos \( I \) en \( V \) y calculamos la integral externa
\( \displaystyle V = \int _{-1}^4 \left( \dfrac{-y^4+6y^3-13y^2+12y+32}{2} \right) \; dy \)
Calculamos la integral anterior
\( \displaystyle V = \dfrac{1}{2} \left[-\dfrac{y^5}{5}+\dfrac{3y^4}{2}-\dfrac{13y^3}{3}+6y^2+32y\right]_{-1}^4 \)
Evaluamos
\( V = \dfrac{875}{12} \)
Nota
Como ejercicio, demuestra que usando tiras verticales, la integral doble está dada por:
\( \displaystyle \int _{-2}^2\:\int _{2-\sqrt{x+2}}^{2+\sqrt{x+2}}\:\left(x+y\right)dydx+\int _2^7\:\int _{2-\sqrt{x+2}}^{-x+6}\:\left(x+y\right)dydx \)
Más preguntas con respuestas
Parte 1
-
Escribe los límites de la integral doble \( \displaystyle V = \iint_R x y \;dy \;dx \) y \( \displaystyle V = \iint_R x y \;dx \;dy \) donde la región \( R \) está en el plano \( xy\) tal que \(x \ge 0\) y \(y \ge 0\) y está limitada por la curva cuya ecuación es
\( x^2 + y^2 = 1 \) y evalúala.
-
Escribe los límites de la integral doble \( \displaystyle V = \iint_R \sin(x^2) \;dy \;dx \) y \( \displaystyle V = \iint_R \sin(x^2) \;dx \;dy \) donde la región \( R \) es un triángulo con vértices en los puntos \( A(0,0)\) , \( B(3,0) \) y \( C(3,3) \) y evalúala.
Parte 2
Evalúa \( \displaystyle V = \int _0^1 \int _{ \arcsin y}^{\frac{\pi }{2}}\:\left(xy\right)dxdy \)
Respuestas a las preguntas anteriores
Parte 1:
-
Región de integración
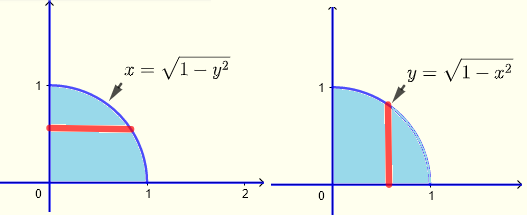
Tiras verticales
\( 0 \le x \le 1 \) , \( 0 \le y \le \sqrt{1-x^2} \)
\( \displaystyle \int _0^1\:\int _0^{\sqrt{1-x^2}}\:xy\:dy\:dx = 1/8 \)
Tiras horizontales
\( 0 \le x \le \sqrt{1-y^2} \) , \( 0 \le y \le 1 \)
\( \displaystyle \int _0^1\:\int _0^{\sqrt{1-y^2}}\:xy\:dx\:dy = 1/8\)
-
Región de integración

Tiras verticales
\( 0 \le x \le 3\) , \( 0 \le y \le x \)
\( \displaystyle \int _0^3\:\int _0^x \:\sin(x^2)\:dy\:dx = \dfrac{1}{2}\left(-\cos \left(9\right)+1\right) \)
Tiras horizontales
\( y \le x \le 3 \) , \( 0 \le y \le 3 \)
\( \displaystyle \int _y^3\:\int _0^3\:\sin(x^2)\:dx\:dy \) Muy difícil de resolver analíticamente.
Parte 2
\( \displaystyle V = \int _0^1 \int _{ \arcsin y}^{\frac{\pi }{2}}\:\left(xy\right)dxdy \)
Calcula la integral interna \( I \) dada por
\( \displaystyle I = \int _{ \arcsin y}^{\frac{\pi }{2}}\:\left(xy\right)dx \)
\( = y \left(\dfrac{\pi^2}{8} - \dfrac{\arcsin^2(y)}{2} \right) \)
Ahora sustituimos \( I \) por su expresión en la integral \( V \)
\( \displaystyle V = \int _0^1 (y \left(\dfrac{\pi^2}{8} - \dfrac{\arcsin^2(y)}{2} \right)) dy \)
lo cual es desafiante de hacer analíticamente.
Reiniciemos y ahora intercambiemos el orden de integración
Primero grafiquemos la región \( R \) de integración
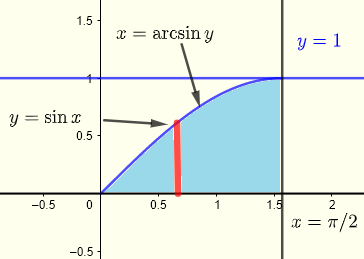
\( \displaystyle V = \int _0^{\frac{\pi }{2}} \int _0^{\sin x} x \; y \; dy \;dx \)
Sea la integral interna \( I = \int _0^{\sin x} x \; y \; dy \)
Calcula \( I \)
\( I = x\frac{\sin ^2\left(x\right)}{2} \)
\( \sin^2(x) = \dfrac{1-\cos(2x)}{2} \)
\( I = \dfrac{x}{4}(1-cos(2x) \)
Sustituye \( I \) en \( V \)
\( \displaystyle V = \int _0^{\frac{\pi }{2}} (\dfrac {x}{4} - \dfrac {x}{4} \cos (2x) ) dx \)
Divide el integrando
\( \displaystyle = \int _0^{\frac{\pi }{2}} \dfrac {x}{4} dx - \int _0^{\frac{\pi }{2}} \dfrac {x}{4} \cos (2x) dx \)
La integral a la derecha se resuelve usando la técnica de integración por partes para obtener
\( = \left[ \frac{x^2}{8} \right]_0^{\pi/2}- \left[\frac{1}{8} x \sin (2x)+\frac{1}{16}\cos (2x) \right]_0^{\pi/2} \)
Evalúa
\( = \dfrac{\pi^2+4}{32} \)
Más referencias y enlaces
- Cálculos de Integrales Dobles
- Howard Anton, Irl C. Bivens, Stephen Davis ; Cálculo: Trascendentes Tempranas; Willey, 2012.
- Gilbert Strang; MIT, Cálculo, Wellesley-Cambridge Press, 1991
- Joel Hass, Universidad de California, Davis; Maurice D. Weir Naval Postgraduate School; George B. Thomas, Jr.Massachusetts Institute of Technology ; Cálculo Universitario , Trascendentes Tempranas, Tercera Edición
, Boston Columbus , 2016, Pearson.
Matemáticas para Ingenieros con Ejemplos y Soluciones