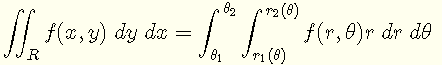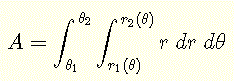Tabla de Contenidos
Integrales Dobles en Coordenadas Polares
Se presentan ejemplos sobre cómo calcular integrales dobles en coordenadas polares y regiones generales de integración junto con sus soluciones detalladas. Los ejemplos también muestran que convertir integrales dobles de coordenadas rectangulares a polares puede hacer que sea menos desafiante evaluarlas usando funciones elementales.
Convertir Integrales Dobles en Coordenadas Polares
El cambio de integrales dobles de coordenadas cartesianas (o rectangulares) a coordenadas polares se da por [1]
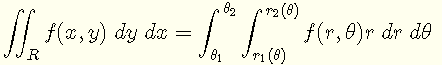
con las relaciones entre las coordenadas rectangulares x y y; y las coordenadas polares r y θ dadas por [6]
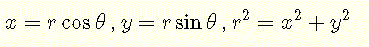
El área A de una región cerrada R descrita en coordenadas polares está dada por
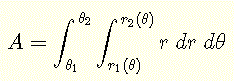
Ejemplos con Soluciones Detalladas
Ejemplo 1
\( \) \( \) \( \) \( \)
Pregunta: Calcula la integral doble \( \displaystyle V = \iint_R \sqrt {1 - x^2 - y^2} \;dy \;dx \) donde la región \( R \) es la superficie encerrada por un círculo en el plano \( xy \) con centro en el origen y radio igual a \( 1\).
Solución al Ejemplo 1
La integral dada está en coordenadas rectangulares y no se puede calcular utilizando funciones elementales. Intentemos convertirla a coordenadas polares.
Sea \( f(x,y) = \sqrt {1 - x^2 - y^2} \) y expresemos en coordenadas polares.
-example-1.gif)
\( r^2 = x^2 + y^2 \)
Por lo tanto, la función \( f(x,y) \) en forma polar está dada por
\( f(r,\theta) = \sqrt {1 - r^2} \)
La región \( R \) de integración es un círculo y puede ser definida por desigualdades de la siguiente manera:
\( R: \) \( 0 \le \theta \le 2\pi \) y \( 0 \le r \le 1 \)
La integral dada en coordenadas rectangulares puede convertirse a coordenadas polares de la siguiente manera
\( \displaystyle V = \iint_R \sqrt {1 - x^2 - y^2} \;dy \;dx = \int_0^{2\pi} \int_0^{1} \sqrt{1-r^2} \; r \; dr \; d\theta \)
Sea \( I \) la integral interna definida por
\( \displaystyle I = \int_0^{1} \sqrt{1-r^2} \; r \; dr \)
\( = \left[ -\frac{1}{3}\left(1-r^2\right)^{\frac{3}{2}} \right]_0^1 = \dfrac{1}{3} \)
Sustituye \( I \) y calcula \( V \)
\( \displaystyle V = \int_0^{2\pi} (1/3) \; d\theta \)
\( = \dfrac{1}{3} \left[ \theta \right]_0^{2\pi} \)
\( = \dfrac{2\pi}{3} \)
Ejemplo 2
Pregunta: Calcular la integral doble \( \displaystyle V = \int_0^{1} \int_0^{\sqrt{1-x^2}} e^{x^2+y^2} \; dy \; dx \)
Solución al Ejemplo 2
La integral dada no puede calcularse fácilmente en coordenadas rectangulares, por lo que necesitamos usar coordenadas polares en su lugar, lo que puede facilitar la evaluación.
Expresamos \( f(x,y) = e^{x^2+y^2} \) en coordenadas polares.
\( r^2 = x^2 + y^2 \)
Por lo tanto, la función \( f(x,y) \) en forma polar está dada por
\( f(r,\theta) = e^{r^2} \)
En coordenadas rectangulares, la región \( R \) de integración está definida por los límites de integración dados.
\( R: \) \( 0 \le x \le 1 \) y \( 0 \le y \le \sqrt{1-x^2} \)
Resolvamos la desigualdad \( y \le \sqrt{1-x^2} \) gráficamente
Elevamos ambos lados de la desigualdad al cuadrado
\( y^2 \le 1-x^2 \)
Reescribimos con términos en \( x \) y \( y \) en el lado izquierdo
\( y^2 + x^2 \le 1 \)
La desigualdad anterior es el conjunto de todos los puntos \( (x,y) \) dentro o en el círculo con centro en el origen \( (0,0) \) y radio \( 1 \)
Juntando todas las desigualdades, la región de integración \( R \) se muestra a continuación.

La región anterior en forma polar se muestra a continuación

y está definida por las desigualdades
\( R: \) \( 0 \le \theta \le \pi/2 \) y \( 0 \le r \le 1 \)
La integral ahora puede convertirse en coordenadas polares de la siguiente manera
\( \displaystyle V = \int_0^{1} \int_0^{\sqrt{1-x^2}} e^{x^2+y^2} \; dy \; dx = \int_0^{\pi/2} \int_0^1 e^{r^2} r \; dr \; d\theta \)
Sea \( I \) la integral interna definida por
\( \displaystyle I = \int_0^1 e^{r^2} r \; dr \)
\( = \left[ \dfrac{1}{2} e{r^2} \right]_0^1 \)
\( = \dfrac{1}{2} (e - 1) \)
Sustituye \( I \) en \( V \)
\( \displaystyle V = \int_0^{\pi/2} \dfrac{1}{2} (e - 1) \; d\theta \)
\( = \dfrac{\pi}{4} (e - 1) \)
Ejemplo 3
Pregunta: Expresar la integral \( \displaystyle V = \iint_R {x^2+y^2} \; dy \; dx \) donde \( R \) es un círculo en el plano \( xy \) con centro en el punto \( (1,0) \) y un radio igual a \( 1 \) usando coordenadas cartesianas (o rectangulares) y coordenadas polares. Evaluar la integral.
Solución al Ejemplo 3
Primero graficamos la región de integración \( R \) y la definimos en términos de coordenadas cartesianas y polares.
1) Coordenadas cartesianas
La ecuación del círculo con centro en \( (1,0) \) y radio igual a \( 1 \) está dada por
\( (x-1)^2 + y^2 = 1 \)
Expandimos y agrupamos términos similares
\( x^2 - 2x + y^2 = 0 \)
Resolvemos la ecuación anterior para \( y \) para obtener dos soluciones
\( y = \pm \sqrt {2x-x^2} \)
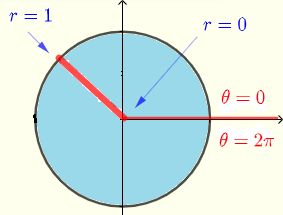
Usando tiras verticales, la región \( R \) puede describirse por las desigualdades
\( R: \) \( 0 \le x \le 2 \) y \( - \sqrt {2x-x^2} \le y \le \sqrt {2x-x^2} \)
La integral puede escribirse como
\( \displaystyle V = \int_0^2 \int_{-\sqrt {2x-x^2}}^{\sqrt {2x-x^2}} \; \; (x^2+y^2) \; dy \; dx \)
Sea \( I_1 \) la integral interna dada por
\( \displaystyle I_1 = \int_{-\sqrt {2x-x^2}}^{\sqrt {2x-x^2}} \; \; (x^2+y^2) \; dy \)
Evaluamos \( I_1 \)
\( \displaystyle I_1 = 2x^2\sqrt{2x-x^2}+2\cdot \frac{\left(2x-x^2\right)^{\frac{3}{2}}}{3} \)
El siguiente paso para calcular la integral externa anterior en coordenadas rectangulares es un desafío.
2) Coordenadas polares
Usando tiras desde el origen hasta un punto en el círculo: en el origen \( r = 0 \); en el círculo \( r = \sqrt {x^2 + y^2} \)
Convertimos la ecuación del círculo, \( x^2 + y^2 = 2x \), en forma polar.
De la relación entre coordenadas rectangulares y polares [6], tenemos
\( r^2 = x^2 + y^2 \) y \( x = r \cos \theta \)
Sustituimos \( x^2 + y^2 \) por \( r^2 \) y \( x \) por \( r \cos \theta \) en la ecuación \( x^2 + y^2 = 2x \) para obtener
\( r^2 = 2 r \cos \theta \)
Dividimos ambos lados de la ecuación anterior por \( r \)
\( r = 2 \cos \theta \)
En coordenadas polares, la región \( R \) puede describirse por las desigualdades
\( R: \) \( -\pi/2 \le \theta \le \pi/2 \) y \( 0 \le r \le 2 \cos \theta \)

Usamos \( r^2 = x^2 + y^2 \)
para escribir la integral en forma polar como
\( \displaystyle V = \int_{-\pi/2}^{\pi/2} \int_{0}^{2 \cos \theta} r^2 \; r \; dr \; d\theta \)
Sea la integral interna \(I \) definida por
\( \displaystyle I = \int_{0}^{2 \cos \theta} r^2 \; r \; dr \)
Evaluamos
\( \displaystyle I = \left[ r^4 / 4 \right]_{0}^{2 \cos \theta} \)
\( \displaystyle I = 4 cos^4 \theta \) (eq 1)
Reducimos la potencia en la expresión anterior \( \cos^4 \theta \)
\( \cos^4 \theta = \cos^2 \theta \cos^2 \theta \)
Usamos la identidad de reducción de potencia
\( \cos^2 \theta = \dfrac{cos (2\theta) + 1}{2} \)
Por lo tanto
\( \cos^4 \theta = \left( \dfrac{\cos (2\theta) + 1}{2} \right)^2 \)
\( = \dfrac{\cos^2(2\theta) + 2 \cos (2\theta) + 1}{4} \)
Usamos la identidad de reducción de potencia una vez más para obtener
\( \cos^4 \theta = \dfrac{\cos(4\theta) + 4\cos(2\theta) }{8} + 3/8 \)
Ahora sustituimos la expresión anterior en (eq 1) para obtener
\( I = \dfrac{\cos(4\theta) + 4\cos(2\theta) }{2} + 3/2 \)
Sustituimos \( I \) en la integral y evaluamos
\( \displaystyle V = \int_{-\pi/2}^{\pi/2} (\dfrac{\cos(4\theta) + 4\cos(2\theta) }{2} + 3/2 ) \; d\theta \)
\( \displaystyle = \left[ \frac{1}{2}\left(\frac{1}{4}\sin \left(4\theta\right)+2\sin \left(2\theta\right)\right)+\frac{3}{2}\theta \right]_{-\pi/2}^{\pi/2} \)
\( = \dfrac{3\pi}{2} \)
La integral dada se evalúa mucho más fácilmente usando coordenadas polares.
Ejemplo 4
Pregunta: Cambia la integral \( \displaystyle V = \int_{-1}^0 \int_{-\sqrt{1-x^2}}^0 \dfrac{\sqrt{x^2+y^2}}{1+\sqrt{x^2+y^2}} \; dy \; dx \) a coordenadas polares y evalúala.
Solución al Ejemplo 4
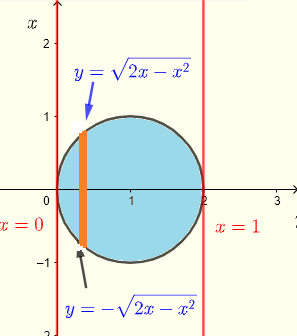
A partir de los límites de integración en coordenadas rectangulares, deducimos la región \( R \) de integración que es un cuarto de círculo en el cuadrante III como
\( R: \) \( 0 \le x \le 2 \) y \( - \sqrt {1-x^2} \le y \le 0 \)
y su gráfica se muestra a continuación
En coordenadas polares usando tiras desde el origen hasta un punto en el cuarto de círculo: en el origen \( r = 0 \). En el círculo \( r = 1 \), la región \( R \) de integración en coordenadas polares puede definirse como
\( R: \) \( \pi \le \theta \le 3\pi/2 \) y \( 0 \le r \le 1 \)
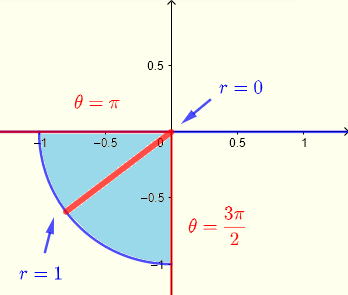
Usa \( r = \sqrt { x^2 + y^2 } \)
para escribir la integral dada en forma polar como
\( \displaystyle V = \int_{\pi}^{3\pi/2} \int_{0}^{1} \dfrac{r}{1+r} \; r \; dr \; d\theta \)
\( \displaystyle = \int_{\pi}^{3\pi/2} \int_{0}^{1} \dfrac{r^2}{1+r} \; dr \; d\theta \)
Usa división para expandir el integrando \( \dfrac{r^2}{1+r} \) como sigue
\( \dfrac{r^2}{1+r} = r-1+\frac{1}{r+1} \)
Sustituye el integrando en forma expandida en la integral
\( \displaystyle V = \int_{\pi}^{3\pi/2} \int_{0}^{1} (r-1+\frac{1}{r+1}) \; dr \; d\theta \)
Integra
\( \displaystyle = \int_{\pi}^{3\pi/2} \left[ \dfrac{r^2}{2} - r + ln |r+1| \right]_0^1 d\theta \)
Evalúa
\( \displaystyle = \int_{\pi}^{3\pi/2} (\ln (2)-\dfrac{1}{2}) d\theta \)
Integra
\( = \left( \ln (2)-\dfrac{1}{2} \right) \left[ \; \theta \; \right]_{\pi}^{3\pi/2} \)
Evalúa
\( V = \dfrac{\pi}{2} \left( \ln (2)-\dfrac{1}{2} \right) \)
Más Preguntas con Respuestas
Parte 1
Convierte cada integral a coordenadas polares y evalúala.
-
\( \displaystyle V = \int_{-1}^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \; \; \sin(x^2+y^2) \;dy \;dx \)
-
\( \displaystyle V = \int _0^2\:\:\int _0^{\sqrt{4-x^2}} \sqrt{x^2+y^2} \:\;dy\:\;dx\: \)
Parte 2
-
Evalúa \( \displaystyle V = \iint_R \: e^{\sqrt{x^2+y^2}} \; dx \; dy \) donde \( R \) es la región (azul) mostrada en el diagrama a continuación.
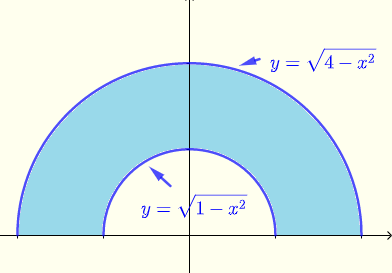
Respuestas a las Preguntas Anteriores
Parte 1:
-
La región de integración en coordenadas rectangulares (lado izquierdo) dada por los límites de integración y en coordenadas polares (lado derecho) se muestra a continuación.

\( \displaystyle V = \int_{-1}^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \; \; \sin(x^2+y^2) \;dy \;dx \)
Convierte la integral anterior a coordenadas polares
\( \displaystyle V = \int_{0}^{2\pi} \int_0^1 \; \; \sin(r^2) \;r \; dr \;d\theta \)
Evalúa
\( = \pi (1 -\cos 1) \)
-
La región de integración en coordenadas rectangulares (lado izquierdo) dada por los límites de integración y en coordenadas polares (lado derecho) se muestra a continuación.
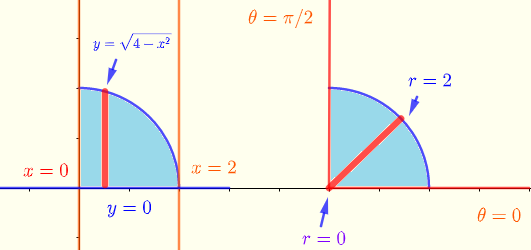
\( \displaystyle V = \int _0^2\:\:\int _0^{\sqrt{4-x^2}} \sqrt{x^2+y^2} \:\;dy\:\;dx\: \)
Convierte la integral anterior a coordenadas polares
\( \displaystyle V = \int_{0}^{\pi/2} \int_0^2 \; \; r^2 \; dr \;d\theta \)
Evalúa
\( = \dfrac{4\pi }{3} \)
Parte 2
Evalúa la integral dada usando coordenadas rectangulares
\( \displaystyle V = \int_{-2}^{2} \int_0^{\sqrt{4-x^2}} \: e^{\sqrt{x^2+y^2}} \; dy \; dx - \int_{-1}^{1} \int_0^{\sqrt{1-x^2}} \: e^{\sqrt{x^2+y^2}} \; dy \; dx \)
lo cual es bastante desafiante usando funciones elementales.
La región de integración en coordenadas polares se muestra a continuación
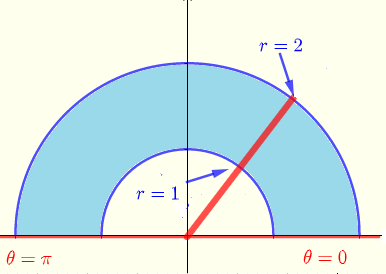
\( R: \) \( 0 \le \theta \le \pi \) y \( 1 \le r \le 2 \)
Dado
\( \displaystyle V = \iint_R \: e^{\sqrt{x^2+y^2}} \; dx \; dy \)
La integral dada en coordenadas polares es
\( \displaystyle V = \int_0^{\pi} \; \int_1^2 \: r e^{r} \; dr \; d\theta \)
Evalúa
\( = \pi e^2 \)
Más Referencias y Enlaces
- Joel Hass, Universidad de California, Davis; Maurice D. Weir Escuela de Posgrado Naval; George B. Thomas, Jr.Cálculo Universitario , Transcendentales Tempranas, Tercera Edición
, Boston Columbus , 2016, Pearson.
- Cálculos de Integrales Dobles
Integrales Dobles sobre Regiones Generales
- Howard Anton, Irl C. Bivens, Stephen Davis ; Cálculo: Transcendentales Tempranos; Willey, 2012.
- Gilbert Strang; MIT, Cálculo, Wellesley-Cambridge Press, 1991
- coordenadas polares
- Convertir Coordenadas Polares a Rectangulares y Viceversa
Matemáticas para Ingenieros con Ejemplos y Soluciones
-example-1.gif)