Circuito Resonante Serie RLC

Tabla de Contenidos

Resonante circuitos serie RLC y fórmulas de la frecuencia resonante, las frecuencias de corte están desarrolladas, el ancho de banda y el factor de calidad están definidos y se utilizan en ejemplos con soluciones detalladas. \( \) \( \) \( \) \( \)
En lo que sigue, la letra mayúscula \( I \) es la forma compleja (polar) de la corriente real \( i \) y la letra mayúscula \( V_i \) es la forma compleja (polar) del voltaje real \( v_i \).
Se puede utilizar una calculadora de circuitos resonantes serie RLC para verificar los cálculos de los ejemplos a continuación y también para obtener más práctica e investigar sobre estos circuitos.

A - Circuito resonante serie RLC

Considere el circuito serie RLC que se muestra a continuación.

Para un circuito alimentado por una fuente de voltaje de frecuencia \( f \), la impedancia total \( Z \) del circuito serie RLC se da por:
\[ Z = R + j \left(\omega L - \dfrac{1}{\omega C} \right) \]
La relación entre la corriente \( I \) y el voltaje \( V_i \) se da por
\[ I = \dfrac{V_i}{Z} \]
donde \( V_i \) e \( I \) son la forma compleja del voltaje \( v_i \) y la corriente \( i \) respectivamente.
Utilizando la definición de la magnitud de un número complejo, la magnitud \( |Z| \) se da por
\( |Z| = \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} \)
Si \( V_0 \) es el valor pico de la fuente de voltaje \( v_i = V_0 \cos (\omega t) \), entonces el valor pico \( I_0 \) de \( I \) se da por
\( I_0 = \dfrac{V_0}{ |Z| } = \dfrac{V_0}{ \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} } \)
La frecuencia de resonancia se define como la frecuencia para la cual \( I_0 \) es máximo o cuando la magnitud de \( Z \) es mínima.
Dado que la resistencia \( R \) es independiente de la frecuencia, el valor mínimo de \( |Z| \) ocurre en \( \omega = \omega_r \) tal que
\( \left(\omega_r L - \dfrac{1}{\omega_r C} \right) = 0 \)
Resuelva lo anterior para \( \omega_r \) para obtener la frecuencia resonante
\[ \omega_r = \dfrac{1}{\sqrt {L C}} \quad \quad (I) \]
En la frecuencia resonante \( \omega = \omega_r \), tenemos:
1) \( Z = R \)
Para \( V_0 \), el valor pico de la fuente de voltaje \( v_i \), el valor pico \( I_0 \) de \( I \) se da por
2) \( I_0 = \dfrac{V_0}{R} \)
Defina \( X_L = \omega L \) y \( X_C = \dfrac{1}{\omega C} \)
3) \( X_L = X_C \)

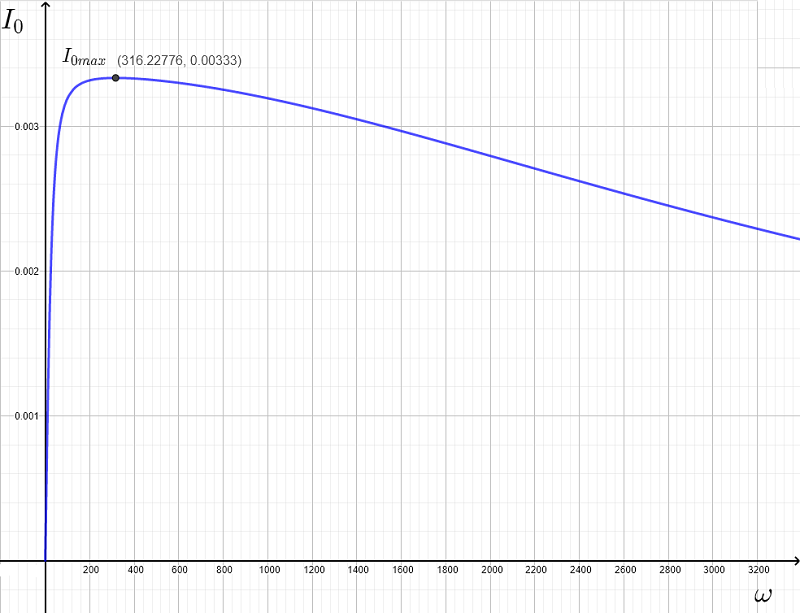
B - Potencia Promedio en un Circuito Resonante

La potencia promedio \( P_a \) entregada al circuito serie RLC se da por: \[ \displaystyle \quad \quad P_a = \dfrac{V_0^2}{2 |Z|} \cos \theta \quad \quad (II) \] donde \( \theta \) es el argumento de la impedancia \( Z = R + j \left(\omega L - \dfrac{1}{\omega C} \right) \) y se da por
\( \theta = \arctan \left( \dfrac{ \omega L - \dfrac{1}{\omega C} }{R} \right) \)
Utilizando las propiedades de las funciones trigonométricas inversas, tenemos
\( \tan \theta = \left( \dfrac{ \omega L - \dfrac{1}{\omega C} }{R} \right) \)
\( \theta \) puede asumirse como un ángulo agudo de un triángulo rectángulo como se muestra a continuación. (Use la definición de la tangente de un ángulo en un triángulo rectángulo y vea que puede obtener \( \tan \theta \) como se define anteriormente.



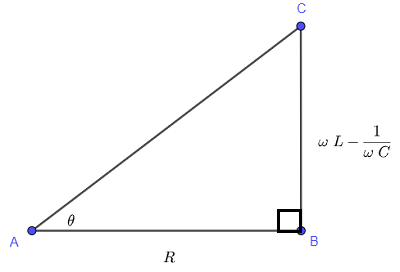
Ahora usamos el mismo triángulo y calculamos el factor de potencia \( \cos \theta \)
La hipotenusa del triángulo se calcula de la siguiente manera
\( AC = \sqrt {R^2 + \left( \omega L - \dfrac{1}{\omega C} \right)^2} \)
\( \cos \theta = \dfrac{AB}{AC} = \dfrac{R}{\sqrt {R^2 + \left( \omega L - \dfrac{1}{\omega C} \right)^2}} \)
Sustituya \( \cos \theta \) y \( |Z| \) en la fórmula (II) dada anteriormente y exprese la potencia \( P_a \) como
\( \displaystyle \quad \quad P_a = \dfrac{V_0^2}{2 \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} }\dfrac{R}{\sqrt {R^2 + \left( \omega L - \dfrac{1}{\omega C} \right)^2}} \)
Simplifique
\[ \displaystyle \quad \quad P_a = \dfrac{V_0^2 R}{2 \left({R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} \right) } \quad \quad (III) \]
En la frecuencia resonante \( \omega_r = \dfrac{1}{\sqrt {LC}} \), tenemos \( \left(\omega_r L - \dfrac{1}{\omega_r C} \right) = 0 \) y por lo tanto la potencia es máxima y es igual a \[ P_{a max} = \dfrac{V_0^2}{2 \; R} \quad \quad (IV) \]

C - Frecuencias de Corte de un Circuito Resonante y el Factor de Calidad

Ahora definimos las frecuencias de corte como las frecuencias \( \omega_c \) en las que la potencia \( P_a(\omega) \) en (III) es la mitad de la potencia máxima \( P_{a max} \) en (IV).
Por lo tanto, necesitamos resolver la ecuación
\( P_a (\omega_c ) = \dfrac{1}{2} \left(\dfrac{V_0^2}{2 \; R} \right) \)

\( \dfrac{V_0^2 R}{2 \left({R^2 + \left(\omega_c L - \dfrac{1}{\omega_c C} \right)^2} \right) } = \dfrac{1}{2} \dfrac{V_0^2}{2 \; R} \)
Simplificar a
\( \dfrac{ R}{2 \left({R^2 + \left(\omega_c L - \dfrac{1}{\omega_c C} \right)^2} \right) } = \dfrac{1}{4 R} \)
Multiplicar cruzado, simplificar y reescribir la ecuación anterior como
\( (\omega_c L - \dfrac {1}{\omega_c C } ) = R^2 \)
Resolver extrayendo la raíz cuadrada para obtener dos ecuaciones
\( \omega_c L - \dfrac {1}{\omega_c C} = \pm R \)
Multiplicar todos los términos por \( \omega_c C \) y simplificar
\( \omega_c^2 L C \pm \omega_c R C - 1 = \pm \omega_c R C \)
Reescribir como ecuaciones cuadráticas en forma estándar
\( \omega_c^2 L C \pm \omega_c R C - 1 = 0\)
Resolver la primera ecuación cuadrática \( \quad \omega_c^2 L C + \omega_c R C - 1 = 0\)
para obtener dos soluciones
\( \omega_{c1} = \dfrac {- R C \pm \sqrt{ (R C)^2 + 4 L C }}{ 2 L C } \)

Resolver la segunda ecuación cuadrática \( \quad \omega_c^2 L C - \omega_c R C - 1=0\)
para obtener dos soluciones
\( \omega_{c2} = \dfrac {R C \pm \sqrt{ (R C)^2 + 4 L C}}{ 2 L C } \)
Tenemos un total de 4 soluciones. Tenga en cuenta que la cantidad \( \sqrt{ (R C)^2 + 4 L C } \) es mayor que \( RC \) y, por lo tanto, solo dos soluciones son válidas ya que la frecuencia de corte es una cantidad positiva.
Las frecuencias de corte \( \omega_{c1} \) y \( \omega_{c2} \) son las dos soluciones dadas
\( \omega_{c1} = \dfrac {- R C + \sqrt{ (R C)^2 + 4 L C }}{ 2 L C } \)

\( \omega_{c2} = \dfrac {R C + \sqrt{ (R C)^2 + 4 L C}}{ 2 L C } \)
Ya encontramos la frecuencia resonante \( \omega_r = \dfrac{1}{\sqrt{LC}} \)
Use álgebra simple para reescribir \( \omega_{c1} \) y \( \omega_{c1} \) en términos de \( \omega_r \)
\[ \omega_{c1} = - \dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} \quad \quad (V) \]
\[ \omega_{c2} = \dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} \quad \quad (VI) \]

Nota que
\[ \omega_{c1} \times \omega_{c2} = \omega_r^2 \quad \quad (VII) \]

La anchura de banda del circuito resonante se define por: \( \Delta \omega = \omega_{c2} - \omega_{c1} \)

El factor de calidad \( Q \) se define como
\( Q = \dfrac{\omega_r}{\Delta \omega} \)
Sustituir
\( Q = \dfrac {\omega_r} { \left(\dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} - \left(-\dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} \right) \right)} \)
Simplificar
\[ Q = \omega_r \dfrac{L}{R} \quad \quad (VIII) \]

D - Más Ejemplos con Soluciones Detalladas

Ejemplo 3
Se debe diseñar un circuito resonante serie RLC para que tenga las frecuencias \( f_{c_1} = 650 \) Hertz y \( f_{c_2} = 950 \) Hertz como frecuencias de corte inferior y superior.
a) Calcula la capacitancia del condensador \( C \) y la inductancia del inductor \( L \) si la resistencia del resistor \( R \) es igual a \( 30 \Omega \).
b) ¿Cuál es el factor de calidad del circuito?

Solución al Ejemplo 3
a)
Calcula las frecuencias angulares.
\( \omega_{c_1} = 2 \pi f_{c_1} = 1300 \pi \) rad/s
\( \omega_{c_2} = 2 \pi f_{c_1} = 1900 \pi \) rad/s
Usa la fórmula (VII) desarrollada anteriormente
\( \omega_{c_1} \times \omega_{c_2} = \omega_{r}^2 \) para calcular la frecuencia resonante \( \omega_{r} \) del circuito.
\( \omega_{r} = \sqrt {\omega_{c_1} \times \omega_{c_2}} = \sqrt {1300 \pi \times 1900 \pi } = 100 \sqrt{247} \pi = 4937.400 \) rad/s
\( \omega_{c_2} - \omega_{c_1} = \dfrac{R}{L} \)
Por lo tanto
\( L = \dfrac{R } {\omega_{c_2} - \omega_{c_1}} = \dfrac{30} {1900 \pi - 1300 \pi } = 0.01591 \) H
\( \omega_{r} = \dfrac{1}{\sqrt {L C} } \)
Por lo tanto
\( C = \dfrac{1}{\omega_{r}^2 L} = \dfrac{1}{(100 \sqrt{247} \pi)^2 \times 0.01591} = 2.5783 \times 10^{-6} \) F

b)
El factor de calidad se da por
\( Q = \dfrac{\omega_{r}}{\omega_{c_2} - \omega_{c_1}} = \dfrac{100 \sqrt{247} \pi}{1900 \pi - 1300 \pi } = 2.62\)

Más Referencias y Enlaces

• Calculadora de Circuitos Resonantes Serie RLC
• Circuitos serie RLC
• Calculadora de Impedancia de Circuitos Serie RLC
• Calculadora de Impedancia de Circuitos Paralelos RLC
• Calculadora Gráfica de Corriente en Serie RLC