Cálculos de Corriente y Voltajes en Circuito Serie RLC

Tabla de Contenidos

Aquí se discute cómo se utilizan impedancias complejas para analizar corrientes y voltajes en circuitos serie RLC. Los números complejos simplifican en gran medida los cálculos de impedancias, corrientes y voltajes en circuitos de corriente alterna (AC).
Debido a que el símbolo \(i\) se utiliza para corrientes en circuitos AC, aquí usamos \(j\) como la unidad imaginaria definida por \(j^2 = -1\) o \(j = \sqrt{-1}\).
Se utilizan letras minúsculas para cantidades reales y letras mayúsculas para cantidades complejas en forma polar.

A - Impedancias como Números Complejos y Fasores de un Circuito Serie RLC

Para un circuito alimentado por una fuente de voltaje de frecuencia \(f\), las impedancias de los diferentes componentes RLC se dan por:
Las impedancias en forma compleja \(Z_R\) de una resistencia de resistencia \(R\) se dan por \[ Z_R = R \] Las impedancias en forma compleja \(Z_L\) de una bobina de inductancia \(L\), también llamada reactancia inductiva, se dan por \[ Z_L = j \omega L \] Las impedancias en forma compleja \(Z_C\) de un condensador de capacitancia \(C\), también llamada reactancia capacitiva, se dan por \[ Z_C = - \dfrac{1}{\omega C} j \] donde \(\omega = 2 \pi f\)
Lo más importante a tener en cuenta es que las reactancias inductiva y capacitiva dependen de la frecuencia de la fuente de voltaje.

Sean \(V_i\), \(I\), \(V_R\), \(V_L\) y \(V_C\) la forma compleja de \(v_i\), \(i\), \(v_R\), \(v_L\) y \(v_C\) respectivamente.
Aplicar la Ley de Voltajes de Kirchhoff extendida a impedancias complejas para escribir
\(V_i - V_R - V_L - V_C = 0\)     (1)
Aplicar la Ley de Ohm extendida a impedancias complejas para escribir
\(V_R = Z_R I\)
\(V_L = Z_L I\)
\(V_C = Z_C I\)
Sustituir lo anterior en la ecuación (1) para obtener
\(V_i = Z_R I + Z_L I + Z_C I = 0\)
Resolver lo anterior para \(I\)
\(I = \dfrac{V_i}{Z_R + Z_L + Z_C}\)
Sea \(Z\) la impedancia compleja equivalente del circuito serie RLC definida como
\[ Z = Z_R + Z_L + Z_C = R + j \left(\omega L - \dfrac{1}{\omega C} \right) \]
El módulo de \(Z\): \[ |Z| = \sqrt{R^2 + \left(\omega L - \dfrac{1}{\omega C}\right)^2} \]
El argumento de \(Z\): \[ \theta = \arctan \left( \dfrac {\omega L - \dfrac{1}{\omega C}}{R} \right) \]
Note que tanto el módulo como el argumento de la impedancia \(Z\) dependen de la frecuencia (\( \omega = 2 \pi f \)) de la fuente de voltaje. Esta propiedad es útil en el diseño de filtros y tiene muchas otras aplicaciones en circuitos electrónicos.
Escribir \(Z\) en forma polar
\[ Z = |Z| \; \angle \; \theta \]
Las expresiones para \(Z_R, Z_L, Z_C\) y \(Z\), realizadas anteriormente, pueden interpretarse geométricamente utilizando fasores como se muestra a continuación.


En la parte (a), \(Z_R, Z_L\) y \(Z_C\) se trazan en un sistema de ejes con la parte real a lo largo del eje horizontal y la parte imaginaria a lo largo del eje vertical.
En la parte (b), \(Z = Z_R + Z_L + Z_C\) se traza geométricamente utilizando la adición de vectores (o números complejos).
En la parte (c), un triángulo rectángulo con hipotenusa representando el módulo de \(Z\): usando el teorema de Pitágoras: \( |Z| = \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C}\right)^2} \) exactamente como se obtuvo anteriormente usando números complejos.
Nuevamente, utilizando el triángulo rectángulo, el ángulo: \( \theta = \arctan \left (\dfrac{\omega L - \dfrac{1}{\omega C}}{R} \right) \)

B - Corriente y Voltajes de un circuito serie RLC

Sea \( v_i = V_0 \cos (\omega t) \), \( V_0 \) el pico del voltaje de la fuente
Fórmula de Euler para números complejos
\( e^{j \omega t} = \cos (\omega t) + j \sin (\omega t) \)
Por lo tanto, \( v_i \) también puede expresarse como
\( v_i \) es igual a la parte real de \( e^{j \omega t} \)
Ahora eliminamos la "Parte real de" y realizamos todos los cálculos en números complejos, definiendo \( V_i \) en forma compleja como
\( V_i = V_0 e^{j \omega t} \)
y deducimos \( I \) en forma compleja
\( I = \frac{V_0 e^{j\omega t}}{|Z| \; \angle \; \theta} \)
y \( I \) en forma polar está dada por
\( I = \dfrac{V_0}{|Z|} \; \angle \; \omega t - \theta \)
\( I = I_0 \; \angle \; \omega t - \theta \), donde \( I_0 = \dfrac{V_0}{|Z|} \)
Reescribe las impedancias \( Z_R, Z_L\) y \( Z_C \) en forma polar
\( Z_R = R = R \; \angle \; 0 \)
\( Z_L = j \omega L = \omega L \; \angle \; \pi/2\)
\( Z_C = - \dfrac{1}{\omega C} j = \dfrac{1}{\omega C} \; \angle \; - \pi/2\)
Los voltajes se dan por
\( V_R = Z_R I = (R \; \angle \; 0) (I_0 \; \angle \; {\omega t - \theta}) = R I_0 \angle \; \omega t - \theta \)
\( V_L = Z_L I = (\omega L \; \angle \; \pi/2) (I_0 \; \angle \; {j\omega t - \theta}) = \omega L I_0 \; \angle \; {\omega t - \theta + \pi/2} \)
\( V_C = Z_C I = (\dfrac{1}{\omega C} \; \angle \; - \pi/2) (I_0 \; \angle \; {j\omega t - \theta}) = \dfrac{I_0}{\omega C} \; \angle \; {\omega t - \theta - \pi/2} \)
La corriente \( I \) y los voltajes \( V_R \), \( V_C \) y \( V_C \) se muestran a continuación utilizando fasores.

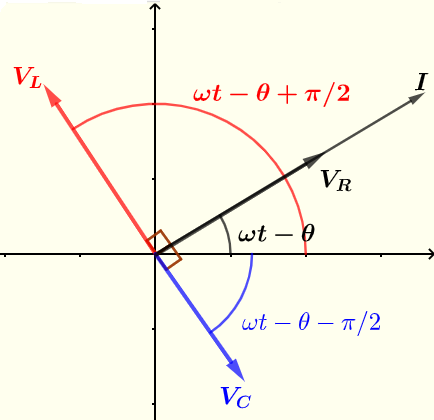
La corriente y los voltajes reales se obtienen a partir de la parte real de la forma compleja (o polar) de la corriente y los voltajes obtenidos anteriormente.
\( i = \dfrac{V_0}{|Z|} \cos( \omega t - \theta) \)

\( v_R = R \dfrac{V_0}{|Z|} \cos(\omega t - \theta) \)

\( v_L = \omega L \dfrac{V_0}{|Z|} \cos(\omega t - \theta + \pi/2) \)

\( v_C = \dfrac{V_0}{\omega C|Z|} \cos(\omega t - \theta - \pi/2) \)

NOTA que la variación temporal \( \omega t \) se puede omitir durante los cálculos y se puede agregar al final si es necesario escribir corrientes y voltajes como una función del tiempo. Los ejemplos a continuación muestran cómo se analizan los circuitos RLC ignorando la dependencia temporal.

C - Ejemplos con Soluciones Detalladas

Ejemplo 1
En un circuito serie RLC, el voltaje de la fuente es \( v_i = 20 \cos (\omega t) \), donde \( \omega = 1000 \; rad/s \), la capacitancia del condensador \( C = 200 \; \mu F \), la inductancia de la bobina \( L = 400 \; mH\) y la resistencia de la resistencia \( R = 400 \; \Omega \).
a) Encuentra las impedancias del condensador, la bobina y la resistencia, y la impedancia \( Z \) equivalente al circuito RLC en forma compleja.
b) Encuentra la corriente y todos los voltajes en forma compleja.
c) Encuentra la corriente y los voltajes reales.

Solución al Ejemplo 1
a)
Las impedancias en forma compleja \( Z_R \) de una resistencia de resistencia \( R \) se dan por
\( Z_R = R = 400 \; \Omega \)
Las impedancias en forma compleja \( Z_L \) de una bobina de inductancia \( L \), también llamada reactancia inductiva, se dan por
\( Z_L = j \omega L = j \cdot 1000 \cdot 400 \cdot 10^{-3} = 400 j \; \Omega \)
Las impedancias en forma compleja \( Z_C \) de un condensador de capacitancia \( C \), también llamada reactancia capacitiva, se dan por
\( Z_C = - \dfrac{1}{\omega C} j = - \dfrac{1}{1000 \cdot 200 \cdot 10^-6} j = - 5 j \; \Omega \)
\( Z = Z_R + Z_L + Z_C = 400 + 400 j - 5 j = 400 + 395 j \)
b)
\( v_i = 20 \cos (\omega t) \), por lo tanto, la forma polar del voltaje de la fuente \( V_i = 20 \; \angle \; 0\)
Hemos visto anteriormente que la corriente en forma polar está dada por
\( I = \dfrac{V_i}{Z_R + Z_L + Z_C} \)
Sustituye las cantidades conocidas
\( I = \dfrac{20 \; \angle \; 0}{400 + 395 j}\)
Reescribe el denominador en forma polar
\( 400 + 395 j = \sqrt {400^2+395^2} \; \angle \; \arctan\left(\dfrac{395}{400}\right) = 562.16 \; \angle \; 44.64^{\circ} \)
Evalúa \( I \)
\( I = \dfrac{20 \; \angle \; 0}{562.16 \; \angle \; 44.64^{\circ}} = \dfrac{20}{562.16} \; \angle \; 0 - 44.64^{\circ} \)
Simplifica
\( I = 0.0356 \; \; \angle \; - 44.64^{\circ} \) A
\( V_R = R I = 400 (0.0356 \; \; \angle \; - 44.64^{\circ}) = 14.24 \; V \; \angle \; - 44.64^{\circ}\) V
\( V_L = Z_L I = 400 j (0.0356 \; \; \angle \; - 44.64^{\circ}) = 14.24 \; V \; \angle \; 45.36^{\circ}\) V
\( V_C = Z_C I = - 5 j (0.0356 \; \; \angle \; - 44.64^{\circ}) = 0.18 \; V \; \angle \; -134.6^{\circ}\) V

Ejemplo 2
En un circuito RLC en serie, el voltaje de la fuente se da por \( v_i = 10 \cos (\omega t) \), la capacitancia del condensador \( C = 200 \; \mu F \), la inductancia de la bobina \( L = 200 \; mH\) y la resistencia del resistor \( R = 500 \; \Omega \).
a) Encuentra la frecuencia angular \( \omega \) para la cual la parte imaginaria de la impedancia \( Z \) es igual a cero.
b) Encuentra la corriente y los voltajes para la frecuencia encontrada en la parte a).

Solución al Ejemplo 2
a)
Para un circuito RLC en serie \( Z = R + j(\omega L - \dfrac{1}{\omega C} ) \)
La parte imaginaria de \( Z \) igual a cero da
\( \omega L - \dfrac{1}{\omega C} = 0 \)
Resuelve para \( \omega \)
\( \omega^2 L C = 1 \)
\( \omega = \dfrac{1}{\sqrt{L C}} \)
Sustituye \( L \) y \( C \) por sus valores numéricos
\( \omega = \dfrac{1}{ \sqrt{ 200\cdot10^{-3} \cdot 200 \cdot 10^{-6}}} = 158.11 \) rad/s
b)
\( I = \dfrac{V_i}{Z} = \dfrac{10 \; \angle \; 0}{R \; \angle \; 0} = \dfrac{10}{500} \; \angle \; 0 = 0.02 \; \angle\; 0 \)
\( V_R = R I = 500 \cdot 0.02 \; \angle \; 0 = 10 \; \angle\; 0 \)
\( V_C = Z_C I = \dfrac{1}{\omega C} \; \angle \; -90^{\circ} \cdot 0.02 \; \angle\; 0 = \dfrac{1}{\omega C} \cdot 0.02 \; \angle \; -90^{\circ} = \dfrac{1}{158.11 \cdot 200 \cdot 10^{-6}} \cdot 0.02 \; \angle \; -90^{\circ} = 0.6324 \; \angle \; -90^{\circ} \)
\( V_L = Z_L I = \omega L \; \angle \; 90^{\circ} \cdot 0.02 \; \angle\; 0 = \omega L \cdot 0.02 \; \angle \; 90^{\circ} = 158.11 \cdot 200 10^{-3} \cdot 0.02 \; \angle \; 90^{\circ} = 0.6324 \; \angle \; 90^{\circ} \)

Ejemplo 3
En un circuito RLC en serie, el voltaje de la fuente se da por \( v_i = V_0 \cos (2 \pi f t) \), donde \( f \) es la frecuencia, la capacitancia del condensador \( C = 47 \; \mu F \), la inductancia de la bobina \( L = 100 \; mH\) y la resistencia del resistor \( R = 200 \; \Omega \).
a) Encuentra la impedancia total \( Z \) equivalente al capacitor, la bobina y la resistencia en serie en función de la frecuencia \( f \) y escríbela en forma polar \( Z = |Z| \; \angle \; \theta \)
b) Encuentra la frecuencia \( f \) tal que \( \theta = -60^{\circ} \).

Solución al Ejemplo 3
a)
Para un circuito RLC en serie \( Z = R + j(\omega L - \dfrac{1}{\omega C}) \)
Sustituye las cantidades conocidas por sus valores numéricos
\( Z = R + j(\omega L - \dfrac{1}{\omega C}) = 200 + j( \omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}})\)
\( Z = \sqrt {200^2 + ( \omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}})^2} \; \angle \; \arctan \left(\dfrac{\omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}}}{200}\right) \)
b)
\( \arctan \left(\dfrac{\omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}}}{200}\right) = -60^{\circ} \)
\( \dfrac{\omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}}}{200} = \tan (-60^{\circ}) = -1.73205 \)
Multiplica todos los términos de la ecuación por \( 200 \) para eliminar el denominador
\( \omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}} = -346.41 \)
Multiplica todos los términos de la ecuación por \( \omega \cdot 47 \cdot 10^{-6} \) para eliminar el denominador
\( 47 \cdot 10^{-7} \omega^2 - 1 = -0.01628127 \omega \)
Resuelve la ecuación cuadrática anterior para \( \omega \) y selecciona la solución positiva.
\( \omega = 53.23 \) rad/s
\( \omega = 2 \pi f = 60.3682 \)
\( f = \dfrac{60.3682}{2 \pi} = 9.60789 \) Hz

Ejemplo 4
En un circuito RLC en serie, el voltaje de la fuente se da por \( v_i = V_0 \cos (2 \pi f t) \), la capacitancia del condensador \( C = 470 \mu \)F, la inductancia de la bobina \( L = 50 \)mH y la resistencia del resistor es \( R \).
a) Encuentra la impedancia total \( Z \) equivalente al capacitor, la bobina y la resistencia en serie en función de la frecuencia \( f \) y escríbela en forma polar \( Z = |Z| \; \angle \; \theta \)
b) Encuentra la resistencia \( R \) y la frecuencia \( f \) tal que \( \theta = 40^{\circ} \) y \( |Z| = 100 \).

Solución al Ejemplo 4
a)
Para un circuito RLC en serie \( Z = R + j(\omega L - \dfrac{1}{\omega C}) \)
Escribe \( Z \) en forma polar
\( Z = \sqrt{R^2 + (\omega L - \dfrac{1}{\omega C})^2} \; \angle \; \arctan \left( \dfrac{\omega L - \dfrac{1}{\omega C}}{R} \right) \)
b)
\( \theta = \arctan \left( \dfrac{\omega L - \dfrac{1}{\omega C}}{R} \right) = 40^{\circ} \)
\( \dfrac{\omega L - \dfrac{1}{\omega C}}{R} = \tan 40^{\circ} = 0.83909\)
\( \omega L - \dfrac{1}{\omega C} = 0.83909 R \)
Sustituye lo anterior en \( |Z| \)
\( \sqrt{R^2 + (0.83909 R)^2} = 100 \)
Resuelve para \( R \)
\( R = 76.6048 \; \Omega \)
\( \omega L - \dfrac{1}{\omega C} = 0.83909 R = 64.27832 \)
Resuelve para \( \omega \)
\( \omega = 1317.8557 \) rad/s
\( f = \dfrac{1317.8557}{2\pi} = 209.74324 \) Hz

Más Referencias y Enlaces