Uso de Números Complejos en Circuitos de CA

Tabla de Contenidos

Aquí se discute cómo los números complejos pueden ser utilizados para analizar y calcular corrientes y voltajes en circuitos de corriente alterna (CA), así como cómo la resistencia, la impedancia de un condensador y la impedancia de una bobina están representadas por números complejos. También se muestra cómo el uso de impedancias complejas permite utilizar una ley similar a la ley de Ohm para modelar matemáticamente los circuitos de CA.
Dos razones principales que hacen que el uso de números complejos sea adecuado para modelar circuitos de CA, y muchos otros fenómenos de ondas sinusoidales en diversas ramas de la ingeniería, son:
1) las señales de CA (y muchos otros fenómenos de ondas sinusoidales) se caracterizan por una magnitud y una fase que son, respectivamente, muy similares al módulo y argumento de los números complejos.
2) las operaciones básicas como la suma, resta, multiplicación y división de números complejos son más fáciles de llevar a cabo y programar en una computadora.
Nota
1) Debido a que el símbolo \( i \) se usa para corrientes en circuitos de CA, aquí usamos \( j \) como la unidad imaginaria definida por \( j^2 = -1 \) o \( j = \sqrt{-1} \)
2) El símbolo \( \Re e\) representa la parte real de un número complejo.

A - Parte Real de Números Complejos

Un número complejo en forma estándar \( Z = a + j b \) puede escribirse en forma exponencial de la siguiente manera
\( \displaystyle Z = r e^{j \theta} \)      con \( j^2 = -1 \)
y en forma polar de la siguiente manera
\( Z = r \angle \theta \)
donde \( r = \sqrt{a^2 +b^2} \) es el módulo de \( Z \) y \( \tan \theta = \dfrac{b}{a} \) su argumento.
Tomando la parte real, escrita como \( \Re e \) , de cada lado de un número complejo en forma exponencial
\( \Re e (r e^{j \theta}) = \Re e (r ( \cos \theta + j \sin \theta )) = \Re e (r \cos \theta + j r \sin \theta ) = r \cos \theta \)
En lo que sigue, \( \Re e \) significa la parte real de un número complejo dado.

B - Derivada de Funciones Complejas con una Variable

Sea \( f(t) \) una función compleja con una variable \( t \) escrita de la forma
\( f(t) = a(t) + j b(t) \)
donde \( a(t) \) es la parte real de \( f(t) \), \( b(t) \) es la parte imaginaria de \( f(t) \) y \( j = \sqrt {-1}\) es la unidad imaginaria.
Sea \( f'(t) \) la primera derivada de \( f(t) \) con respecto a \( t \) definida por
\( f'(t) = \lim_{h\to 0} \dfrac{f(t+h) - f(t) }{h} \)
Sustituimos \( f(t+h) \) por \( a(t+h) + j b(t+h) \) en la fórmula anterior.
\( f'(t) = \lim_{h\to 0} \dfrac{ a(t+h) + j b(t+h) - (a(t) + jb(t))}{h} \)
Separamos los términos de la siguiente manera
\( f'(t) = \lim_{h\to 0} \dfrac{ a(t+h) - a(t)}{h} + j \lim_{h\to 0} \dfrac{ j b(t+h) - jb(t))}{h} \)
\( f'(t) = a'(t) + j b'(t) \)
Ahora es fácil mostrar que la parte real de la derivada de \( f(t) \) es igual a la derivada de la parte real de \( f(t) \), lo cual puede escribirse como
\( \Re e(f'(t)) = a'(t) = (\Re e(f(t))' \)
o
\( \Re e \left ( \dfrac{df(t)}{dt} \right) = \dfrac {d a(t)}{dt} = \dfrac {d \left (\Re e(f(t)) \right)}{dt} \)

C - Integral de Funciones Complejas con una Variable

Sea \( f(t) \) una función compleja con una variable \( t \) escrita de la forma
\( f(t) = a(t) + j b(t) \)
donde \( a(t) \) es la parte real de \( f(t) \), \( b(t) \) es la parte imaginaria de \( f(t) \) y \( j = \sqrt {-1}\) es la unidad imaginaria.
Sea \( F(t) \) definida por la integral indefinida
\( \displaystyle F(t) = \int f(t) dt = \int (a(t) + j b(t)) dt = \int a(t) dt + j \int b(t) dt \)
Ahora es fácil mostrar que la parte real de la integral indefinida de \( f(t) \) es igual a la integral indefinida de la parte real de \( f(t) \), lo cual puede escribirse como
\( \displaystyle \Re e \left( \int f(t) dt \right) = \int a(t) dt = \int \left( \Re e f(t) \right) dt \)

Ahora utilizamos los conceptos anteriores para analizar circuitos de CA simples utilizando números complejos.

D - Fuente de Voltaje de CA y Números Complejos

En lo que sigue, \( v(t) \) es una fuente de voltaje de CA, que varía con el tiempo \( t \), dada por
\( v(t) = V_0 \cos(\omega t) \)
donde \( V_0 \) es un número real igual al voltaje pico y \( \omega = 2 \pi f \) es también un número real con \( f \) como la frecuencia de la fuente de voltaje.
Utilizando números complejos, \( v(t) \) también puede escribirse como
\( v(t) = V_0 \cos(\omega t) = \Re e ( V_0 \cos(\omega t) + j V_0 \sin(\omega t) ) = \Re e (V_0 e^{j\omega t} ) \)

E - Resistor en Circuito de CA

Consideremos un circuito de CA simple con un resistor como se muestra a continuación. Sea \( v(t) \) una fuente de voltaje de CA dada por
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
donde \( V_0 \) y \( \omega \) son cantidades reales.


La relación entre la corriente \( i \) a través y el voltaje \( v(t)_R \) a través del resistor \( R \) viene dada por
\( v(t)_R = R i \)
Utilizando la única trayectoria mostrada arriba, tenemos
\( v(t) = v(t)_R \)
\( v(t) \) es dado por \( v(t) = V_0 \cos(\omega t) \)
entonces
\( v(t)_R = V_0 cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
combinando lo anterior, escribimos
\( R i = \Re e (V_0 e^{j\omega t} ) \)       (I)
Sea \( V_R = V_0 e^{j\omega t} \) y reescribimos (I) anteriormente como
\( R i = \Re e V_R \)
ya que \( R \) es una cantidad real, lo anterior puede escribirse como
\( i = \Re e \left( \dfrac{V_R }{R} \right) \)
Sea \( Z_R \) definido como la impedancia de un resistor tal que
\( Z_R = R \)
Dado que \( R \) es real, la impedancia \( Z_R \) de un resistor es un número real.
La corriente \( i \) puede entonces escribirse como
\( i = \Re e \left( \dfrac{ V_R } {Z_R} \right) \)
Sea
\( I = \dfrac{ V_R } {Z_R} \)
Lo anterior proporciona una relación similar a la ley de Ohm en circuitos de corriente continua (CC). La relación anterior entre las cantidades complejas \( I \), \( V_R \) y \( R \) facilita mucho los cálculos.
Esto simplifica los cálculos en el sentido de que realizamos cálculos utilizando impedancias complejas, voltaje y corriente y luego tomamos la parte real como respuesta final.

F - Condensador en un Circuito de CA

Consideremos un circuito de CA simple con un condensador como se muestra a continuación. Sea \( v(t) \) una fuente de voltaje de CA dada por
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)

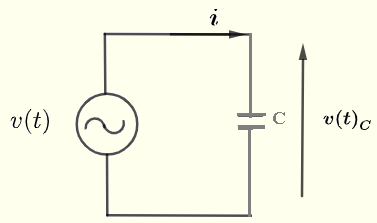
La relación entre la corriente \( i \) a través y el voltaje \( v(t)_C \) a través del condensador \( C \) viene dada por
\( \displaystyle v(t)_C = \dfrac{1}{C} \int i dt \)
Utilizando el único bucle mostrado arriba, tenemos
\( v(t) = v(t)_C \)
Dado
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
combinamos todo lo anterior para escribir
\( \displaystyle \Re e (V_0 e^{j\omega t} ) = \dfrac{1}{C} \int i dt \)
Tomemos la derivada de ambos lados
\( \displaystyle \dfrac{d}{dt} (\Re e (V_0 e^{j\omega t}) ) = \dfrac{d}{dt} \left(\dfrac{1}{C} \int i dt \right) \)
Usando el resultado discutido anteriormente en la parte B, reescribimos lo anterior como
\( \displaystyle \Re e \dfrac{d}{dt} \left( V_0 e^{j\omega t} \right) = \dfrac{d}{dt} \left(\dfrac{1}{C} \int i dt \right) \)
Simplificamos
\( \Re e \left( j \omega V_0 e^{j\omega t} \right) = \dfrac{1}{C} i \)
Dado que la capacitancia \( C \) es una cantidad real, podemos escribir
\( i = \Re e \left( j \omega C \; V_0 e^{j\omega t} \right) \)
Sea \( V_C = V_0 e^{j\omega t} \) y definamos \( Z_C \) como la impedancia compleja de un condensador tal que
\( Z_C = \dfrac{1}{j \omega C} = - \dfrac {j} { \omega C} \)
Dado que \( C \) es real, la impedancia \( Z_C \) de un condensador es un número imaginario puro.
La corriente \( i \) puede entonces escribirse como
\( i = \Re e \left( \dfrac{ V_C } {Z_C} \right) \)
Sea
\( I = \dfrac{ V_C } {Z_C} \)
Lo anterior es similar a la ley de Ohm en circuitos de corriente continua (CC). La relación anterior entre las cantidades complejas \( I \), \( V_C \) y \( Z_C \) facilita mucho los cálculos.
Esto simplifica los cálculos en el sentido de que realizamos cálculos utilizando impedancias complejas, voltaje y corriente y luego tomamos la parte real como respuesta final.

G - Inductor en un Circuito de CA

Consideremos un circuito de CA simple con un inductor como se muestra a continuación. Sea \( v(t) \) una fuente de voltaje de CA dada por
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)

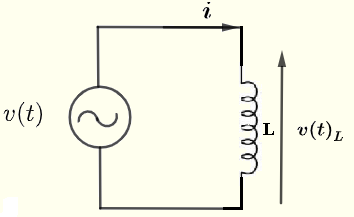
La relación entre la corriente \( i \) a través y el voltaje \( v(t)_L \) a través del inductor con inductancia \( L \) viene dada por
\( v(t)_L = L \dfrac {d i}{ dt} \)
Utilizando el único bucle mostrado arriba, tenemos
\( v(t) = v(t)_L \)
Dado
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
combinamos todo lo anterior para escribir
\( \Re e (V_0 e^{j\omega t} ) = L \dfrac {d i}{ dt} \)
Tomemos la integral indefinida de ambos lados
\( \displaystyle \int \Re e (V_0 e^{j\omega t}) dt = \int L \dfrac {d i}{ dt} dt \)
Usando el resultado ya discutido en la parte C anterior, reescribimos lo anterior como
\( \displaystyle \Re e \int V_0 e^{j\omega t} dt = \int L \dfrac {d i}{ dt} dt \)
Calculamos las integrales en ambos lados
\( \Re e \left( \dfrac{1}{j\omega} V_0 e^{j\omega t} \right) = L i \)
Dado que la inductancia \( L \) es una cantidad real, podemos escribir
\( i = \Re e \left( \dfrac{1}{j \omega L} \; V_0 e^{j\omega t} \right) \)
Sea \( V_L = V_0 e^{j\omega t} \) y \( Z_L \) esté definido como la impedancia de un inductor tal que
\( Z_L = j \omega L \)
Dado que \( L \) es real, la impedancia \( Z_L \) de un inductor es un número imaginario puro.
La corriente \( i \) puede entonces escribirse como
\( i = \Re e \left( \dfrac{ V_L } {Z_L} \right) \)
Sea
\( I = \dfrac{ V_L } {Z_L} \)
Lo anterior proporciona una relación similar a la ley de Ohm entre cantidades complejas \( I \), \( V_L \) y \( Z_L \).
Esto simplifica los cálculos en el sentido de que realizamos cálculos utilizando impedancias complejas, voltaje y corriente y luego tomamos la parte real como respuesta final.

H - Conclusión: Ley de Ohm con Impedancias Complejas

Hemos visto anteriormente que las impedancias de resistencias, condensadores e inductores se pueden definir como cantidades complejas que pueden ser puramente reales o puramente imaginarias, dadas por:
1) Para una resistencia \( R \); la impedancia se da por \[ Z_R = R \] y la relación entre la corriente \( I \) (en forma compleja) a través y el voltaje \( V_R \) (en forma compleja) a través de la resistencia \( R \) es la ley de Ohm en CA y se expresa como: \[ I = \dfrac{V_R}{Z_R} \] 2) Para un condensador \( C \); la impedancia se da por \[ Z_C = -\dfrac{j}{\omega C} \] y la relación entre la corriente \( I \) (en forma compleja) a través y el voltaje \( V_C \) (en forma compleja) a través del condensador \( C \) es la ley de Ohm en CA y se expresa como: \[ I = \dfrac{V_C}{Z_C} \] 3) Para una bobina \( L \); la impedancia se da por \[ Z_L = j \omega L \] y la relación entre la corriente \( I \) (en forma compleja) a través y el voltaje \( V_L \) (en forma compleja) a través de la bobina \( L \) es la ley de Ohm en CA y se expresa como: \[ I = \dfrac{V_C}{Z_L} \] Concluimos que la Ley de Ohm es válida en circuitos de CA cuando se utilizan números complejos para modelar impedancias de resistencias, condensadores e inductores.
También se puede demostrar que las leyes de Kirchhoff también son válidas en circuitos de CA cuando se utilizan números complejos para modelar impedancias de resistencias, condensadores e inductores.
Las impedancias equivalentes a impedancias en serie y paralelo se pueden calcular utilizando reglas similares para resistencias en serie y paralelo.

E - Ejemplos con Soluciones

Ejemplo 1
Encuentra la corriente \( i \), el voltaje \( v(t)_R \) a través de la resistencia \( R \) y el voltaje \( v(t)_L \) a través de la bobina \( L \) en términos de \( V_0 \), \( R \), \( L \) y \( \omega \) dado
fuente de voltaje: \( v(t) = V_0 \cos(\omega t) \), \( \omega = 2 \pi f \) y \( f \) es la frecuencia.

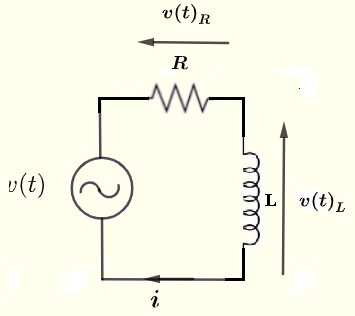
Solución al Ejemplo 1
Sea \( V \) la forma compleja del voltaje de la fuente \( v(t) \).
Sea \( V_R \) la forma compleja del voltaje \( v(t)_R\) a través de la resistencia R.
Sea \( V_L \) la forma compleja del voltaje \( v(t)_L\) a través de la bobina L
Sea \( I \) la forma compleja de la corriente \( i \) a través de la resistencia y el condensador en el circuito dado.
Sea la impedancia compleja de una resistencia \( Z_R = R \) y la de la bobina \( Z_L = j \omega L \) (ver parte H arriba).
Vuelva a dibujar el circuito con las cantidades complejas definidas anteriormente y puede aplicar las leyes de Ohm y Kirchhoff.

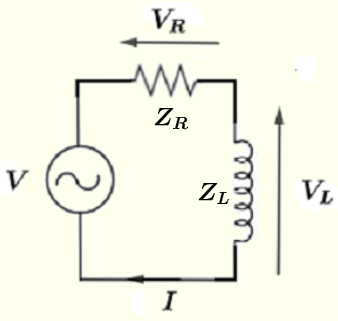
Usando la ley de Kirchhoff en la bucle que forma el circuito, tenemos
\( V = V_R + V_L \)         (I)
Usando la ley de Ohm para reescribir \( V_R \) y \( V_L \) como
\( V_R = Z_R I \)
\( V_L = Z_L I \)
Sustituir en la ecuación (I)
\( V = Z_R I + Z_L I = R I + j \omega L I = I(R + j \omega L ) \)
Resolver lo anterior para \( I \)
\( I = \dfrac{V}{R+j \omega L} \)         (II)
El denominador \( R+j \omega L \) es un número complejo que se puede escribir en forma compleja como
\( R+j \omega L = r e^{j\theta} \)
donde
\( r = |Z| = \sqrt {R^2 + (L\omega)^2} \) es el módulo
\( \theta = \arctan \left(\dfrac{\omega L}{R} \right) \) es el argumento como se muestra en el plano complejo a continuación.

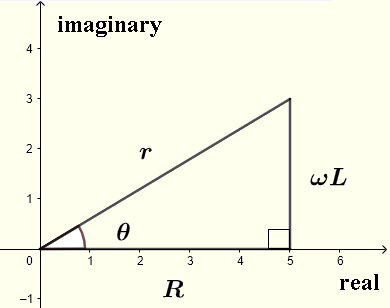
Sea \( V = V_0 e^{j\omega t} \)
Sustituir \( V \) y \( R+j \omega L \) por sus formas complejas en (II) y escribir
\( I = \dfrac{V_0 e^{j\omega t}}{r e^{j\theta}} \)
Usar reglas exponenciales para simplificar lo anterior
\( I = \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
Usar la ley de Ohm para escribir
\( V_R = R I = \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)

\( V_L = Z_L I = \dfrac{j V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
Escribir \( j \) en forma exponencial \( j = e^{j \pi/2} \) en \( V_L \)
\( V_L = \dfrac{ e^{j \pi/2} V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
Usar la regla exponencial para reescribir lo anterior como
\( V_L = \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t + \pi/2 -\theta)} \)
Ahora usamos las cantidades complejas calculadas anteriormente para calcular \( i \), \( v(t)_R \) y \( v(t)_L \) tomando las partes reales de la siguiente manera:
\( i = \Re e I = \Re e \left( \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \right) \)
lo cual da
\[ i = \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t-\theta) \] \( v(t)_R = \Re e V_R = \Re e \left( \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \right) \) \[ v(t)_R = \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t-\theta) \] \( v(t)_L = \Re e V_L = \Re e \left( \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t + \pi/2 -\theta)} \right) \) \[ v(t)_L = \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t + \pi/2 -\theta) \]

Más Referencias y Enlaces