The definition of functions with many variables and the concept of the domain of these functions are presented with examples.
Problems and their solutions are also included.
Skills in solving systems of inequalities with two variables are needed in order to find the domain of functions with two variables.
Let us consider some very well known formulas.
a) The perimeter \( P \) of a square of side \( x \) is given by \( P = 4 x\).
b) The area \( A \) of a rectangle of length \( L \) and width \( W \) is given by \( A = L W \)
c) The force F ,due to Newton's law of universal gravitation, between two objects of masses \( m_1 \) and \( m_2 \) separated by a distance \( d \) is given by \( F = G \dfrac{m_1 m_2}{d^2} \)
where \( G \) is a constant.
It can be said that:
the perimeter \( P \) in part a) above is a function of one variable \( x \)
the area \( A \) in part b) above is a function of two variables \( L \) and \( W \)
the force \( F \) in part c) is a function of three variables variable \( m_1 \), \( m_2 \) and \( d \) (Note that G is a constant).
A function \( f \) of \( n \) variables \( x_1, x_2, ...., x_n \), is a rule that assigns a unique real number \( f (x_1, x_2, ...., x_n) \) to each n-tuples of real numbers \( x_1, x_2, ...., x_n \).
The set \( D \) of all n-tuples of real numbers \( x_1, x_2, ...., x_n \) for which the function \( f \) is uniquely real valued is called the domain of function \( f \).
If we let \( u = f (x_1, x_2, ...., x_n) \), the set of all the values of \( u \) corresponding to all the n-tuples \( x_1, x_2, ...., x_n \) in \( D \) is called the range of \( f \) [1] , [2] , [3] .
Example 1 Function of two Variables
Let function \( f \) defined by
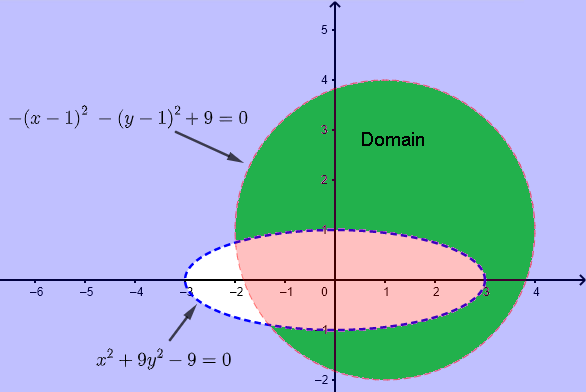
\[ f(x,y) = \sqrt{x^2+y^2} + \ln(x-y) \]
a) Evaluate: \( f(4,3) \) , \( f(e^2,0) \)
b) Find and sketch the domain of \( f \)
Solution to Example 1
a)
To evaluate\( f(4,3) \), we need to substitute \( x \) by \( 4 \) and \( y \) by \( 3 \)
Hence
\( f(4,3) = \sqrt{4^2+3^2} + \ln(4-3) \)
Simplify
\( \quad = \sqrt{25} + \ln(1) = 5 + 0 = 5 \)
To evaluate\( f(e^2,0) \), we need to substitute \( x \) by \( e^2 \) and \( y \) by \( 0 \)
Hence
\( f(e^2,0) = \sqrt{e^2 + 0^2} + \ln(e^2 - 0) \)
Simplify
\( \quad = e + 2 \)
b)
The domain of \( f(x,y) \) is found by setting the conditions:
1) \( \quad x^2+y^2 \ge 0 \), a quantity under the square root must be non negative
2) \( \quad x - y \gt 0 \), the argument of a logarithm must be positive.
Condition 1) above is always satisfied.
The inequality in condition 2) may be solved graphically to obtain the solution shown by the graph below.

Example 2 Function of three Variables
Let function \( g \) defined by
\[ g(x,y,z) = \sqrt{ x^2 + y^2 + z^2 - 9} \]
a) Evaluate: \( g(3,-1,1) \) , \( g(3/2,1/4,7/2) \)
b) Find and describe the domain of \( g \)
Solution to Example 2
a)
To evaluate \( g(3,-1,1) \) , we need to substitute \( x \) by \( 3 \), \( y \) by \( -1 \) and \( z \) by \( 1 \)
Hence
\( g(3,-1,1) = \sqrt{ 3^2 + (-1)^2 + 1^2 - 9} \)
Simplify
\( \quad = \sqrt{2} \)
To evaluate \( g(3/2,1/4,7/2) \), we need to substitute \( x \) by \( 3/2 \), \( y \) by \( 1/4 \) and \( z \) by \( 7/2 \)
Hence
\( g(3/2,1/4,2) = \sqrt{ (3/2)^2 + (1/4)^2 + (7/2)^2 - 9} \)
Simplify
\( \quad = \dfrac{\sqrt{89}}{4} \)
b)
The domain of \( g(x,y,z) \) is found by setting the conditions:
\( x^2 + y^2 + z^2 - 9 \ge 0 \) , a quantity under the square root must be non negative
Consider \( x^2 + y^2 + z^2 - 9 = 0 \) which may be written as \( x^2 + y^2 + z^2 = 3^2 \).
Hence the graph of the equation \( x^2 + y^2 + z^2 - 9 = 0 \) is a sphere of radius \( 3 \) centered at the origin \( (0,0,0) \) as shown below.
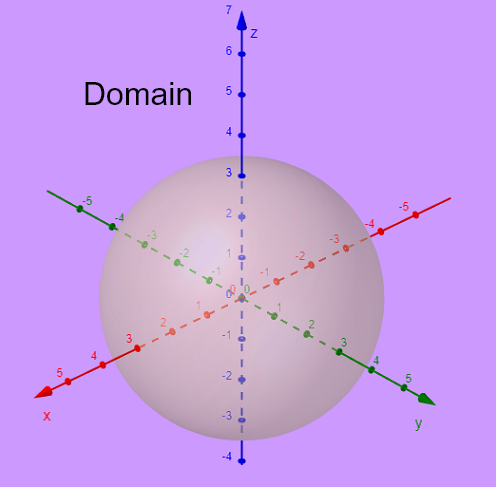
Example 3 Function of two Variables
Let function \( h \) defined by
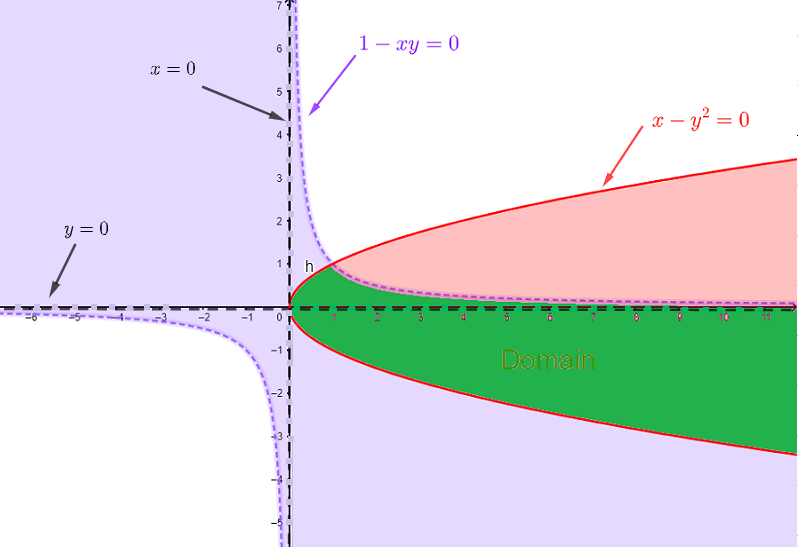
\[ h(x,y) = \dfrac{1}{\ln (1 - x y) } - \sqrt{x - y^2}\]
a) Find and describe the domain of \( h \)
b) Give examples of 3 ordered pairs \( (x,y) \) that are in the domain of \( h \) and evaluate the function at these points.
c) Give examples of 3 ordered pairs \( (x,y) \) that are NOT in the domain.
Solution to Example 3
a)
The domain of \( h(x,y) \) is found by setting the conditions:
1) \( \quad 1 - x y \gt 0 \) , the argument of a logarithm must be positive
2) \( \quad x - y^2 \ge 0 \) , the argument of the square root must be non negative.
3) \( \quad \ln (1 - x y) \ne 0 \) or \( 1 - xy \ne 1 \) which is equivalent to \( xy \ne 0 \), the denominator \( \ln (1 - x y) \) must NOT be equal to zero.
Condition 1) is solved by graphing \( 1 - x y = 0 \) which is equivalent to \( y = \dfrac{1}{x} \) and selecting the solution set as the set of points satisfying the inequality \( \quad 1 - x y \gt 0 \). (light purple color)
Condition 2) is solved by graphing \( x - y^2 = 0 \) which is equivalent to \( x = y^2 \), a horizontal parabola, and selecting the solution set as the set of points satisfying the inequality \( \quad x - y^2 \ge 0 \). (red color)
Condition 3) is satisfied by any points that is NOT on any of the axes. (broken lines on axes)
The domain is the intersection of all the three sets found for conditions 1), 2) and 3) and is shown below in green excluding any points on the \( x \) or \( y \) axes.
Part A
Given the functions:
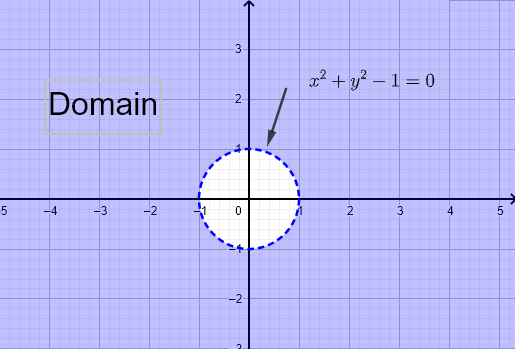
\( f (x,y) = \dfrac{1}{\sqrt{x^2 - y}} \) and \( g (x,y) = \ln (x^2 + y^2 - 1) \)
a) Find the domain of each function
b) Evaluate
1) \( f (1,0) \) , 2) \( g (1,-1) \) , 3) \( \dfrac{f(3,4)}{g(2,0)} \)
Part B
In an electrical circuit, the resistance \( R \) of three resistors in parallel and of resistances \( r_1 , r_2 , r_3 \) are related by
\( \dfrac{1}{R} = \dfrac{1}{r_1} + \dfrac{1}{r_2} + \dfrac{1}{r_3} \)
a) Express \( R \) as a function of the variables \( r_1 , r_2 , r_3 \).
b) Calculate \( R \) for \( r_1 = 100 \) , \( r_2 = 50 \) and \( r_3 = 20 \).
Part C
Find the domain of the functions
a) \( f(x,y) = \sqrt{x^2+y-2x} \)
b) \( h(x,y) = \dfrac{\ln(x^2+9 y^2-9)}{\sqrt{7-x^2-y^2+2 x + 2 y}} \)
Part A
\( f (x,y) = \dfrac{1}{\sqrt{x^2 - y}} \) and \( g (x,y) = \ln (x^2 + y^2 - 1) \)
a)
Domain of \( f \) is found by solving: \( x^2 - y \gt 0 \); the denominator must not be equal to zero and the the argument of the square root must be non negative.
Graph \( y = x^2 \) and select the area satisfying the inequality \( x^2 - y \gt 0 \). The graphical solution is shown below. The domain is the set of all points \( (x,y) \) outside the parabola \( y = x^2 \).

Part B
a)
Given \( \dfrac{1}{R} = \dfrac{1}{r_1} + \dfrac{1}{r_2} + \dfrac{1}{r_3} \),
Multiply all terms of the equaltion by the product \( r_1 r_2 r_3 \)
\( \dfrac{r_1 r_2 r_3}{R} = \dfrac{r_1 r_2 r_3}{r_1} + \dfrac{r_1 r_2 r_3}{r_2} + \dfrac{r_1 r_2 r_3}{r_3} \)
Simplify
\( \dfrac{r_1 r_2 r_3}{R} = r_2 r_3 + r_1 r_3 + r_1 r_2 \)
Solve for \( R \)
\( R(r_1,r_2,r_3) = \dfrac{r_1 r_2 r_3}{r_2 r_3 + r_1 r_3 + r_1 r_2} \)
b)
\( R(100,50,20) = \dfrac{100 \times 50 \times 20}{50 \times 20 + 100 \times 20 + 100 \times 50} = 12.5\)
Part C
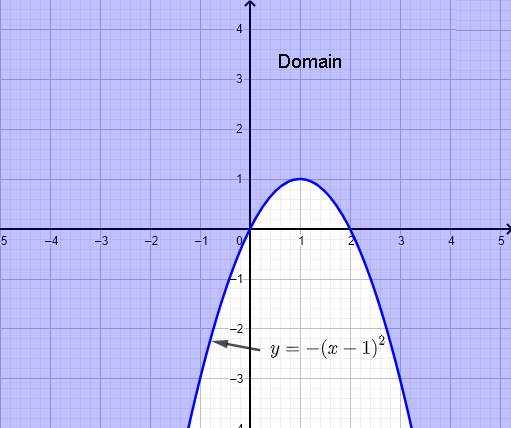
a) \( f(x,y) = \sqrt{x^2+y-2x} \)
\( f(x,y) \) takes real values if the argument of the square root is non negative, hence the condition
\( x^2+y-2x \ge 0 \)
Complete the square and rewrite as
\( (x-1)^2 - 1 + y \ge 0 \)
\( y \ge - (x-1)^2 + 1 \)
Graph the parabola \( y = - (x-1)^2 + 1 \) and identify the domain of function \( f \).
The domain is the set of points \( (x,y) \) on or outside the parabola \( y = - (x-1)^2 + 1 \) as shown in the graph below (purple).