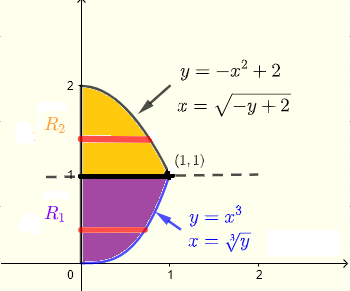Table of Contents
Double Integrals Over General Regions
Examples to calculate and evaluate double integrals over general regions are presented along with their detailed solutions.
Important Notes
1) Making graphs and diagrams for general non rectangular regions as a first step makes it easy to calculate double integrals with general regions.
2) In general four steps are needed in order to calculate double integral over general regions of integration:
STEP 1: Make a graph and/or diagram of the region of integration
STEP 2: Decide on how to describe the general region using either vertical or horizontal strips and therefore the order of integration
STEP 3: Describe the general region of integration using inequalities
STEP 4: Calculate the integral
3) In what follows, we describe a given region \( R \) of integration as either an infinite set of vertical strips which allows the integral to be expressed as \[ \displaystyle \iint_R f(x,y) \;dy \;dx \] or horizontal strips which allows the integral to be expressed as \[ \displaystyle \iint_R f(x,y) \;dx \;dy \]
Calculations of Double Integrals Over General Regions
The objectives of examples 1 and 2 is to use graphs and diagrams to determine the limits of integration for general regions and calculate the double integral.
Example 1
Question: Calculate the double integral \( \displaystyle V = \iint_R (x^2+y) \;dy \;dx \) where the region \( R \) is a triangle on the plane \( xy\)-plane bounded by the \(x\)-axis, the \(y\)-axis and the line \( y = - x + 2 \).
Solution to Example 1
Four major steps to calculate double integrals with general regions of integration.
STEP 1 Make a graph and/or diagram that represents the general region
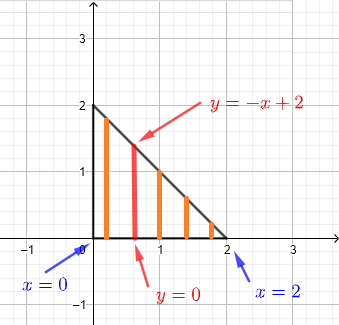
We first start by drawing a graph or/and diagram of the region \( R \) of integration. In this example it is a triangle with sides on the \(x\) and the \(y\)-axes and the third side is described by the equation of the line \( y = - x + 2 \).
This triangle may also be defined by three vertices: the origin and the points of intersection of the line \( y = - x + 2 \) and the
\(x\) and the \(y\)-axes given by \( (2,0) \) and \( (0,2) \) respectively as shown in the graph below.

There are two ways to calculate the given integral over the given region.
STEP 2 Decide on how to describe the general region using strips
1) We use vertical strips to describe the region \( R \) as shown in the graph below.
We assume that the region R may be considered as an infinite set of vertical strips as shown in the diagram below.
Any given vertical strip, at a given \( x \), starts at \( y = 0 \) and ends at \( y = - x + 2 \). Since we have to include all strips that describe region \( R \), \( x \) has to take values from \( x = 0 \) to \( x = 2 \). Hence the region \( R \) of integration may be defined by:
STEP 3 Describe the general region of integration using inequalities
\( R \) : \( 0 \le x \le \ 2 \) , \( 0 \le y \le - x + 2 \)
STEP 4 Calculate the integral
The integral may be written as
\( \displaystyle V = \int_0^2 \int_0^{-x+2} (x^2+y) \;dy \;dx \)
\( = \displaystyle \int_0^2 ( -x^3 +\dfrac{5}{2} x^2 - 2x + 2) \;dx = 8/3\)
We now answer the same question but using horizontal strips.
STEP 1 is the same as above
STEP 2 Decide on how to describe the general region using strips
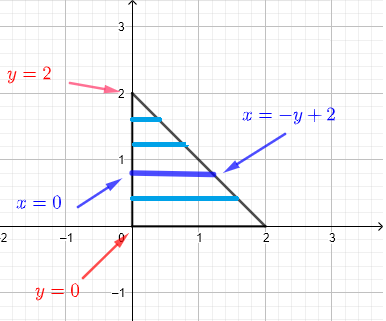
2) We use horizontal strips to describe the region \( R \) as shown in the graph below.
We assume that the region R may be considered as an infinite set of horizontal strips as shown in the diagram below.
Any given vertical strip, at a given \( y \), starts at \( x = 0 \) and ends at \( x = - y + 2 \). Since we have to include all strips in order that describe region \( R \), \( y \) has to take values from \( y = 0 \) to \( y = 2 \). Hence the region \( R \) of integration may be defined by:
STEP 3 Describe the general region of integration using inequalities
\( R \) : \( 0 \le x \le - y + 2 \) , \( 0 \le y \le 2 \)
STEP 4 Calculate the integral
Hence the integral may be written as
\( \displaystyle V = \int_0^2 \int_0^{-y+2} (x^2+y) \;dx \;dy \)
\( = \displaystyle \int_0^2 (-\dfrac{1}{3} y^3 + y^2 - 2 y + \dfrac{8}{3} ) \;dy = 8/3 \)
Notes In both cases, the integral whose limits includes variables is the inner integral
Example 2
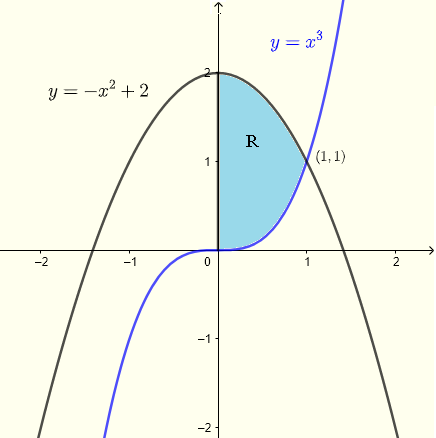
Question: Calculate the double integral \( \displaystyle V = \iint_R (x+y) \;dy \;dx \) where the region \( R \) is on the plane \( xy\)-plane bounded by the \(y\)-axis, the curves of equations \( y = x^3 \) and \( y = - x^2 + 2 \).
Solution to Example 2
We start by analyzing region \( R \) as shown in the graph below. The two curves intersects at a point whose \( x \) coordinate is given by the solution of the system of equations
\( y = x^3 \)
\(y = - x^2 + 2 \)
One way to solve the above system is to subtract the two equations and simplify to eliminate \( y \) and end up with an equation in \(x \) only to obtain the equation
\( 0 = x^3 + x^2 - 2 \)
With the help of the graph, it is easy to see that \( x = 1 \) is a solution to the above system of equation which you can check analytically.
The \(y\)-coordinate of the point of intersection of the two curves is found by substituting \( x \) by the solution already found \( 1 \) in one of the equations of the curves to find \( y = (1)^3 = 1 \).
Hence the point of intersection is given by \( (1,1) \)
1) Using vertical strips
A given vertical strip starts on the curve \( y = x^3 \) and ends on the curve \( x = - x^2 + 2 \). For the whole region, \( x \) has to take all values from \( x = 0 \) to \( x = 1 \). Hence the region \( R \) of integration is given by
\( R \) : \( 0 \le x \le 1 \) , \( x^3 \le y \le - x^2 + 2 \)
Hence the integral may be calculated as follows
\( \displaystyle V = \int_0^1 \int_{x^3}^{-x^2+2} (x+y) \;dy \;dx = \dfrac{803}{420}\)
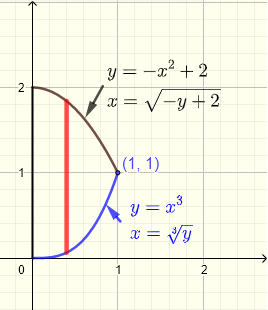
2) Using horizontal strips
A given horizontal strip starts on the \(y\)-axis \( x = 0 \) and ends either on the curve \( x = \sqrt[3]y \) or the curve \( x = \sqrt{- y+ 2} \). Because of the two different curves, region \( R \) may be split into two regions \( R_1 \) and \( R_2 \).
For region \( R_1 \), \( y \) has to take all values from \( y = 0 \) to \( y = 1 \) and for region \( R_2 \), \( y \) has to take all values from \( y = 1 \) to \( y = 2 \).
Hence the region \( R \) of integration has two parts:
\( R_1 \) : \( 0 \le x \le \sqrt[3]y \) , \( 0 \le y \le 1 \)
and
\( R_2 \) : \( 0 \le x \le \sqrt{- y+ 2} \) , \( 0 \le y \le 1 \)
Hence the integral may be calculated as follows
\( \displaystyle V = \iint_{R_1} (x+y) \;dx \;dy + \iint_{R_2} (x+y) \;dx \;dy \)
\( \displaystyle = \int_0^1 \int_{0}^{\sqrt[3]y} (x+y) \;dx \;dy + \int_1^2 \int_{0}^{\sqrt{-y+2}} (x+y) \;dx \;dy = \dfrac{803}{420}\)
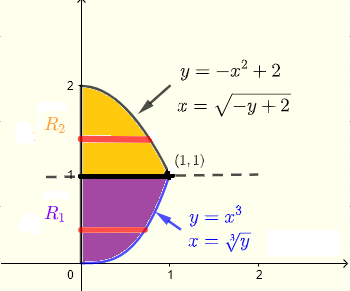
Examples where the Choice of the Order of Integration Depends on the Given Problem
In examples 3, 4 and 5, we show that sometimes we do not have the two choices of the order of integration that we usually have in double integrals.
The objectives of examples 3, 4 and 5 is to use graphs and diagrams to determine the order of integration that leads to the analytical calculation of double integral.
Example 3
Question: Evaluate the double integral \( \displaystyle V = \int _0^1 \int _y^1 (y + e^{-x^2}) dx dy \) if possible. Reverse the order of integration if it is necessary to evaluate the given integral.
Solution to Example 3
Let us start with the inner integral
Let
\( \displaystyle I = \int _y^1 (y+e^{-x^2}) dx \)
In trying to evaluate \( I \) above, the integral \( \displaystyle I = \int _y^1 (e^{-x^2}) dx \) cannot be done analytically.
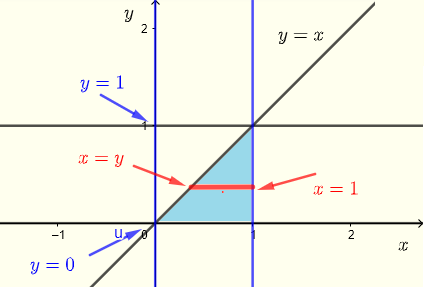
According to the limits of integrations given, the region \( R \) of integration of integral \( V \) may be written as
\( R \) : \( y \le x \le 1 \) , \( 0 \le y \le 1 \)
with the graph as shown below as a set of horizontal strips.
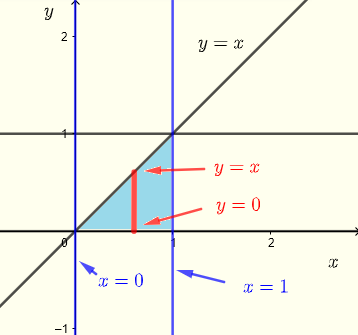
Let us now use vertical strips to describe region \( R \) as shown in the graph below.
\
Graph the region \( R \) of integration to see if by changing the order of integration, we can proceed further.
\( R \) : \( 0 \le x \le 1 \) , \( 0 \le y \le x \)
Integral \( V \) may be written as
\( \displaystyle V = \int _0^1 \int _0^x (y + e^{-x^2}) dy dx \)
Evaluate using the inner integral \( I \) given by
\( \displaystyle I = \int _0^x (y + e^{-x^2}) dy \)
\( = \left[ \dfrac{y^2}{2} + y e^{-x^2} \right]_0^x \)
\( = \dfrac{x^2}{2} + x e^{-x^2} \)
We now substitute \( I \) in \( V \) and calculate the given integral
\( \displaystyle V = \int _0^1 (\dfrac{x^2}{2} + x e^{-x^2} ) dx \)
\( = \left[ \frac{x^3}{6}-\frac{1}{2}e^{-x^2} \right]_0^1 \)
\( = \dfrac{2}{3} - \dfrac{1}{2}e^{-1} \)
Example 4
Evaluate the double integral \( \displaystyle V = \iint_R \left(\sqrt{1+y^3}+\:x\right)\:dy \:dx \) over the region \( R \) shaded in blue as shown below.
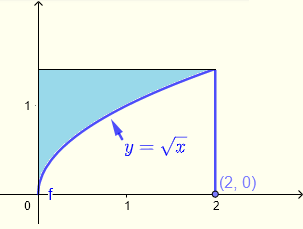
Solution to Example 4
Let the inner integral be \( \displaystyle I = \int \left(\sqrt{1+y^3}+\:x\right) \; dy \)
It can easily be seen that this integral is not easy to do analytically.
Let us interchange the order of integration.
\( V = \displaystyle \iint_R \left(\sqrt{1+y^3}+\:x\right)\:dx \:dy \)
Region \( R \) may be described by:
\( R\) : \( 0 \le x \le y^2 \) , \( 0 \le y \le \sqrt 2 \)
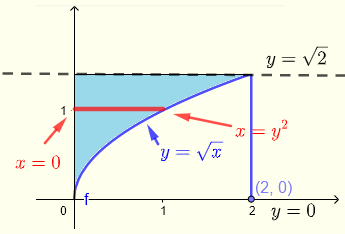
\( \displaystyle V = \int _0^{\sqrt 2} \int _0^{y^2} \left(\sqrt{1+y^3}+\:x\right) dx dy \)
Evaluate the inner integral \( I \).
\( I = \displaystyle \int _0^{y^2} \left(\sqrt{1+y^3}+\:x\right) dx \)
\( = \left [ x \sqrt{1+y^3} + \dfrac{x^2}{2} \right]_0^{y^2} \)
Evaluate and simplify
\( = y^2\sqrt{y^3+1}+\frac{y^4}{2} \)
Substitute \( I \) in \( V \) and calculate the outer integral
\( \displaystyle V = \int _{0\:}^{\sqrt 2} \left(y^2\sqrt{y^3+1}+\frac{y^4}{2} \right) \; dy \)
Calculate the above integral
\( \displaystyle V = \left [ \frac{2}{9}\left(y^3+1\right)^{\frac{3}{2}}+\frac{y^5}{10} \right]_0^{\sqrt 2} \)
Simplify
\( V = \frac{2}{9}\left(\left(\sqrt{2}\right)^3+1\right)^{\frac{3}{2}}+\frac{\left(\sqrt{2}\right)^5}{10}-\dfrac{2}{9} \approx 2.00 \)
Example 5
Evaluate the double integral \( \displaystyle V = \iint_R (x+y)\:dydx \) over the region \( R \) bounded by the curves of the equations \( x = (y-2)^2-2 \) and \( y = - x + 6 \)
Solution to Example 5
If vertical strips are used, the region of integration will have two parts because the limits of \( y \) are different in the intervals \( -2 \le x \le 2 \) and \( 2 \le x \le 7 \) and the calculations of the integral are very challenging.
We therefore use horizontal strips.
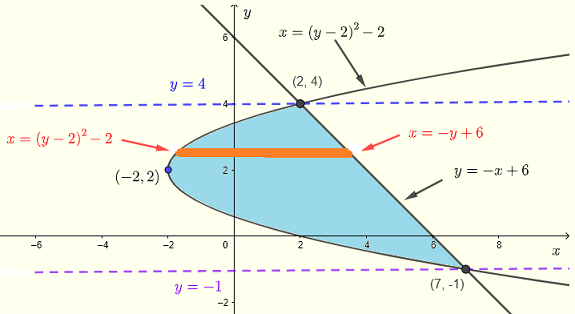
Region \( R \) may be described by:
\( R\) : \( (y-2)^2 - 2 \le x \le -y+6 \) , \( -1 \le y \le 4 \)
\( \displaystyle V = \int _{-1}^{4} \int _{(y-2)^2 - 2}^{-y+6} (x+y)\:dx \: dy \)
Let the inner integral be \( \displaystyle I = \int _{(y-2)^2 - 2}^{-y+6} (x+y)\:dx \)
Calculate the above integral
\( I = \dfrac{-y^4+6y^3-13y^2+12y+32}{2} \)
Substitute \( I \) in \( V \) and calculate the outer integral
\( \displaystyle V = \int _{-1}^4 \left( \dfrac{-y^4+6y^3-13y^2+12y+32}{2} \right) \; dy \)
Calculate the above integral
\( \displaystyle V = \dfrac{1}{2} \left[-\dfrac{y^5}{5}+\dfrac{3y^4}{2}-\dfrac{13y^3}{3}+6y^2+32y\right]_{-1}^4 \)
Evaluate
\( V = \dfrac{875}{12} \)
Note
As an exercise show that using vertical strips, the double integral is given by:
\( \displaystyle \int _{-2}^2\:\int _{2-\sqrt{x+2}}^{2+\sqrt{x+2}}\:\left(x+y\right)dydx+\int _2^7\:\int _{2-\sqrt{x+2}}^{-x+6}\:\left(x+y\right)dydx \)
More Questions with Answers
Part 1
-
Write the limits of the double integral \( \displaystyle V = \iint_R x y \;dy \;dx \) and \( \displaystyle V = \iint_R x y \;dx \;dy \) where the region \( R \) is on the \( xy\)-plane such that \(x \ge 0\) and \(y \ge 0\) and bounded by the curve whose equation is given by
\( x^2 + y^2 = 1 \) and evaluate it.
-
Write the limits of the double integral \( \displaystyle V = \iint_R \sin(x^2) \;dy \;dx \) and \( \displaystyle V = \iint_R \sin(x^2) \;dx \;dy \) where the region \( R \) is a triangle with vertices at the points \( A(0,0)\) , \( B(3,0) \) and \( C(3,3) \) and evaluate it.
Part 2
Evaluate \( \displaystyle V = \int _0^1 \int _{ \arcsin y}^{\frac{\pi }{2}}\:\left(xy\right)dxdy \)
Answers to the Above Questions
Part 1:
-
Region of integration
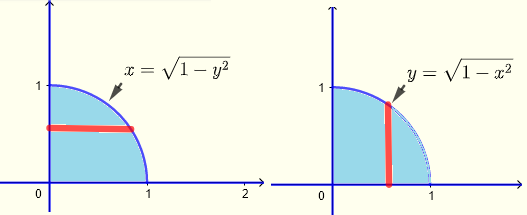
Vertical strips
\( 0 \le x \le 1 \) , \( 0 \le y \le \sqrt{1-x^2} \)
\( \displaystyle \int _0^1\:\int _0^{\sqrt{1-x^2}}\:xy\:dy\:dx = 1/8 \)
Horizontal strips
\( 0 \le x \le \sqrt{1-y^2} \) , \( 0 \le y \le 1 \)
\( \displaystyle \int _0^1\:\int _0^{\sqrt{1-y^2}}\:xy\:dx\:dy = 1/8\)
-
Region of integration

Vertical strips
\( 0 \le x \le 3\) , \( 0 \le y \le x \)
\( \displaystyle \int _0^3\:\int _0^x \:\sin(x^2)\:dy\:dx = \dfrac{1}{2}\left(-\cos \left(9\right)+1\right) \)
Horizontal strips
\( y \le x \le 3 \) , \( 0 \le y \le 3 \)
\( \displaystyle \int _y^3\:\int _0^3\:\sin(x^2)\:dx\:dy \) Very challenging to solve analytically.
Part 2
\( \displaystyle V = \int _0^1 \int _{ \arcsin y}^{\frac{\pi }{2}}\:\left(xy\right)dxdy \)
Calculate the inner integral \( I \) given by
\( \displaystyle I = \int _{ \arcsin y}^{\frac{\pi }{2}}\:\left(xy\right)dx \)
\( = y \left(\dfrac{\pi^2}{8} - \dfrac{\arcsin^2(y)}{2} \right) \)
We now substitute \( I \) by its expression in the integral \( V \)
\( \displaystyle V = \int _0^1 (y \left(\dfrac{\pi^2}{8} - \dfrac{\arcsin^2(y)}{2} \right)) dy \)
which is challenging to do analytically.
Let us restart and now interchange the order of integration
Let us first graph the region \( R \) of integration
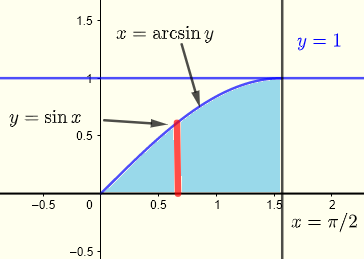
\( \displaystyle V = \int _0^{\frac{\pi }{2}} \int _0^{\sin x} x \; y \; dy \;dx \)
Let the inner integral \( I = \int _0^{\sin x} x \; y \; dy \)
Calculate \( I \)
\( I = x\frac{\sin ^2\left(x\right)}{2} \)
\( \sin^2(x) = \dfrac{1-\cos(2x)}{2} \)
\( I = \dfrac{x}{4}(1-cos(2x) \)
Substitute \( I \) in \( V \)
\( \displaystyle V = \int _0^{\frac{\pi }{2}} (\dfrac {x}{4} - \dfrac {x}{4} \cos (2x) ) dx \)
Split the integrand
\( \displaystyle = \int _0^{\frac{\pi }{2}} \dfrac {x}{4} dx - \int _0^{\frac{\pi }{2}} \dfrac {x}{4} \cos (2x) dx \)
The integral on the right is done using the technique of integration by parts to obtain
\( = \left[ \frac{x^2}{8} \right]_0^{\pi/2}- \left[\frac{1}{8} x \sin (2x)+\frac{1}{16}\cos (2x) \right]_0^{\pi/2} \)
Evaluate
\( = \dfrac{\pi^2+4}{32} \)
More References and Links
- Double Integrals Calculations
- Howard Anton, Irl C. Bivens, Stephen Davis ; Calculus: Early Transcendentals; Willey, 2012.
- Gilbert Strang; MIT, Calculus, Wellesley-Cambridge Press, 1991
- Joel Hass, University of California, Davis; Maurice D. Weir Naval Postgraduate School; George B. Thomas, Jr.Massachusetts Institute of Technology ; University Calculus , Early Transcendentals, Third Edition
, Boston Columbus , 2016, Pearson.
Engineering Mathematics with Examples and Solutions