Double Integrals in Polar Coordinates

Examples of how to calculate double integrals in polar coordinates and general regions of integration are presented along with their detailed solutions. The examples also show that converting double integrals from rectangular to polar coordinates may make it less challenging to evaluate using elementary functions.

Convert Double Integrals in Polar Coordinates

The change of double integrals from Cartesian (or rectangular) to polar coordinates is given by [1]
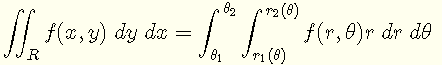
Double Integral in Polar Coordinates

with the relationships between the rectangular coordinates x and y; and the polar coordinates r and θ are given by [6]

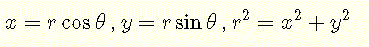
The area A of a closed region R described in polar coordinates is given by
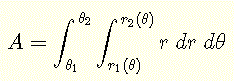
Area in Double Integral in Polar Coordinates

Examples with Detailed Solutions

Example 1 \( \) \( \) \( \) \( \)
Question: Calculate the double integral \( \displaystyle V = \iint_R \sqrt {1 - x^2 - y^2} \;dy \;dx \) where the region \( R \) is the surface enclosed by a circle on the plane \( xy\)-plane with center at the origin and radius equal to \( 1\).
Solution to Example 1
The given integral is in rectangular coordinates and cannot be done using elementary functions. Let us try to convert to polar coordinates.
Let \( f(x,y) = \sqrt {1 - x^2 - y^2} \) and express it in polar coordinates.

graph of f(x,y) example 1

\( r^2 = x^2 + y^2 \)
Hence function \( f(x,y) \) in polar form is given by
\( f(r,\theta) = \sqrt {1 - r^2} \)
Region \( R \) of integration is a circle and may be defined by inequalities as follows:
\( R: \) \( 0 \le \theta \le 2\pi \) and \( 0 \le r \le 1 \)
circular region in polar coordinates example 1
The given integral in rectangular coordinates may be converted to polar coordinates as follows
\( \displaystyle V = \iint_R \sqrt {1 - x^2 - y^2} \;dy \;dx = \int_0^{2\pi} \int_0^{1} \sqrt{1-r^2} \; r \; dr \; d\theta \)
Let \( I \) be the inner integral defined by
\( \displaystyle I = \int_0^{1} \sqrt{1-r^2} \; r \; dr \)
\( = \left[ -\frac{1}{3}\left(1-r^2\right)^{\frac{3}{2}} \right]_0^1 = \dfrac{1}{3} \)
Substitute \( I \) and calculate \( V \)
\( \displaystyle V = \int_0^{2\pi} (1/3) \; d\theta \)
\( = \dfrac{1}{3} \left[ \theta \right]_0^{2\pi} \)
\( = \dfrac{2\pi}{3} \)

Example 2
Question: Calculate the double integral \( \displaystyle V = \int_0^{1} \int_0^{\sqrt{1-x^2}} e^{x^2+y^2} \; dy \; dx \)
Solution to Example 2
The given integral cannot be easily calculated in rectangular coordinates hence the need to use polar coordinates instead which may make easy to evaluate.
Let us express \( f(x,y) = e^{x^2+y^2} \) in polar coordinates.
\( r^2 = x^2 + y^2 \)
Hence the function \( f(x,y) \) in polar form is given by
\( f(r,\theta) = e^{r^2} \)
In rectangular coordinates, the region \( R \) of integration is defined by the given limits of integration.
\( R: \) \( 0 \le x \le 1 \) and \( 0 \le y \le \sqrt{1-x^2} \)
Let us solve the inequality \( y \le \sqrt{1-x^2} \) graphically
Square both sides of the inequality
\( y^2 \le 1-x^2 \)
Rewrite with terms in \( x \) and \( y \) on the left side
\( y^2 + x^2 \le 1 \)
The above inequality is the set of all points \( (x,y) \) inside or on the circle with center at the origin \( (0,0) \) and radius \( 1 \)
Putting all inequalities together, the region of integration \( R \) is shown below.
region in Cartesian coordinates example 2
The above region in polar form is shown below
region in polar coordinates example 2
and is defined by the inequalities
\( R: \) \( 0 \le \theta \le \pi/2 \) and \( 0 \le r \le 1 \)
The integral may now be converted in polar coordinates as follows
\( \displaystyle V = \int_0^{1} \int_0^{\sqrt{1-x^2}} e^{x^2+y^2} \; dy \; dx = \int_0^{\pi/2} \int_0^1 e^{r^2} r \; dr \; d\theta \)
Let \( I \) be the inner integral defined by
\( \displaystyle I = \int_0^1 e^{r^2} r \; dr \)
\( = \left[ \dfrac{1}{2} e{r^2} \right]_0^1 \)
\( = \dfrac{1}{2} (e - 1) \)
Substitute \( I \) into \( V \)
\( \displaystyle V = \int_0^{\pi/2} \dfrac{1}{2} (e - 1) \; d\theta \)
\( = \dfrac{\pi}{4} (e - 1) \)

Example 3
Question: Express the integral \( \displaystyle V = \iint_R {x^2+y^2} \; dy \; dx \) where \( R \) is a circle on the \( xy \) plane with center at the point \( (1,0) \) and a radius equal to \( 1 \) using Cartesian (or rectangular) and polar coordinates? Evaluate the integral. Evaluate the integral.
Solution to Example 3
We first graph the region of integration \( R \) and define it in terms of rectangular and polar coordinates.
1) Rectangular coordinates
The equation of the circle with center at \( (1,0) \) and radius equal to \( 1 \) is given by
\( (x-1)^2 + y^2 = 1 \)
Expand and group like terms
\( x^2 - 2x + y^2 = 0 \)
Solve the above equation for y to obtain two solutions
\( y = \pm \sqrt {2x-x^2} \)
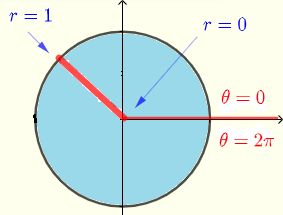
Using vertical strips, the region \( R \) may be described by the inequalities
\( R: \) \( 0 \le x \le 2 \) and \( - \sqrt {2x-x^2} \le y \le \sqrt {2x-x^2} \)
region in Cartesian coordinates example 3
The integral may be written as
\( \displaystyle V = \int_0^2 \int_{-\sqrt {2x-x^2}}^{\sqrt {2x-x^2}} \; \; (x^2+y^2) \; dy \; dx \)
Let \( I_1 \) be the inner integral given by
\( \displaystyle I_1 = \int_{-\sqrt {2x-x^2}}^{\sqrt {2x-x^2}} \; \; (x^2+y^2) \; dy \)
Evaluate \( I_1 \)
\( \displaystyle I_1 = 2x^2\sqrt{2x-x^2}+2\cdot \frac{\left(2x-x^2\right)^{\frac{3}{2}}}{3} \)
The next step to calculate the outer integral above integral in rectangular coordinates is a challenging one.

2) Polar coordinates
Using strips from the origin to a point on the circle: at the origin \( r = 0 \); on the circle \( r = \sqrt {x^2 + y^2} \)
Let us convert the equation of the circle, \( x^2 + y^2 = 2x \) in polar form.
From relationship between rectangular and polar coordinates [6], we have
\( r^2 = x^2 + y^2 \) and \( x = r \cos \theta \)
Substitute \( x^2 + y^2 \) by \( r^2 \) and \( x \) by \( r \cos \theta \) in the equation \( x^2 + y^2 = 2x \) to obtain
\( r^2 = 2 r \cos \theta \)
Divide both sides of the above equation by \( r \)
\( r = 2 \cos \theta \)
In polar coordinates, the region \( R \) may be described by the inequalities
\( R: \) \( -\pi/2 \le \theta \le \pi/2 \) and \( 0 \le r \le 2 \cos \theta \)
region in polar coordinates example 3

Use \( r^2 = x^2 + y^2 \) to write the integral in polar form as
\( \displaystyle V = \int_{-\pi/2}^{\pi/2} \int_{0}^{2 \cos \theta} r^2 \; r \; dr \; d\theta \)
Let the innner integral \(I \) be defined by
\( \displaystyle I = \int_{0}^{2 \cos \theta} r^2 \; r \; dr \)
Evaluate
\( \displaystyle I = \left[ r^4 / 4 \right]_{0}^{2 \cos \theta} \)
\( \displaystyle I = 4 cos^4 \theta \) (eq 1)
Reduce the power in the above expression \( \cos^4 \theta \)
\( \cos^4 \theta = \cos^2 \theta \cos^2 \theta \)
Use the power reducing identity
\( \cos^2 \theta = \dfrac{cos (2\theta) + 1}{2} \)
Hence
\( \cos^4 \theta = \left( \dfrac{\cos (2\theta) + 1}{2} \right)^2 \)
\( = \dfrac{\cos^2(2\theta) + 2 \cos (2\theta) + 1}{4} \)
Use the power reducing identity one more time to obtain
\( \cos^4 \theta = \dfrac{\cos(4\theta) + 4\cos(2\theta) }{8} + 3/8 \)
We now substitute the above expression in (eq 1) to obtain
\( I = \dfrac{\cos(4\theta) + 4\cos(2\theta) }{2} + 3/2 \)
Substitute \( I \) in the integral and evaluate
\( \displaystyle V = \int_{-\pi/2}^{\pi/2} (\dfrac{\cos(4\theta) + 4\cos(2\theta) }{2} + 3/2 ) \; d\theta \)
\( \displaystyle = \left[ \frac{1}{2}\left(\frac{1}{4}\sin \left(4\theta\right)+2\sin \left(2\theta\right)\right)+\frac{3}{2}\theta \right]_{-\pi/2}^{\pi/2} \)
\( = \dfrac{3\pi}{2} \)
The given integral is much easier evaluated using polar coordinates.

Example 4
Question: Change the integral \( \displaystyle V = \int_{-1}^0 \int_{-\sqrt{1-x^2}}^0 \dfrac{\sqrt{x^2+y^2}}{1+\sqrt{x^2+y^2}} \; dy \; dx \) into polar coordinates and evaluate it.
Solution to Example 4
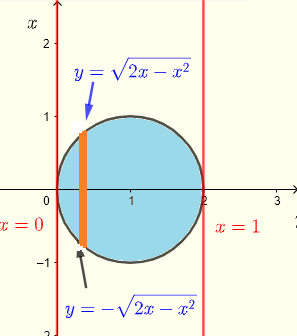
From the limits of integration in rectangular coordinates, we deduce the region \( R \) of integration which is a quarter of a circle in quadrant III as
\( R: \) \( 0 \le x \le 2 \) and \( - \sqrt {1-x^2} \le y \le 0 \)
and its graph as shown below
region in Cartesian coordinates example 4
In polar Polar coordinates using strips from the origin to a point on the quarter of a circle: at the origin \( r = 0 \). On the circle \( r = 1 \), the region \( R \) of integration in polar coordinates may be defined as
\( R: \) \( \pi \le \theta \le 3\pi/2 \) and \( 0 \le r \le 1 \)
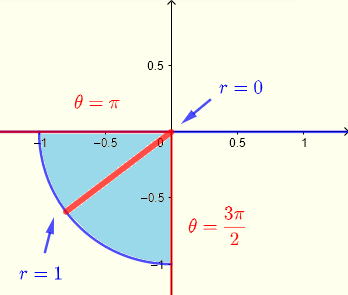
region in polar coordinates example 4

Use \( r = \sqrt { x^2 + y^2 } \) to write the given integral in polar form as
\( \displaystyle V = \int_{\pi}^{3\pi/2} \int_{0}^{1} \dfrac{r}{1+r} \; r \; dr \; d\theta \)
\( \displaystyle = \int_{\pi}^{3\pi/2} \int_{0}^{1} \dfrac{r^2}{1+r} \; dr \; d\theta \)
Use division to expand the integrand \( \dfrac{r^2}{1+r} \) as follows
\( \dfrac{r^2}{1+r} = r-1+\frac{1}{r+1} \)
Substitute the integrand in expanded for in the integral
\( \displaystyle V = \int_{\pi}^{3\pi/2} \int_{0}^{1} (r-1+\frac{1}{r+1}) \; dr \; d\theta \)
Integrate
\( \displaystyle = \int_{\pi}^{3\pi/2} \left[ \dfrac{r^2}{2} - r + ln |r+1| \right]_0^1 d\theta \)
Evaluate
\( \displaystyle = \int_{\pi}^{3\pi/2} (\ln (2)-\dfrac{1}{2}) d\theta \)
Integrate
\( = \left( \ln (2)-\dfrac{1}{2} \right) \left[ \; \theta \; \right]_{\pi}^{3\pi/2} \)
Evaluate
\( V = \dfrac{\pi}{2} \left( \ln (2)-\dfrac{1}{2} \right) \)

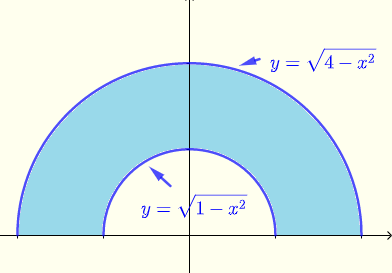
Answers to the Above Questions

Part 1:

Region of integration in rectangular (left side) given by the limits of integration and polar (right side) coordinates are shown below.

\( \displaystyle V = \int_{-1}^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \; \; \sin(x^2+y^2) \;dy \;dx \)
Convert the above integral in polar coordinates
\( \displaystyle V = \int_{0}^{2\pi} \int_0^1 \; \; \sin(r^2) \;r \; dr \;d\theta \)
Evaluate
\( = \pi (1 -\cos 1) \)
Region of integration in rectangular (left side) given by the limits of integration and polar (right side) coordinates are shown below.

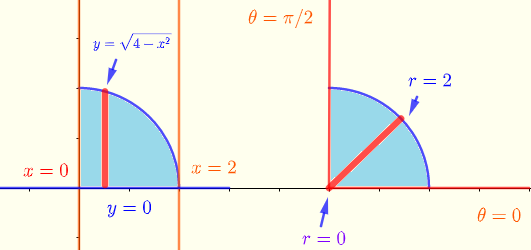
\( \displaystyle V = \int _0^2\:\:\int _0^{\sqrt{4-x^2}} \sqrt{x^2+y^2} \:\;dy\:\;dx\: \)
Convert the above integral in polar coordinates
\( \displaystyle V = \int_{0}^{\pi/2} \int_0^2 \; \; r^2 \; dr \;d\theta \)
Evaluate
\( = \dfrac{4\pi }{3} \)

Part 2
Evaluate the given integral using rectangular coordinates
\( \displaystyle V = \int_{-2}^{2} \int_0^{\sqrt{4-x^2}} \: e^{\sqrt{x^2+y^2}} \; dy \; dx - \int_{-1}^{1} \int_0^{\sqrt{1-x^2}} \: e^{\sqrt{x^2+y^2}} \; dy \; dx \)
which is quite challenging using elementary functions.
Region of integration in polar coordinates shown below

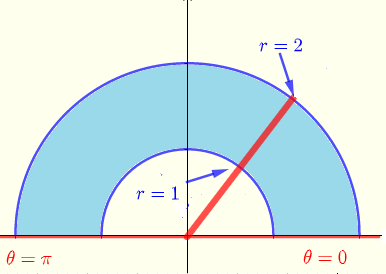
region of integration in polar coordinates for exercise 3

\( R: \) \( 0 \le \theta \le \pi \) and \( 1 \le r \le 2 \)
Given
\( \displaystyle V = \iint_R \: e^{\sqrt{x^2+y^2}} \; dx \; dy \)
The given integral in polar coordinates is given by
\( \displaystyle V = \int_0^{\pi} \; \int_1^2 \: r e^{r} \; dr \; d\theta \)
Evaluate
\( = \pi e^2 \)

Double Integrals in Polar Coordinates

Convert Double Integrals in Polar Coordinates

Examples with Detailed Solutions

More Questions with Answers

Answers to the Above Questions

More References and Links