3D GPS Calculator: Distance and Angle Between Two Points in Space Using GPS Coordinates
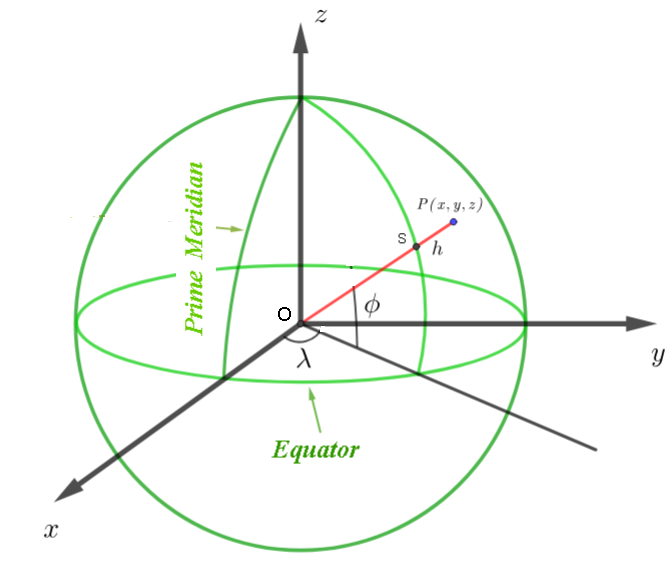
GPS Coordinates
- \(\phi\) = Latitude, \(\lambda\) = Longitude, \( h \) = height above sea level
- Uses WGS 84 ellipsoid model (not spherical)
- ECEF coordinates in meters
WGS 84 Parameters
| Parameter | Description | Value |
|---|---|---|
| \( a \) | Semi-major axis | 6,378,137 m |
| \( f \) | Flattening | \(\frac{1}{298.257223563}\) |
| \( e^2 \) | Square of eccentricity | 0.00669437999014 |
| \( b \) | Semi-minor axis | \( a(1 - f) \approx 6,356,752.3142 \, \text{m} \) |
LLH to ECEF Conversion
Prime Vertical Radius of Curvature
\[ N = \frac{a}{\sqrt{1 - e^2 \sin^2 \phi}} \]ECEF Coordinates
\[ \begin{aligned} X &= (N + h) \cos \phi \cos \lambda \\ Y &= (N + h) \cos \phi \sin \lambda \\ Z &= \left(N(1 - e^2) + h\right) \sin \phi \end{aligned} \]Distance Between Points
\[
\text{Distance} = \sqrt{(X_B - X_A)^2 + (Y_B - Y_A)^2 + (Z_B - Z_A)^2}
\]
Angle Between Vectors
\[
\theta = \arccos\left(\frac{\vec{OA} \cdot \vec{OB}}{\|\vec{OA}\| \|\vec{OB}\|}\right)
\]
\[
\vec{OA} \cdot \vec{OB} = X_A X_B + Y_A Y_B + Z_A Z_B
\]
Area of Triangle OAB
\[
\text{Area} = \frac{1}{2} \|\vec{OA} \times \vec{OB}\|
\]
\[
\|\vec{OA} \times \vec{OB}\| = \sqrt{(Y_A Z_B - Z_A Y_B)^2 + (X_A Z_B - Z_A X_B)^2 + (X_A Y_B - Y_A X_B)^2}
\]