여러 변수 함수와 이러한 함수의 정의역 개념이 예제와 함께 설명됩니다. 문제와 그 해결책도 포함되어 있습니다.
두 변수의 부등식 시스템을 푸는 기술은 두 변수 함수를 찾는 데 필요합니다.
잘 알려진 공식 몇 가지를 살펴보겠습니다.
a) 한 변의 길이가 \( x \)인 정사각형의 둘레 \( P \)는 \( P = 4x \)로 주어집니다.
b) 길이가 \( L \), 너비가 \( W \)인 직사각형의 면적 \( A \)는 \( A = LW \)로 주어집니다.
c) 뉴턴의 만유인력 법칙에 따른 두 물체의 질량 \( m_1 \)과 \( m_2 \), 그리고 거리가 \( d \)일 때의 힘 \( F \)는 \( F = G \dfrac{m_1 m_2}{d^2} \)로 주어집니다.
여기서 \( G \)는 상수입니다.
위의 예에서:
a)의 둘레 \( P \)는 변수 \( x \)의 단일 변수 함수입니다.
b)의 면적 \( A \)는 \( L \)과 \( W \)의 두 변수 함수입니다.
c)의 힘 \( F \)는 \( m_1 \), \( m_2 \), \( d \)의 세 변수 함수입니다 (참고: \( G \)는 상수입니다).
\( n \)개의 변수 \( x_1, x_2, ...., x_n \)의 함수 \( f \)는 각각의 \( x_1, x_2, ...., x_n \)에 대해 고유한 실수 \( f(x_1, x_2, ...., x_n) \)를 할당하는 규칙입니다.
함수 \( f \)가 고유한 실수 값을 가지는 모든 \( x_1, x_2, ...., x_n \)의 n-튜플 집합 \( D \)를 함수 \( f \)의 정의역이라고 합니다.
\( u = f(x_1, x_2, ...., x_n) \)라고 할 때, \( D \)의 모든 \( x_1, x_2, ...., x_n \)에 해당하는 \( u \)의 모든 값의 집합을 \( f \)의 치역이라고 합니다 [1], [2], [3].
예제 1 두 변수의 함수
함수 \( f \)가 다음과 같이 정의된다고 하자.
\[ f(x,y) = \sqrt{x^2+y^2} + \ln(x-y) \]
a) 다음 값을 계산하시오: \( f(4,3) \), \( f(e^2,0) \)
b) 함수 \( f \)의 정의역을 찾고 그래프로 나타내시오.
예제 1의 해답
a)
\( f(4,3) \)를 계산하기 위해 \( x \)에 \( 4 \)를, \( y \)에 \( 3 \)을 대입합니다.
따라서
\( f(4,3) = \sqrt{4^2+3^2} + \ln(4-3) \)
간단히 정리하면
\( \quad = \sqrt{25} + \ln(1) = 5 + 0 = 5 \)
\( f(e^2,0) \)를 계산하기 위해 \( x \)에 \( e^2 \), \( y \)에 \( 0 \)을 대입합니다.
따라서
\( f(e^2,0) = \sqrt{e^2 + 0^2} + \ln(e^2 - 0) \)
간단히 정리하면
\( \quad = e + 2 \)
b)
함수 \( f(x,y) \)의 정의역을 찾기 위해 다음 조건을 설정합니다:
1) \( \quad x^2+y^2 \ge 0 \), 제곱근 안의 값은 음수가 되어서는 안 됩니다.
2) \( \quad x - y \gt 0 \), 로그의 인수는 양수여야 합니다.
위의 조건 1)은 항상 만족합니다.
조건 2)의 부등식은 그래프로 나타내어 아래 그래프와 같이 해를 얻을 수 있습니다.

예제 2 세 변수의 함수
함수 \( g \)가 다음과 같이 정의된다고 하자.
\[ g(x,y,z) = \sqrt{ x^2 + y^2 + z^2 - 9} \]
a) 다음 값을 계산하시오: \( g(3,-1,1) \), \( g(3/2,1/4,7/2) \)
b) 함수 \( g \)의 정의역을 찾고 설명하시오.
예제 2의 해답
a)
\( g(3,-1,1) \)를 계산하기 위해 \( x \)에 \( 3 \), \( y \)에 \( -1 \), \( z \)에 \( 1 \)을 대입합니다.
따라서
\( g(3,-1,1) = \sqrt{ 3^2 + (-1)^2 + 1^2 - 9} \)
간단히 정리하면
\( \quad = \sqrt{2} \)
\( g(3/2,1/4,7/2) \)를 계산하기 위해 \( x \)에 \( 3/2 \), \( y \)에 \( 1/4 \), \( z \)에 \( 7/2 \)을 대입합니다.
따라서
\( g(3/2,1/4,2) = \sqrt{ (3/2)^2 + (1/4)^2 + (7/2)^2 - 9} \)
간단히 정리하면
\( \quad = \dfrac{\sqrt{89}}{4} \)
b)
함수 \( g(x,y,z) \)의 정의역을 찾기 위해 다음 조건을 설정합니다:
\( x^2 + y^2 + z^2 - 9 \ge 0 \) , 제곱근 안의 값은 음수가 되어서는 안 됩니다.
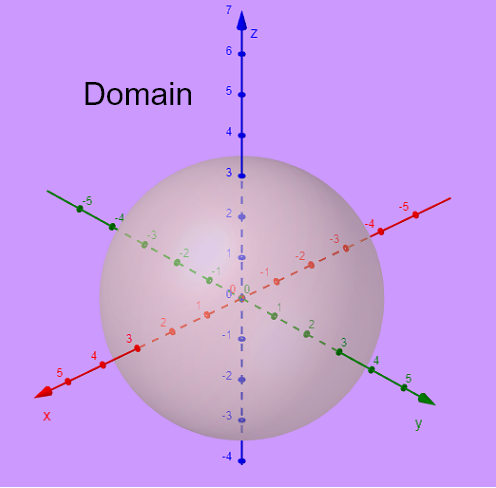
식 \( x^2 + y^2 + z^2 - 9 = 0 \)은 \( x^2 + y^2 + z^2 = 3^2 \)로 표현할 수 있습니다.
따라서 식 \( x^2 + y^2 + z^2 - 9 = 0 \)의 그래프는 반지름이 \( 3 \)이고 중심이 원점 \( (0,0,0) \)에 있는 구로 나타납니다.
예제 3 두 변수의 함수
함수 \( h \)가 다음과 같이 정의된다고 하자.
\[ h(x,y) = \dfrac{1}{\ln (1 - x y) } - \sqrt{x - y^2}\]
a) 함수 \( h \)의 정의역을 찾고 설명하시오.
b) 정의역에 속하는 \( (x,y) \)의 예를 3개 들고 이 점들에서의 함수 값을 계산하시오.
c) 정의역에 속하지 않는 \( (x,y) \)의 예를 3개 들으시오.
예제 3의 해답
a)
함수 \( h(x,y) \)의 정의역을 찾기 위해 다음 조건을 설정합니다:
1) \( \quad 1 - x y \gt 0 \) , 로그의 인수는 양수여야 합니다.
2) \( \quad x - y^2 \ge 0 \) , 제곱근 안의 값은 음수가 되어서는 안 됩니다.
3) \( \quad \ln (1 - x y) \ne 0 \) 또는 \( 1 - xy \ne 1 \) 이는 \( xy \ne 0 \)와 동등하며, 분모 \( \ln (1 - x y) \)는 0이 될 수 없습니다.
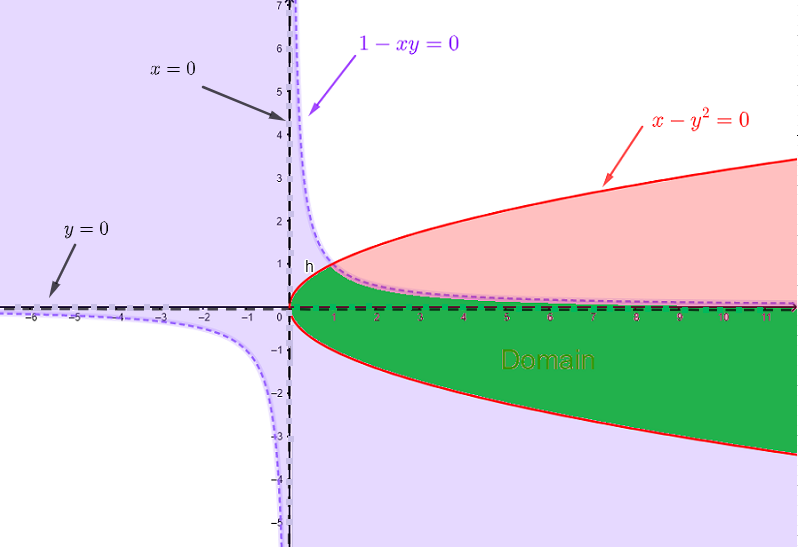
조건 1)은 \( 1 - x y = 0 \) 또는 \( y = \dfrac{1}{x} \)을 그래프로 나타내어 \( 1 - x y \gt 0 \)을 만족하는 점들의 집합을 선택하여 해결합니다 (연보라색).
조건 2)은 \( x - y^2 = 0 \) 또는 \( x = y^2 \)를 그래프로 나타내어 \( x - y^2 \ge 0 \)을 만족하는 점들의 집합을 선택하여 해결합니다 (빨간색).
조건 3)은 축 위의 어떤 점도 포함하지 않습니다 (축 위의 점선).
정의역은 조건 1), 2) 및 3)에서 찾은 모든 세트의 교집합이며, 아래 그래프에서 녹색으로 표시된 영역이 정의역입니다.
Part A
다음 함수들이 주어졌을 때:
\( f (x,y) = \dfrac{1}{\sqrt{x^2 - y}} \)와 \( g (x,y) = \ln (x^2 + y^2 - 1) \)
a) 각 함수의 정의역을 찾으시오.
b) 다음을 계산하시오:
1) \( f (1,0) \) , 2) \( g (1,-1) \) , 3) \( \dfrac{f(3,4)}{g(2,0)} \)
Part B
전기 회로에서, 병렬로 연결된 세 개의 저항기 \( r_1, r_2, r_3 \)의 저항 \( R \)은 다음과 같이 주어집니다.
\( \dfrac{1}{R} = \dfrac{1}{r_1} + \dfrac{1}{r_2} + \dfrac{1}{r_3} \)
a) \( R \)을 변수 \( r_1, r_2, r_3 \)의 함수로 표현하시오.
b) \( r_1 = 100 \), \( r_2 = 50 \), \( r_3 = 20 \)일 때 \( R \)을 계산하시오.
Part C
다음 함수들의 정의역을 찾으시오:
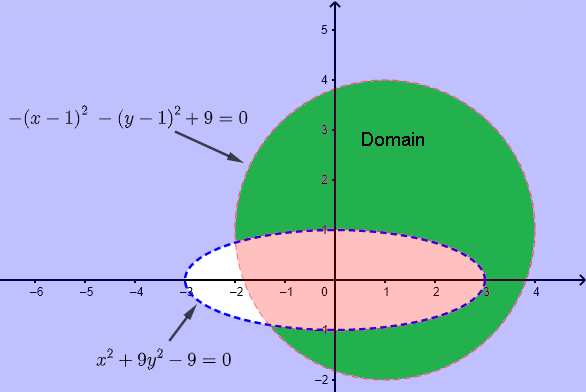
a) \( f(x,y) = \sqrt{x^2+y-2x} \)
b) \( h(x,y) = \dfrac{\ln(x^2+9 y^2-9)}{\sqrt{7-x^2-y^2+2 x + 2 y}} \)
Part A
\( f (x,y) = \dfrac{1}{\sqrt{x^2 - y}} \)와 \( g (x,y) = \ln (x^2 + y^2 - 1) \)
a)
함수 \( f \)의 정의역은 다음 부등식을 풀어 찾습니다: \( x^2 - y \gt 0 \); 분모가 0이 되어서는 안 되고 제곱근 안의 인수는 음수가 되어서는 안 됩니다.
식 \( y = x^2 \)을 그래프로 나타내고 \( x^2 - y \gt 0 \)을 만족하는 영역을 선택합니다. 그래프적 해결책은 아래와 같습니다. 정의역은 포물선 \( y = x^2 \) 바깥의 모든 점들의 집합입니다.

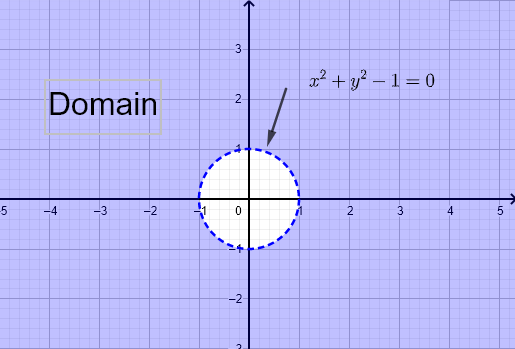
Part B
a)
\( \dfrac{1}{R} = \dfrac{1}{r_1} + \dfrac{1}{r_2} + \dfrac{1}{r_3} \)이 주어졌을 때,
모든 항에 \( r_1 r_2 r_3 \)를 곱합니다.
\( \dfrac{r_1 r_2 r_3}{R} = \dfrac{r_1 r_2 r_3}{r_1} + \dfrac{r_1 r_2 r_3}{r_2} + \dfrac{r_1 r_2 r_3}{r_3} \)
간단히 정리하면
\( \dfrac{r_1 r_2 r_3}{R} = r_2 r_3 + r_1 r_3 + r_1 r_2 \)
\( R \)에 대해 풀어봅니다.
\( R(r_1,r_2,r_3) = \dfrac{r_1 r_2 r_3}{r_2 r_3 + r_1 r_3 + r_1 r_2} \)
b)
\( R(100,50,20) = \dfrac{100 \times 50 \times 20}{50 \times 20 + 100 \times 20 + 100 \times 50} = 12.5\)
Part C
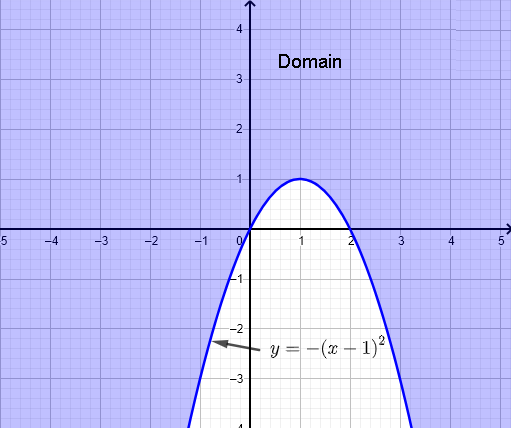
a) \( f(x,y) = \sqrt{x^2+y-2x} \)
함수 \( f(x,y) \)는 제곱근의 인수가 음수가 되지 않는다면 실수 값을 가집니다. 따라서 조건은 다음과 같습니다.
\( x^2+y-2x \ge 0 \)
완전제곱식으로 변환하여 다시 씁니다.
\( (x-1)^2 - 1 + y \ge 0 \)
\( y \ge - (x-1)^2 + 1 \)
포물선 \( y = - (x-1)^2 + 1 \)을 그래프로 나타내고, 함수 \( f \)의 정의역을 찾습니다.
정의역은 포물선 \( y = - (x-1)^2 + 1 \) 위나 밖의 점들 \( (x,y) \)의 집합입니다. (보라색)