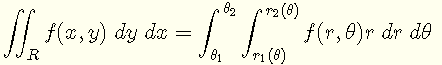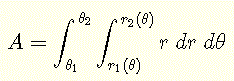목차
극좌표에서의 이중 적분
극좌표 와 일반적인 영역 의 이중 적분을 계산하는 방법에 대한 예제와 상세한 해결책이 제시됩니다. 예제는 또한 직사각형 좌표에서 극좌표로의 변환은 기본 함수를 사용하여 계산하는 것이 더 쉬울 수 있음을 보여줍니다.
극좌표에서의 이중 적분 변환
직교 좌표 (또는 직사각형 좌표)에서 극좌표로의 이중 적분 변환은 다음과 같습니다 [1]
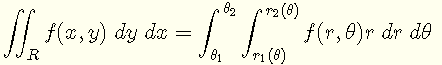
직교 좌표 x와 y; 그리고 극좌표 r과 θ 간의 관계는 다음과 같습니다 [6]
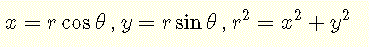
극좌표로 설명된 닫힌 영역 R의 영역 A는 다음과 같습니다.
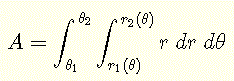
상세한 해결책을 가진 예제
예제 1
\( \) \( \) \( \) \( \)
문제: \( \displaystyle V = \iint_R \sqrt {1 - x^2 - y^2} \;dy \;dx \) 를 계산하십시오. 여기서 영역 \( R \)은 원점을 중심으로 하고 반지름이 \( 1\)인 평면 \( xy \) 평면의 원에 의해 둘러싸인 면입니다.
예제 1의 해결책
주어진 적분은 직사각형 좌표로 되어 있으며 기본 함수를 사용하여 계산할 수 없습니다. 극좌표로 변환해 보겠습니다.
\( f(x,y) = \sqrt {1 - x^2 - y^2} \) 이고 이를 극좌표로 표현합니다.
-example-1.gif)
\( r^2 = x^2 + y^2 \)
따라서 극형태로 함수 \( f(x,y) \)는 다음과 같이 주어집니다.
\( f(r,\theta) = \sqrt {1 - r^2} \)
적분 영역 \( R \)은 원이며 다음과 같은 부등식으로 정의할 수 있습니다:
\( R: \) \( 0 \le \theta \le 2\pi \) 그리고 \( 0 \le r \le 1 \)
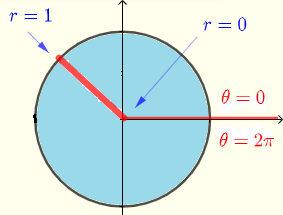
직교 좌표에서 주어진 적분은 다음과 같이 극좌표로 변환될 수 있습니다.
\( \displaystyle V = \iint_R \sqrt {1 - x^2 - y^2} \;dy \;dx = \int_0^{2\pi} \int_0^{1} \sqrt{1-r^2} \; r \; dr \; d\theta \)
\( I \)를 내부 적분으로 정의합시다.
\( \displaystyle I = \int_0^{1} \sqrt{1-r^2} \; r \; dr \)
\( = \left[ -\frac{1}{3}\left(1-r^2\right)^{\frac{3}{2}} \right]_0^1 = \dfrac{1}{3} \)
\( I \)를 대입하고 \( V \)를 계산하십시오.
\( \displaystyle V = \int_0^{2\pi} (1/3) \; d\theta \)
\( = \dfrac{1}{3} \left[ \theta \right]_0^{2\pi} \)
\( = \dfrac{2\pi}{3} \)
예제 2
문제: 이중 적분을 계산하십시오 \( \displaystyle V = \int_0^{1} \int_0^{\sqrt{1-x^2}} e^{x^2+y^2} \; dy \; dx \)
예제 2의 해결책
주어진 적분은 직사각형 좌표에서 쉽게 계산할 수 없으므로 대신 극좌표를 사용하여 쉽게 평가할 수 있습니다.
\( f(x,y) = e^{x^2+y^2} \) 를 극좌표로 표현해 봅시다.
\( r^2 = x^2 + y^2 \)
따라서 극좌표에서의 함수 \( f(x,y) \)는 다음과 같습니다.
\( f(r,\theta) = e^{r^2} \)
직사각형 좌표에서 적분 영역 \( R \)은 주어진 적분 한계에 의해 정의됩니다.
\( R: \) \( 0 \le x \le 1 \) 그리고 \( 0 \le y \le \sqrt{1-x^2} \)
부등식 \( y \le \sqrt{1-x^2} \) 를 그래프로 해결해 봅시다
부등식 양변에 제곱합니다
\( y^2 \le 1-x^2 \)
\( x \)와 \( y \)의 항을 왼쪽에 넣어 다시 작성합니다
\( y^2 + x^2 \le 1 \)
위의 부등식은 원점 \( (0,0) \)을 중심으로 하는 원 내부 또는 원 둘레의 모든 점 \( (x,y) \)을 나타냅니다.
모든 부등식을 합치면, 적분 영역 \( R \)은 아래와 같이 표시됩니다.

극좌표에서의 적분 영역은 아래와 같습니다

위 영역은 다음과 같은 부등식에 의해 정의됩니다
\( R: \) \( 0 \le \theta \le \pi/2 \) 그리고 \( 0 \le r \le 1 \)
적분은 이제 극좌표로 다음과 같이 변환될 수 있습니다
\( \displaystyle V = \int_0^{1} \int_0^{\sqrt{1-x^2}} e^{x^2+y^2} \; dy \; dx = \int_0^{\pi/2} \int_0^1 e^{r^2} r \; dr \; d\theta \)
내부 적분 \(I \)를 다음과 같이 정의합시다
\( \displaystyle I = \int_0^1 e^{r^2} r \; dr \)
평가합니다
\( \displaystyle I = \left[ \dfrac{1}{2} e{r^2} \right]_0^1 \)
\( = \dfrac{1}{2} (e - 1) \)
\( I \)를 적분 \( V \)에 대입합니다
\( \displaystyle V = \int_0^{\pi/2} \dfrac{1}{2} (e - 1) \; d\theta \)
\( = \dfrac{\pi}{4} (e - 1) \)
예제 3
문제: \( \displaystyle V = \iint_R {x^2+y^2} \; dy \; dx \) 을 표현하십시오. 여기서 \( R \)은 \( xy \) 평면에서 점 \( (1,0) \)을 중심으로 하는 반지름이 \( 1 \)인 원이며, 직교 (또는 직사각형) 및 극좌표를 사용하여 적분을 계산하십시오? 적분을 계산하십시오.
예제 3의 해결책
먼저 적분 영역 \( R \)을 그래프로 작성하고 직사각형 및 극좌표로 정의합니다.
1) 직사각형 좌표
원점 \( (1,0) \)을 중심으로 하고 반지름이 \( 1 \)인 원의 방정식은 다음과 같습니다
\( (x-1)^2 + y^2 = 1 \)
확장하여 항을 그룹화합니다
\( x^2 - 2x + y^2 = 0 \)
위의 방정식을 \( y \)에 대해 해결하여 두 해를 얻습니다
\( y = \pm \sqrt {2x-x^2} \)
수직으로 분할하는 경우, 영역 \( R \)은 다음과 같은 부등식으로 설명됩니다
\( R: \) \( 0 \le x \le 2 \) 그리고 \( - \sqrt {2x-x^2} \le y \le \sqrt {2x-x^2} \)
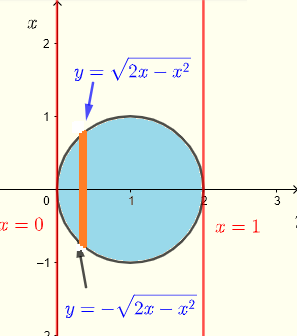
적분은 다음과 같이 쓸 수 있습니다
\( \displaystyle V = \int_0^2 \int_{-\sqrt {2x-x^2}}^{\sqrt {2x-x^2}} \; \; (x^2+y^2) \; dy \; dx \)
내부 적분 \( I_1 \)을 다음과 같이 정의합시다
\( \displaystyle I_1 = \int_{-\sqrt {2x-x^2}}^{\sqrt {2x-x^2}} \; \; (x^2+y^2) \; dy \)
평가 \( I_1 \)
\( \displaystyle I_1 = 2x^2\sqrt{2x-x^2}+2\cdot \frac{\left(2x-x^2\right)^{\frac{3}{2}}}{3} \)
다음 단계는 직사각형 좌표에서 위의 적분을 계산하는 것입니다.
2) 극좌표
원점에서 원 위의 점까지의 선분을 사용하여: 원점에서 \( r = 0 \); 원 위의 점에서 \( r = \sqrt {x^2 + y^2} \)
원의 방정식을 극좌표 형식으로 변환합시다. \( x^2 + y^2 = 2x \)
직교좌표와 극좌표 간의 관계에 따라 [6], 다음과 같이 얻을 수 있습니다
\( r^2 = x^2 + y^2 \) 그리고 \( x = r \cos \theta \)
\( x^2 + y^2 \) 대신 \( r^2 \) 및 \( x \) 대신 \( r \cos \theta \)을 방정식 \( x^2 + y^2 = 2x \)에 대입하여
\( r^2 = 2 r \cos \theta \)
위의 방정식 양변을 \( r \)로 나눕니다
\( r = 2 \cos \theta \)
극좌표에서, 적분 영역 \( R \)은 다음과 같은 부등식으로 설명됩니다
\( R: \) \( -\pi/2 \le \theta \le \pi/2 \) 그리고 \( 0 \le r \le 2 \cos \theta \)

\( r^2 = x^2 + y^2 \)를 사용하여
적분을 극좌표 형태로 쓸 수 있습니다
\( \displaystyle V = \int_{-\pi/2}^{\pi/2} \int_{0}^{2 \cos \theta} r^2 \; r \; dr \; d\theta \)
내부 적분 \(I \)을 다음과 같이 정의합시다
\( \displaystyle I = \int_{0}^{2 \cos \theta} r^2 \; r \; dr \)
평가합니다
\( \displaystyle I = \left[ r^4 / 4 \right]_{0}^{2 \cos \theta} \)
\( \displaystyle I = 4 cos^4 \theta \) (식 1)
위의 표현식 \( \cos^4 \theta \)의 지수를 줄입니다
\( \cos^4 \theta = \cos^2 \theta \cos^2 \theta \)
지수를 줄이는 정체를 사용합니다
\( \cos^2 \theta = \dfrac{cos (2\theta) + 1}{2} \)
따라서
\( \cos^4 \theta = \left( \dfrac{\cos (2\theta) + 1}{2} \right)^2 \)
\( = \dfrac{\cos^2(2\theta) + 2 \cos (2\theta) + 1}{4} \)
한 번 더 지수를 줄이기 위해 정체를 사용하여
\( \cos^4 \theta = \dfrac{\cos(4\theta) + 4\cos(2\theta) }{8} + 3/8 \)
이제 (식 1)에 위의 표현식을 대입하여
\( I = \dfrac{\cos(4\theta) + 4\cos(2\theta) }{2} + 3/2 \)
적분에 \( I \)를 대입하고 평가합니다
\( \displaystyle V = \int_{-\pi/2}^{\pi/2} (\dfrac{\cos(4\theta) + 4\cos(2\theta) }{2} + 3/2 ) \; d\theta \)
\( \displaystyle = \left[ \frac{1}{2}\left(\frac{1}{4}\sin \left(4\theta\right)+2\sin \left(2\theta\right)\right)+\frac{3}{2}\theta \right]_{-\pi/2}^{\pi/2} \)
\( = \dfrac{3\pi}{2} \)
주어진 적분은 극좌표를 사용하여 훨씬 쉽게 평가됩니다.
예제 4
문제: 적분을 극좌표로 변환하고 평가하십시오.
\( \displaystyle V = \int_{-1}^0 \int_{-\sqrt{1-x^2}}^0 \dfrac{\sqrt{x^2+y^2}}{1+\sqrt{x^2+y^2}} \; dy \; dx \)
예제 4의 해결
직사각형 좌표에서 적분의 한계에서 우리는 적분 영역 \( R \)을 추론할 수 있습니다. 이는 III사분면에 있는 원의 1/4입니다.
\( R: \) \( 0 \le x \le 2 \) 그리고 \( - \sqrt {1-x^2} \le y \le 0 \)
그리고 아래 그래프로 나타냅니다
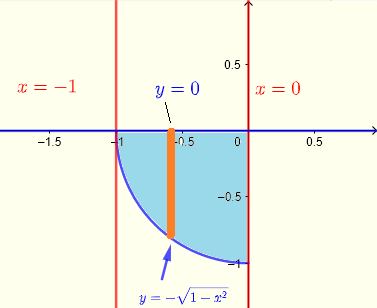
극좌표를 사용하여 적분 영역을 다음과 같이 정의할 수 있습니다.
\( R: \) \( \pi \le \theta \le 3\pi/2 \) 그리고 \( 0 \le r \le 1 \)
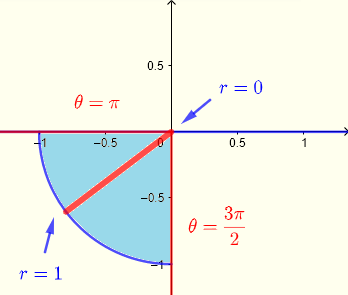
주어진 적분을 극좌표 형식으로 쓰려면 \( r = \sqrt { x^2 + y^2 } \)를 사용합니다
\( \displaystyle V = \int_{\pi}^{3\pi/2} \int_{0}^{1} \dfrac{r}{1+r} \; r \; dr \; d\theta \)
\( \displaystyle = \int_{\pi}^{3\pi/2} \int_{0}^{1} \dfrac{r^2}{1+r} \; dr \; d\theta \)
적분식 \( \dfrac{r^2}{1+r} \)을 다음과 같이 확장합니다
\( \dfrac{r^2}{1+r} = r-1+\frac{1}{r+1} \)
확장된 적분식을 적분에 대입합니다
\( \displaystyle V = \int_{\pi}^{3\pi/2} \int_{0}^{1} (r-1+\frac{1}{r+1}) \; dr \; d\theta \)
적분합니다
\( \displaystyle = \int_{\pi}^{3\pi/2} \left[ \dfrac{r^2}{2} - r + ln |r+1| \right]_0^1 d\theta \)
평가합니다
\( \displaystyle = \int_{\pi}^{3\pi/2} (\ln (2)-\dfrac{1}{2}) d\theta \)
적분합니다
\( = \left( \ln (2)-\dfrac{1}{2} \right) \left[ \; \theta \; \right]_{\pi}^{3\pi/2} \)
평가합니다
\( V = \dfrac{\pi}{2} \left( \ln (2)-\dfrac{1}{2} \right) \)
추가 문제와 답변
Part 1
각 적분을 극좌표로 변환하고 평가하십시오.
-
\( \displaystyle V = \int_{-1}^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \; \; \sin(x^2+y^2) \;dy \;dx \)
-
\( \displaystyle V = \int _0^2\:\:\int _0^{\sqrt{4-x^2}} \sqrt{x^2+y^2} \:\;dy\:\;dx\: \)
Part 2
-
\( \displaystyle V = \iint_R \: e^{\sqrt{x^2+y^2}} \; dx \; dy \)를 평가하십시오. 여기서 \( R \)은 아래 다이어그램에 표시된 영역(파란색)입니다.
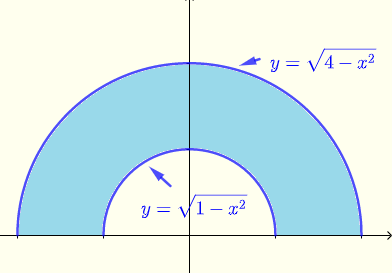
위의 문제에 대한 답변
Part 1:
-
직사각형 좌표에서 적분의 한계에서 주어진 적분 영역의 정의 및 극좌표(오른쪽)는 아래와 같습니다.

\( \displaystyle V = \int_{-1}^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \; \; \sin(x^2+y^2) \;dy \;dx \)
위의 적분을 극좌표로 변환합니다.
\( \displaystyle V = \int_{0}^{2\pi} \int_0^1 \; \; \sin(r^2) \;r \; dr \;d\theta \)
평가합니다
\( = \pi (1 -\cos 1) \)
-
직사각형 좌표에서 적분의 한계에서 주어진 적분 영역의 정의 및 극좌표(오른쪽)는 아래와 같습니다.
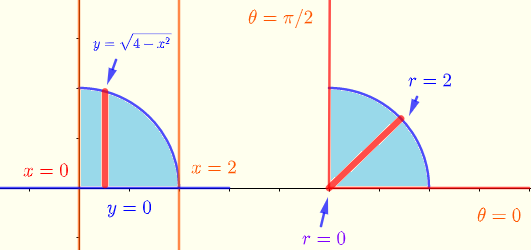
\( \displaystyle V = \int _0^2\:\:\int _0^{\sqrt{4-x^2}} \sqrt{x^2+y^2} \:\;dy\:\;dx\: \)
위의 적분을 극좌표로 변환합니다.
\( \displaystyle V = \int_{0}^{\pi/2} \int_0^2 \; \; r^2 \; dr \;d\theta \)
평가합니다
\( = \dfrac{4\pi }{3} \)
Part 2
직사각형 좌표를 사용하여 주어진 적분을 평가합니다.
\( \displaystyle V = \int_{-2}^{2} \int_0^{\sqrt{4-x^2}} \: e^{\sqrt{x^2+y^2}} \; dy \; dx - \int_{-1}^{1} \int_0^{\sqrt{1-x^2}} \: e^{\sqrt{x^2+y^2}} \; dy \; dx \)
이는 기본 함수를 사용하여 매우 어렵습니다.
극좌표에서의 적분 영역은 아래와 같습니다.
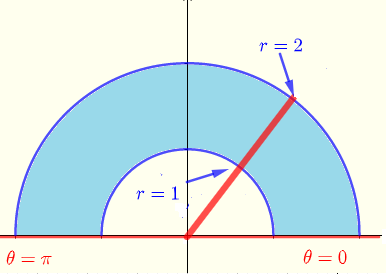
\( R: \) \( 0 \le \theta \le \pi \) 그리고 \( 1 \le r \le 2 \)
주어진 적분식은 극좌표에서 다음과 같습니다.
\( \displaystyle V = \int_0^{\pi} \; \int_1^2 \: r e^{r} \; dr \; d\theta \)
평가합니다
\( = \pi e^2 \)
추가 참고 자료 및 링크
- Joel Hass, University of California, Davis; Maurice D. Weir Naval Postgraduate School; George B. Thomas, Jr.Massachusetts Institute of Technology ; University Calculus , Early Transcendentals, Third Edition
, Boston Columbus , 2016, Pearson.
- Double Integrals Calculations
Double integrals over general regions
- Howard Anton, Irl C. Bivens, Stephen Davis ; Calculus: Early Transcendentals; Willey, 2012.
- Gilbert Strang; MIT, Calculus, Wellesley-Cambridge Press, 1991
- polar coordinates
- Convert Polar to Rectangular Coordinates and Vice Versa
Engineering Mathematics with Examples and Solutions
-example-1.gif)