펄스 \( f(t) \)와 그 푸리에 변환 \( F(\omega) \)을 시각화하는 상호작용 온라인 그래핑 계산기입니다. \( t \)는 시간이고 \( \omega \)는 각주파수입니다.
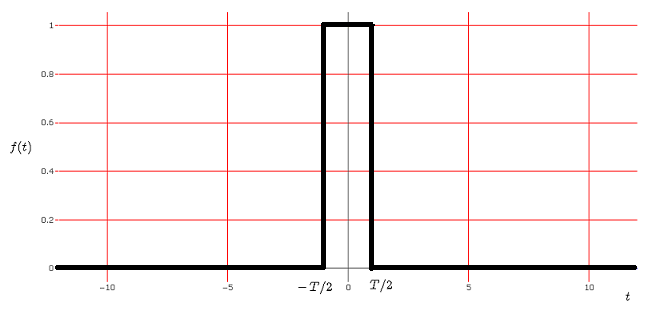\( f(t) \)의 푸리에 변환은 다음과 같이 정의됩니다.
\[ F(\omega) = \int_{-\infty}^{+\infty} f(t) e^\left( - j \omega t\right) dt \\
= \int_{-T/2}^{+T/2} 1 \cdot e^\left( - j \omega t\right) dt \\
= \left[ \dfrac{ e^\left( - j \omega t \right)}{-j \omega} \right]^{T/2}_{-T/2}
\]
계산하고 단순화하여 얻은 결과는 다음과 같습니다.
\[ F(\omega) = \dfrac{\sin(\omega(T/2))}{\omega/2}
\]
T =