시리즈 RLC 회로에서 전류와 전압 계산

목차

복소 임피던스를 사용하여 시리즈 RLC 회로에서 전류와 전압을 분석하는 방법에 대해 논의되어 있습니다. 복소수는 교류 회로에서 임피던스, 전류 및 전압의 계산을 크게 단순화합니다. 교류 회로에서 전류에는 기호 \( i \)가 사용되므로 여기서는 \( j \)를 \( j^2 = -1 \) 또는 \( j = \sqrt{-1} \)로 정의된 허수 단위로 사용합니다. 전류와 전압의 소문자는 실수 양에 사용되고, 대문자는 편극 형태의 복소수에 사용됩니다.

A - 복소수로서의 임피던스 및 시리즈 RLC 회로의 페이저

주파수 \( f \)의 전압원에 의해 공급되는 회로의 경우, 다른 RLC 구성 요소의 임피던스는 다음과 같습니다:
복소형으로 된 저항 \( R \)의 임피던스 \( Z_R \)는 다음과 같습니다. \[ Z_R = R \] 복소형으로 된 인덕터 \( L \)의 임피던스 \( Z_L \)(인덕티브 리액턴스라고도 함)는 다음과 같습니다. \[ Z_L = j \omega L \] 복소형으로 된 캐패시터 \( C \)의 임피던스 \( Z_C \)(용량 리액턴스라고도 함)는 다음과 같습니다. \[ Z_C = - \dfrac{1}{\omega C} j \] 여기서 \( \omega = 2 \pi f \)
주목해야 할 가장 중요한 점은 유도성 및 용량성 리액턴스가 전압원의 주파수에 따라 달라진다는 것입니다.

\( V_i \), \( I \), \( V_R \), \( V_L \) 및 \( V_C \)를 각각 \( v_i \), \( i \), \( v_R \), \( v_L \) 및 \( v_C \)의 복소형이라고 합시다.
복소 임피던스로 확장된 키르호프 전압 법칙을 적용하여 다음을 쓰세요.
\( V_i - V_R - V_L - V_C = 0 \)     (1)
복소 임피던스로 확장된 오옴의 법칙을 적용하여 다음을 쓰세요.
\( V_R = Z_R I \)
\( V_L = Z_L I \)
\( V_C = Z_C I \)
위의 식을 식 (1)에 대입하여 다음을 얻습니다.
\( V_i = Z_R I + Z_L I + Z_C I = 0 \)
위의 식을 \( I \)에 대해 해결합니다.
\( I = \dfrac{V_i}{Z_R + Z_L + Z_C} \)
시리즈 RLC 회로의 동등한 복소 임피던스 \( Z \)를 다음으로 정의합시다.
\[ Z = Z_R + Z_L + Z_C = R + j \left(\omega L - \dfrac{1}{\omega C} \right) \]
\( Z \)의 모듈러스: \[ |Z| = \sqrt{R^2 + \left(\omega L - \dfrac{1}{\omega C}\right)^2} \]
\( Z \)의 인자: \[ \theta = arctan \left( \dfrac {\omega L - \dfrac{1}{\omega C}}{R} \right) \]
임피던스 \( Z \)의 모듈러스와 인자가 모두 소스 전압의 주파수 (\( \omega = 2 \pi f \))에 의존한다는 점을 유의하십시오. 이 특성은 필터 설계에 유용하며 전자 회로의 여러 응용 프로그램이 있습니다.
\( Z \)를 극 좌표 형태로 씁니다. \[ Z = |Z| \; \angle \; \theta \]
위에서 수행한 \( Z_R, Z_L, Z_C \) 및 \( Z \)의 표현은 아래에 표시된 페이저를 사용하여 기하학적으로 해석될 수 있습니다.


(a)에서 \( Z_R, Z_L\) 및 \( Z_C \)는 수평 축을 따라 실수 부분을, 수직 축을 따라 허수 부분을 가지고 있는 좌표계에 표시됩니다.
(b)에서 \( Z = Z_R + Z_L + Z_C \)가 벡터(또는 복소수) 추가를 사용하여 기하학적으로 표시됩니다.
(c)에서 \( Z \)의 절대값을 나타내는 삼각형이 그려집니다. 피타고라스 정리를 사용하여 \( |Z| = \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C}\right)^2} \)로 정확히 복소수를 사용하여 얻은 것과 동일합니다.
다시 말해서 삼각형을 사용하여 각도 : \( \theta = \arctan \left (\dfrac{\omega L - \dfrac{1}{\omega C}}{R} \right) \)

B - 시리즈 RLC 회로의 전류와 전압

\( v_i = V_0 \cos ( \omega t) \) , 여기서 \( V_0 \)는 전원 전압의 최대치입니다.
복소수의 Euler 공식
\( e^{j \omega t} = \cos (\omega t) + j \sin (\omega t )\)
따라서 \( v_i \)는 다음과 같이 쓸 수 있습니다.
\( v_i \) 는 \( e^{j \omega t} \)의 실수 부분과 같습니다.
우리는 이제 "실수 부분의"을 제거하고 모든 계산을 복소수로 수행하고 복소수 형태의 \( V_i \)를 다음과 같이 정의합니다.
\( V_i = V_0 e^{j \omega t} \)
그리고 복소수 형태로 \( I \)를 유도합니다.
\( I = \frac{V_0 e^{j\omega t}}{|Z| \; \angle \; \theta} \)
극 형태로 나타낸 \( I \)는 다음과 같습니다.
\( I = \dfrac{V_0}{|Z|} \; \angle \; \omega t - \theta \)
\( I = I_0 \; \angle \; \omega t - \theta \) , 여기서 \( I_0 = \dfrac{V_0}{|Z|} \)
임피던스 \( Z_R, Z_L\) 및 \( Z_C \)를 극 형태로 다시 씁니다.
\( Z_R = R = R \; \angle \; 0 \)
\( Z_L = j \omega L = \omega L \; \angle \; \pi/2\)
\( Z_C = - \dfrac{1}{\omega C} j = \dfrac{1}{\omega C} \; \angle \; - \pi/2\ \)
전압은 다음과 같습니다.
\( V_R = Z_R I = (R \; \angle \; 0) (I_0 \; \angle \; {\omega t - \theta}) = R I_0 \angle \; \omega t - \theta \)
\( V_L = Z_L I = (\omega L \; \angle \; \pi/2) (I_0 \; \angle \; {j\omega t - \theta}) = \omega L I_0 \; \angle \; {\omega t - \theta + \pi/2} \)
\( V_C = Z_C I = (\dfrac{1}{\omega C} \; \angle \; - \pi/2) (I_0 \; \angle \; {j\omega t - \theta}) = \dfrac{I_0}{\omega C} \; \angle \; {\omega t - \theta - \pi/2} \)
전류 \( I \) 및 전압 \( V_R \) , \( V_C \) 및 \( V_C \)는 아래의 페이저를 사용하여 표시됩니다.

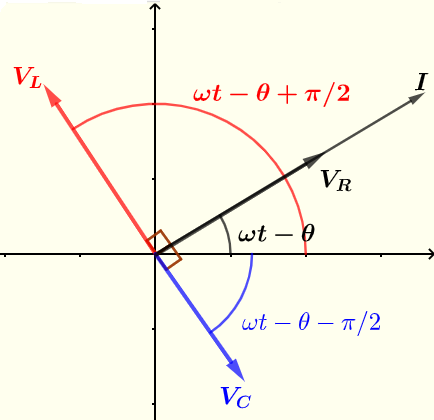
복소 (또는 극형) 형태의 전류와 전압의 실수 부분은 위에서 얻은 복소수의 실수 부분입니다.
\( i = \dfrac{V_0}{|Z|} \cos( \omega t - \theta) \)

\( v_R = R \dfrac{V_0}{|Z|} \cos(\omega t - \theta) \)

\( v_L = \omega L \dfrac{V_0}{|Z|} \cos(\omega t - \theta + \pi/2) \)

\( v_C = \dfrac{V_0}{\omega C|Z|} \cos(\omega t - \theta - \pi/2) \)

참고 : 시간 변화 \( \omega t \)는 계산 중에 무시할 수 있으며, 시간의 함수로 전류와 전압을 작성해야 할 경우 나중에 추가할 수 있습니다. 아래의 예시는 시간 의존성을 무시하고 RLC 회로를 분석하는 방법을 보여줍니다.

C - 상세한 해와 함께하는 예시

예시 1
시리즈 RLC 회로에서 전원 전압은 \( v_i = 20 \cos (\omega t) \)으로 주어지며, \( \omega = 1000 \; rad/s \)일 때, 캐패시터의 용량 \( C = 200 \; \mu F \), 인덕터의 인덕턴스 \( L = 400 \; mH\) 및 저항의 저항 \( R = 400 \; \Omega \)입니다.
a) 캐패시터, 인덕터 및 저항의 임피던스 및 복소 형태로 RLC 회로의 등가 임피던스 \( Z \)를 찾습니다.
b) 복소 형태로 전류 및 모든 전압을 찾습니다.
c) 실제 전류 및 전압을 찾습니다.

예시 1의 해결책
a)
저항 \( R \)의 복소 형태의 임피던스 \( Z_R \)는 다음과 같습니다.
\( Z_R = R = 400 \; \Omega \)
인덕터 \( L \)의 복소 형태의 임피던스 \( Z_L \)는 다음과 같습니다.
\( Z_L = j \omega L = j \cdot 1000 \cdot 400 \cdot 10^{-3} = 400 j \; \Omega \)
캐패시터 \( C \)의 복소 형태의 임피던스 \( Z_C \)는 다음과 같습니다.
\( Z_C = - \dfrac{1}{\omega C} j = - \dfrac{1}{1000 \cdot 200 \cdot 10^-6} j = - 5 j \; \Omega \)
\( Z = Z_R + Z_L + Z_C = 400 + 400 j - 5 j = 400 + 395 j \)
b)
\( v_i = 20 \cos ( \omega t) \), 따라서 전원 전압의 극 형태는 다음과 같습니다. \( V_i = 20 \; \angle \; 0\)
위에서 본 바와 같이 전류의 극 형태는 다음과 같습니다.
\( I = \dfrac{V_i}{Z_R + Z_L + Z_C } \)
알려진 값으로 대체합니다.
\( I = \dfrac{20 \; \angle \; 0}{400 + 395 j}\)
분모를 극 형태로 다시 씁니다.
\( 400 + 395 j = \sqrt {400^2+395^2} \; \angle \; \arctan\left(\dfrac{395}{400}\right) = 562.16 \; \angle \; 44.64^{\circ} \)
\( I \)를 평가합니다.
\( I = \dfrac{20 \; \angle \; 0}{562.16 \; \angle \; 44.64^{\circ}} = \dfrac{20}{562.16} \; \angle \; 0 - 44.64^{\circ} \)
간단히 합니다.
\( I = 0.0356 \; \; \angle \; - 44.64^{\circ} \) A
\( V_R = R I = 400 (0.0356 \; \; \angle \; - 44.64^{\circ}) = 14.24 \; V \; \angle \; - 44.64^{\circ}\) V
\( V_L = Z_L I = 400 j (0.0356 \; \; \angle \; - 44.64^{\circ}) = 14.24 \; V \; \angle \; 45.36^{\circ}\) V
\( V_C = Z_C I = - 5 j (0.0356 \; \; \angle \; - 44.64^{\circ}) = 0.18 \; V \; \angle \; -134.6^{\circ}\) V

예시 2
시리즈 RLC 회로에서 전원 전압은 \( v_i = 10 \cos (\omega t) \)으로 주어지며, 캐패시터의 용량 \( C = 200 \; \mu F \), 인덕터의 인덕턴스 \( L = 200 \; mH\) 및 저항의 저항 \( R = 500 \; \Omega \)입니다.
a) 임피던스 \( Z \)의 허수 부분이 0과 같아지는 각주 \( \omega \)를 찾습니다.
b) 부분 a에서 찾은 주파수에 대해 전류와 전압을 찾습니다.

예시 2의 해결책
a)
시리즈 RLC 회로에서 \( Z = R + j(\omega L - \dfrac{1}{\omega C} ) \)
\( Z \)의 허수는 다음과 같습니다.
\( \omega L - \dfrac{1}{\omega C} = 0 \)
\( \omega \)에 대해 풀어서
\( \omega^2 L C = 1 \)
\( \omega = \dfrac{1}{\sqrt{L C}} \)
\( L \)과 \( C \)에 그들의 수치 값을 대입합니다.
\( \omega = \dfrac{1}{ \sqrt{ 200\cdot10^{-3} \cdot 200 \cdot 10^{-6}}} = 158.11 \) rad/s
b)
\( I = \dfrac{V_i}{Z} = \dfrac{10 \; \angle \; 0}{R \; \angle \; 0} = \dfrac{10}{500} \; \angle \; 0 = 0.02 \; \angle\; 0 \)
\( V_R = R I = 500 \cdot 0.02 \; \angle \; 0 = 10 \; \angle\; 0 \)
\( V_C = Z_C I = \dfrac{1}{\omega C} \; \angle \; -90^{\circ} \cdot 0.02 \; \angle\; 0 = \dfrac{1}{\omega C} \cdot 0.02 \; \angle \; -90^{\circ} = \dfrac{1}{158.11 \cdot 200 \cdot 10^{-6}} \cdot 0.02 \; \angle \; -90^{\circ} = 0.6324 \; \angle \; -90^{\circ} \)
\( V_L = Z_L I = \omega L \; \angle \; 90^{\circ} \cdot 0.02 \; \angle\; 0 = \omega L \cdot 0.02 \; \angle \; 90^{\circ} = 158.11 \cdot 200 10^{-3} \cdot 0.02 \; \angle \; 90^{\circ} = 0.6324 \; \angle \; 90^{\circ} \)

예시 3
시리즈 RLC 회로에서 전원 전압은 \( v_i = V_0 \cos (2 \pi f t) \)로 주어지며, 여기서 \( f \)는 주파수이며, 캐패시터의 용량은 \( C = 47 \; \mu F \), 인덕터의 인덕턴스는 \( L = 100 \; mH\), 그리고 저항의 저항은 \( R = 200 \; \Omega \)입니다.
a) 주파수 \( f \)에 따른 캐패시터, 인덕터 및 저항의 시리즈와 동등한 총 임피던스 \( Z \)를 찾아 극 형태로 기록하십시오 \( Z = |Z| \; \angle \; \theta \)
b) \( \theta = -60^{\circ} \)인 주파수 \( f \)를 찾으십시오.

예시 3의 해결책
a)
시리즈 RLC 회로에서 \( Z = R + j(\omega L - \dfrac{1}{\omega C}) \)
알려진 수량을 그들의 수치 값으로 대체합니다
\( Z = R + j(\omega L - \dfrac{1}{\omega C}) = 200 + j( \omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}})\)
\( Z = \sqrt {200^2 + ( \omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}})^2} \; \angle \; \arctan \left(\dfrac{\omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}}}{200}\right) \)
b)
\( \arctan \left(\dfrac{\omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}}}{200}\right) = -60^{\circ} \)
\( \dfrac{\omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}}}{200} = \tan (-60^{\circ}) = -1.73205 \)
방정식의 모든 항을 \( 200 \)으로 곱하여 분모를 제거하십시오
\( \omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}} = -346.41 \)
방정식의 모든 항을 \( \omega \cdot 47 \cdot 10^{-6} \)으로 곱하여 분모를 제거하십시오
\( 47 \cdot 10^{-7} \omega^2 - 1 = -0.01628127 \omega \)
위의 이차 방정식을 \( \omega \)에 대해 풀고 양의 해를 선택하십시오.
\( \omega = 53.23 \) rad/s
\( \omega = 2 \pi f = 60.3682 \)
\( f = \dfrac{60.3682}{2 \pi} = 9.60789 \) Hz

예시 4
시리즈 RLC 회로에서 전원 전압은 \( v_i = V_0 \cos (2 \pi f t) \)로 주어지며, 캐패시터의 용량은 \( C = 470 \mu \)F, 인덕터의 인덕턴스는 \( L = 50 \)mH이며, 저항의 저항은 \( R \)입니다.
a) 주파수 \( f \)에 따른 캐패시터, 인덕터 및 저항의 시리즈와 동등한 총 임피던스 \( Z \)를 찾아 극 형태로 기록하십시오 \( Z = |Z| \; \angle \; \theta \)
b) \( \theta = 40^{\circ} \) 및 \( |Z| = 100 \)인 저항 \( R \) 및 주파수 \( f \)를 찾으십시오.

예시 4의 해결책
a)
시리즈 RLC 회로에서 \( Z = R + j(\omega L - \dfrac{1}{\omega C}) \)
\( Z \)를 극 형태로 씁니다
\( Z = \sqrt{R^2 + (\omega L - \dfrac{1}{\omega C})^2} \; \angle \; \arctan \left( \dfrac{\omega L - \dfrac{1}{\omega C}}{R} \right) \)
b)
\( \theta = \arctan \left( \dfrac{\omega L - \dfrac{1}{\omega C}}{R} \right) = 40^{\circ} \)
\( \dfrac{\omega L - \dfrac{1}{\omega C}}{R} = \tan 40^{\circ} = 0.83909\)
\( \omega L - \dfrac{1}{\omega C} = 0.83909 R \)
위의 값을 \( |Z| \)에 대입하십시오
\( \sqrt{R^2 + (0.83909 R)^2} = 100 \)
\( R \)을 풀어보십시오
\( R = 76.6048 \; \Omega \)
\( \omega L - \dfrac{1}{\omega C} = 0.83909 R = 64.27832 \)
\( \omega \)를 풀어보십시오
\( \omega = 1317.8557 \) rad/s
\( f = \dfrac{1317.8557}{2\pi} = 209.74324 \) Hz

더 많은 참고 자료 및 링크