복소수를 사용하여 교류 회로

목차

복소수를 사용하여 교류(교대 전류) 회로에서 전류 및 전압을 분석하고 계산하는 방법 및 저항의 임피던스, 캐패시터의 임피던스 및 인덕터의 임피던스가 복소수로 표현되는 방법을 수학적으로 설명합니다. 또한 복소 임피던스의 사용으로 Ohm의 법칙과 유사한 법칙을 사용하여 교류 회로를 수학적으로 모델링하는 방법도 보여줍니다.
복소수를 사용하여 교류 회로 및 여러 분야의 사인파 현상을 모델링하는 데 적합한 두 가지 주요 이유는 다음과 같습니다.
1) 교류 신호(및 여러 사인파 현상)는 복소수의 크기 및 위상과 매우 유사하며, 각각 복소수의 절대값 및 인수입니다.
2) 복소수의 기본 연산(덧셈, 뺄셈, 곱셈 및 나눗셈)은 컴퓨터에서 수행 및 프로그래밍하기가 더 쉽습니다.
참고
1) AC 회로에서 전류를 나타내는 기호로 \( i \)를 사용하므로, 여기서는 \( j \)를 \( j^2 = -1 \) 또는 \( j = \sqrt{-1} \)로 정의된 허수 단위로 사용합니다.
2) 기호 \( \Re e\)는 복소수의 실수 부분을 나타냅니다.

A - 복소수의 실수 부분

표준형의 복소수 \( Z = a + j b \) 지수 형식으로 다음과 같이 작성할 수 있습니다.
\( \displaystyle Z = r e^{j \theta} \)      여기서 \( j^2 = -1 \)
및 극 좌표 형식으로 다음과 같이 작성할 수 있습니다.
\( Z = r \angle \theta \)
여기서 \( r = \sqrt{a^2 +b^2} \)는 \( Z \)의 절대값이고, \( \tan \theta = \dfrac{b}{a} \)는 \( Z \)의 인수입니다.
복소수의 지수 형식의 양변의 실수 부분을 따로 작성합니다.
\( \Re e (r e^{j \theta}) = \Re e (r ( \cos \theta + j \sin \theta )) = \Re e (r \cos \theta + j r \sin \theta ) = r \cos \theta \)
이후에는 \( \Re e \)는 주어진 복소수의 실수 부분을 의미합니다.

B - 단일 변수를 가진 복소 함수의 도함수

\( f(t) \)를 변수 \( t \)를 가진 복소 함수로 하여 다음과 같이 작성하십시오.
\( f(t) = a(t) + j b(t) \)
여기서 \( a(t) \)는 \( f(t) \)의 실수 부분이고, \( b(t) \)는 \( f(t) \)의 허수 부분이며, \( j = \sqrt {-1}\)는 허수 단위입니다.
\( f'(t) \)를 \( t \)에 대한 \( f(t) \)의 첫 번째 도함수로 정의합니다.
\( f'(t) = \lim_{h\to 0} \dfrac{f(t+h) - f(t) }{h} \)
위의 공식에서 \( f(t+h) \)를 \( a(t+h) + j b(t+h) \)로 대체합니다.
\( f'(t) = \lim_{h\to 0} \dfrac{ a(t+h) + j b(t+h) - (a(t) + jb(t))}{h} \)
다음과 같이 항을 분리합니다.
\( f'(t) = \lim_{h\to 0} \dfrac{ a(t+h) - a(t)}{h} + j \lim_{h\to 0} \dfrac{ j b(t+h) - jb(t))}{h} \)
\( f'(t) = a'(t) + j b'(t) \)
이제 \( f(t) \)의 실수 부분의 도함수가 \( f(t) \)의 실수 부분의 도함수와 같음을 보여주는 것이 쉽습니다.
\( \Re e(f'(t)) = a'(t) = (\Re e(f(t))' \)
또는
\( \Re e \left ( \dfrac{df(t)}{dt} \right) = \dfrac {d a(t)}{dt} = \dfrac {d \left (\Re e(f(t)) \right)}{dt} \)

C - 단일 변수를 가진 복소 함수의 정적분

\( f(t) \)를 변수 \( t \)를 가진 복소 함수로 하여 다음과 같이 작성하십시오.
\( f(t) = a(t) + j b(t) \)
여기서 \( a(t) \)는 \( f(t) \)의 실수 부분이고, \( b(t) \)는 \( f(t) \)의 허수 부분이며, \( j = \sqrt {-1}\)는 허수 단위입니다.
\( F(t) \)를 미정적분으로 정의합니다.
\( \displaystyle F(t) = \int f(t) dt = \int (a(t) + j b(t)) dt = \int a(t) dt + j \int b(t) dt \)
\( f(t) \)의 실수 부분의 정적분이 \( f(t) \)의 실수 부분의 정적분과 같음을 보여주는 것이 쉽습니다.
\( \displaystyle \Re e \left( \int f(t) dt \right) = \int a(t) dt = \int \left( \Re e f(t) \right) dt \)

이제 위의 개념을 사용하여 복소수를 사용하여 간단한 AC 회로를 분석합니다.

D - AC 전압 공급원과 복소수

아래에서 \( v(t) \)는 시간 \( t \)에 따라 변하는 AC 전압 공급원으로 주어집니다. 다음과 같습니다.
\( v(t) = V_0 \cos(\omega t) \)
여기서 \( V_0 \)는 최고 전압과 같은 실수이며, \( \omega = 2 \pi f \)도 주파수입니다.
복소수를 사용하면 \( v(t) \)를 다음과 같이 작성할 수도 있습니다.
\( v(t) = V_0 \cos(\omega t) = \Re e ( V_0 \cos(\omega t) + j V_0 \sin(\omega t) ) = \Re e (V_0 e^{j\omega t} ) \)

E - AC 회로의 저항기

아래 그림과 같이 저항기가 있는 간단한 AC 회로를 고려해 봅시다. \( v(t) \)가 다음과 같은 AC 전압 공급원으로 주어집니다.
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \) 여기서 \( V_0 \) 및 \( \omega \)는 실수입니다.


저항기 \( R \)을 통과하는 전류 \( i \)와 저항기 \( R \)을 통한 전압 \( v(t)_R \) 간의 관계는 다음과 같습니다.
\( v(t)_R = R i \)
위의 단일 루프를 사용하여 다음이 성립합니다.
\( v(t) = v(t)_R \)
\( v(t) \)은 \( v(t) = V_0 \cos(\omega t) \)로 주어지고,
따라서
\( v(t)_R = V_0 cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
위의 내용을 결합하여 다음과 같이 작성합니다.
\( R i = \Re e (V_0 e^{j\omega t} ) \)       (I)
\( V_R = V_0 e^{j\omega t} \)로 정의하고 위의 식 (I)을 다음과 같이 다시 작성합니다.
\( R i = \Re e V_R \)
\( R \)이 실수이므로 위의 내용은 다음과 같이 작성할 수 있습니다.
\( i = \Re e \left( \dfrac{V_R }{R} \right) \)
\( Z_R \)을 저항기의 임피던스로 정의하면 다음과 같습니다.
\( Z_R = R \)
\( R \)이 실수이므로 저항기 \( R \)의 임피던스 \( Z_R \)는 실수입니다.
전류 \( i \)는 다음과 같이 작성할 수 있습니다.
\( i = \Re e \left( \dfrac{ V_R } {Z_R} \right) \)
허락하다
\( I = \dfrac{ V_R } {Z_R} \)
위의 내용은 DC (직류) 회로에서 Ohm의 법칙과 유사한 관계를 제공합니다. 복소수 \( I \), \( V_R \) 및 \( R \) 사이의 위의 관계는 계산을 훨씬 쉽게 만듭니다.
이는 복소 임피던스, 전압 및 전류를 사용하여 계산한 다음 최종 답변으로 실수 부분을 취하는 방식으로 계산을 간단화합니다.

F - AC 회로의 캐패시터

아래와 같이 캐패시터가 있는 간단한 AC 회로를 고려해 봅시다. \( v(t) \)가 다음과 같은 AC 전압 공급원으로 주어집니다.
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)

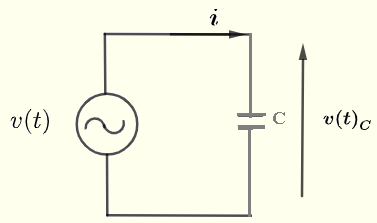
캐패시터 \( C \)를 통과하는 전류 \( i \)와 캐패시터 \( C \)를 통한 전압 \( v(t)_C \) 간의 관계는 다음과 같습니다.
\( \displaystyle v(t)_C = \dfrac{1}{C} \int i dt \)
위의 단일 루프를 사용하여 다음이 성립합니다.
\( v(t) = v(t)_C \)
주어진
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
위의 내용을 모두 결합하여 다음과 같이 작성합니다.
\( \displaystyle \Re e (V_0 e^{j\omega t} ) = \dfrac{1}{C} \int i dt \)
양쪽의 도함수를 취합니다.
\( \displaystyle \dfrac{d}{dt} (\Re e (V_0 e^{j\omega t}) ) = \dfrac{d}{dt} \left(\dfrac{1}{C} \int i dt \right) \)
위의 결과를 B 부분에서 이미 논의한 결과를 사용하여 위의 식을 다시 작성합니다.
\( \displaystyle \Re e \dfrac{d}{dt} \left( V_0 e^{j\omega t} \right) = \dfrac{d}{dt} \left(\dfrac{1}{C} \int i dt \right) \)
간단하게 정리합니다.
\( \Re e \left( j \omega V_0 e^{j\omega t} \right) = \dfrac{1}{C} i \)
캐패시턴스 \( C \)가 실수이므로 다음과 같이 작성할 수 있습니다.
\( i = \Re e \left( j \omega C \; V_0 e^{j\omega t} \right) \)
\( V_C = V_0 e^{j\omega t} \)로 정의하고 캐패시터의 복소 임피던스 \( Z_C \)를 다음과 같이 정의합니다.
\( Z_C = \dfrac{1}{j \omega C} = - \dfrac {j} { \omega C} \)
\( C \)가 실수이므로 캐패시터의 임피던스 \( Z_C \)는 순수 허수입니다.
전류 \( i \)는 다음과 같이 작성할 수 있습니다.
\( i = \Re e \left( \dfrac{ V_C } {Z_C} \right) \)
\( I = \dfrac{ V_C } {Z_C} \)로 정의하면 위의 내용은 다음과 같습니다.
위의 내용은 복소수 \( I \), \( V_C \) 및 \( Z_C \) 사이의 오옴의 법칙과 유사한 관계를 제공합니다.
이는 복소 임피던스, 전압 및 전류를 사용하여 계산한 다음 최종 답변으로 실수 부분을 취하는 방식으로 계산을 간단화합니다.

G - AC 회로의 인덕터

아래와 같이 인덕터가 있는 간단한 AC 회로를 고려해 봅시다. \( v(t) \)가 다음과 같은 AC 전압 공급원으로 주어집니다.
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)

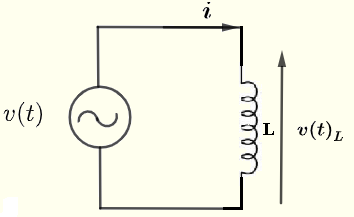
인덕터 \( L \)을 통과하는 전류 \( i \)와 인덕터 \( L \)를 통한 전압 \( v(t)_L \) 간의 관계는 다음과 같습니다.
\( v(t)_L = L \dfrac {d i}{ dt} \)
위의 단일 루프를 사용하여 다음이 성립합니다.
\( v(t) = v(t)_L \)
주어진
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
위의 내용을 모두 결합하여 다음과 같이 작성합니다.
\( \Re e (V_0 e^{j\omega t} ) = L \dfrac {d i}{ dt} \)
양쪽의 미정적분을 취합니다.
\( \displaystyle \int \Re e (V_0 e^{j\omega t}) dt = \int L \dfrac {d i}{ dt} dt \)
위의 결과를 이미 C 부분에서 논의한 결과를 사용하여 다음과 같이 작성합니다.
\( \displaystyle \Re e \int V_0 e^{j\omega t} dt = \int L \dfrac {d i}{ dt} dt \)
양쪽의 적분을 계산합니다.
\( \Re e \left( \dfrac{1}{j\omega} V_0 e^{j\omega t} \right) = L i \)
인덕턴스 \( L \)가 실수이므로 다음과 같이 작성할 수 있습니다.
\( i = \Re e \left( \dfrac{1}{j \omega L} \; V_0 e^{j\omega t} \right) \)
\( V_L = V_0 e^{j\omega t} \)로 정의하고 \( Z_L \)을 다음과 같이 정의합니다.
\( Z_L = j \omega L \)
\( L \)이 실수이므로 캐패시터의 임피던스 \( Z_L \)은 순수 허수입니다.
전류 \( i \)는 다음과 같이 작성할 수 있습니다.
\( i = \Re e \left( \dfrac{ V_L } {Z_L} \right) \)
\( I = \dfrac{ V_L } {Z_L} \)로 정의하면 위의 내용은 다음과 같습니다.
위의 내용은 복소수 \( I \), \( V_L \) 및 \( Z_L \) 사이의 오옴의 법칙과 유사한 관계를 제공합니다.
이는 복소 임피던스, 전압 및 전류를 사용하여 계산한 다음 최종 답변으로 실수 부분을 취하는 방식으로 계산을 간단화합니다.

H - 결론: 복소 임피던스로의 오옴의 법칙

위에서 저항, 캐패시터 및 인덕터의 임피던스를 복소수로 정의할 수 있으며 다음과 같습니다.
1) 저항 \( R\)의 경우; 임피던스는 다음과 같이 주어집니다. \[ Z_R = R \] 그리고 저항 \( R \)을 통한 전류 \( I \) (복소 형태)와 저항 \( R \)을 통한 전압 \( V_R \) (복소 형태) 간의 관계는 AC에서의 오옴의 법칙으로 다음과 같습니다: \[ I = \dfrac{V_R}{Z_R} \] 2) 캐패시터 \( C \)의 경우; 임피던스는 다음과 같이 주어집니다. \[ Z_C = -\dfrac{j}{\omega C} \] 그리고 캐패시터 \( C \)를 통한 전류 \( I \) (복소 형태)와 캐패시터 \( C \)를 통한 전압 \( V_C \) (복소 형태) 간의 관계는 AC에서의 오옴의 법칙으로 다음과 같습니다: \[ I = \dfrac{V_C}{Z_C} \] 3) 인덕터 \( L \)의 경우; 임피던스는 다음과 같이 주어집니다. \[ Z_L = j \omega L \] 그리고 인덕터 \( L \)을 통한 전류 \( I \) (복소 형태)와 인덕터 \( L \)을 통한 전압 \( V_L \) (복소 형태) 간의 관계는 AC에서의 오옴의 법칙으로 다음과 같습니다: \[ I = \dfrac{V_C}{Z_L} \] 우리는 저항, 캐패시터 및 인덕터의 임피던스를 모델링하기 위해 복소수를 사용할 때 AC 회로에서 오옴의 법칙이 성립한다는 것을 알 수 있습니다.
또한 키르흐호프의 법칙도 저항, 캐패시터 및 인덕터의 임피던스를 모델링하기 위해 복소수를 사용할 때 AC 회로에서 성립합니다.
직렬 및 병렬 임피던스에 대한 등가 임피던스는 직렬 및 병렬 저항에 대한 유사한 규칙을 사용하여 계산할 수 있습니다.

E - 해결 예제

예제 1
저항 \( R \)을 통한 전류 \( i \), 저항 \( R \)을 통한 전압 \( v(t)_R \) 및 인덕터 \( L \)을 통한 전압 \( v(t)_L \)을 \( V_0 \), \( R \), \( L \) 및 \( \omega \)의 함수로 찾으세요.
주어진
전압 공급원: \( v(t) = V_0 \cos(\omega t) \), \( \omega = 2 \pi f \), 여기서 \( f \)는 주파수입니다.

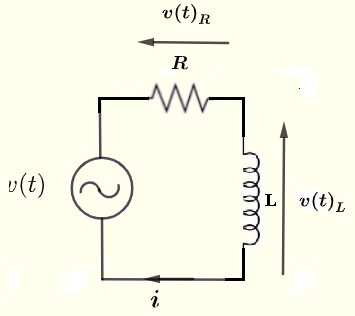
예제 1의 해결
\( v(t) \)의 복소수 형태를 \( V \)로 정의하겠습니다.
저항 \( R \)을 통한 전압 \( v(t)_R \)의 복소수 형태를 \( V_R \)로 정의하겠습니다.
인덕터 \( L \)을 통한 전압 \( v(t)_L \)의 복소수 형태를 \( V_L \)로 정의하겠습니다.
주어진 회로의 저항과 캐패시터를 통한 전류 \( i \)의 복소수 형태를 \( I \)로 정의하겠습니다.
저항의 복소 임피던스를 \( Z_R = R \), 인덕터의 복소 임피던스를 \( Z_L = j \omega L \)로 하겠습니다(위의 H부 참조).
위의 복소수가 정의된 회로를 다시 그리고, 오옴의 법칙과 키르흐호프의 법칙을 적용할 수 있습니다.

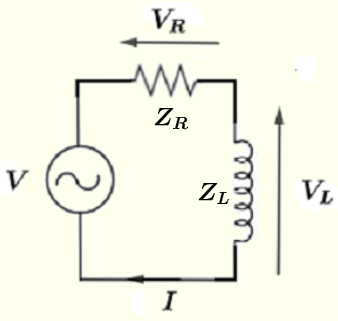
회로를 만드는 루프에서 키르흐호프의 법칙을 사용하면
\( V = V_R + V_L \)         (I)
\( V_R \)과 \( V_L \)을 다시 쓰기 위해 오옴의 법칙을 사용하여
\( V_R = Z_R I \)
\( V_L = Z_L I \)
식 (I)에 대입하면
\( V = Z_R I + Z_L I = R I + j \omega L I = I(R + j \omega L ) \)
위의 식을 \( I \)에 대해 풀면
\( I = \dfrac{V}{R+j \omega L} \)         (II)
분모 \( R+j \omega L \)는 복소수로서 다음과 같이 복소수 형태로 쓸 수 있습니다.
\( R+j \omega L = r e^{j\theta} \)
여기서
\( r = |Z| = \sqrt {R^2 + (L\omega)^2} \)은 절댓값이고
\( \theta = \arctan \left(\dfrac{\omega L}{R} \right) \)은 아래의 복소 평면에 표시된 것처럼 인수입니다.

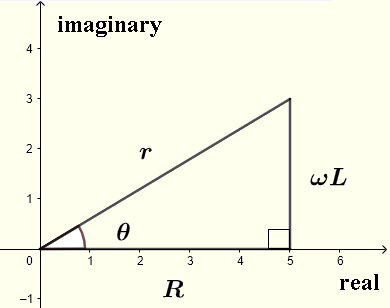
\( V = V_0 e^{j\omega t} \)라고 가정하겠습니다.
\( V \) 및 \( R+j \omega L \)을 복소수 형태로 대체하고 (II)에 복소 형태로 쓰면 다음과 같이 쓸 수 있습니다.
\( I = \dfrac{V_0 e^{j\omega t}}{r e^{j\theta}} \)
위의 식을 지수 법칙을 사용하여 간소화하면
\( I = \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
오옴의 법칙을 사용하여 다음과 같이 쓸 수 있습니다.
\( V_R = R I = \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)

\( V_L = Z_L I = \dfrac{j V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
\( V_L \)에서 \( j \)를 지수 형태 \( j = e^{j \pi/2} \)로 쓰겠습니다
\( V_L = \dfrac{ e^{j \pi/2} V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
위의 식을 지수 법칙을 사용하여 다시 쓸 수 있습니다
\( V_L = \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t + \pi/2 -\theta)} \)
위에서 계산한 복소수를 사용하여 \( i \), \( v(t)_R \) 및 \( v(t)_L \)을 다음과 같이 계산할 수 있습니다.
실수 부분을 취하는 방식으로 다음과 같습니다:
\( i = \Re e I = \Re e \left( \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \right) \)
이는 다음과 같습니다.
\[ i = \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t-\theta) \] \( v(t)_R = \Re e V_R = \Re e \left( \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \right) \) \[ v(t)_R = \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t-\theta) \] \( v(t)_L = \Re e V_L = \Re e \left( \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t + \pi/2 -\theta)} \right) \) \[ v(t)_L = \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t + \pi/2 -\theta) \]

더 많은 참고 자료 및 링크