多変数関数の定義と、この関数の定義域の概念が例とともに示されています。
問題 とその 解答 も含まれています。
2変数の不等式系の解法 に関するスキルは、2変数関数の定義域を見つける際に必要です。
いくつかのよく知られた公式を考えてみましょう。
a) 辺の長さが \( x \) の正方形の周囲長 \( P \) は \( P = 4 x\) で与えられます。
b) 長さが \( L \)、幅が \( W \) の長方形の面積 \( A \) は \( A = L W \) で与えられます。
c) 2つの物体間のニュートンの万有引力の法則に基づく力 \( F \) は、質量 \( m_1 \)、\( m_2 \) が距離 \( d \) 離れているとき、次の式で与えられます: \( F = G \dfrac{m_1 m_2}{d^2} \)
ここで、\( G \) は定数です。
上記のa)の周囲長 \( P \) は、1つの変数 \( x \) の関数であると言えます。
b) の面積 \( A \) は、2つの変数 \( L \) と \( W \) の関数です。
c) の力 \( F \) は、3つの変数 \( m_1 \)、\( m_2 \)、\( d \) の関数です (注: G は定数です)。
\( n \) 個の変数 \( x_1, x_2, ...., x_n \) の関数 \( f \) とは、各 n 組の実数 \( x_1, x_2, ...., x_n \) に対して一意の実数 \( f (x_1, x_2, ...., x_n) \) を割り当てる規則のことを指します。
関数 \( f \) が一意に実数値を持つ \( x_1, x_2, ...., x_n \) の全ての n 組の実数の集合 \( D \) を、関数 \( f \) の定義域と呼びます。
\( u = f (x_1, x_2, ...., x_n) \) としたとき、定義域 \( D \) 内の全ての n 組に対応する \( u \) の値の集合を、\( f \) の値域と呼びます。 [1] , [2] , [3] 。
例 1 2変数関数
次のように定義された関数 \( f \) を考えます。
\[ f(x,y) = \sqrt{x^2+y^2} + \ln(x-y) \]
a) 計算せよ: \( f(4,3) \) 、 \( f(e^2,0) \)
b) \( f \) の定義域を求め、スケッチしなさい。
例 1 の解答
a)
\( f(4,3) \) を評価するには、\( x \) に \( 4 \)、\( y \) に \( 3 \) を代入します。
したがって、
\( f(4,3) = \sqrt{4^2+3^2} + \ln(4-3) \)
簡略化すると、
\( \quad = \sqrt{25} + \ln(1) = 5 + 0 = 5 \)
\( f(e^2,0) \) を評価するには、\( x \) に \( e^2 \)、\( y \) に \( 0 \) を代入します。
したがって、
\( f(e^2,0) = \sqrt{e^2 + 0^2} + \ln(e^2 - 0) \)
簡略化すると、
\( \quad = e + 2 \)
b)
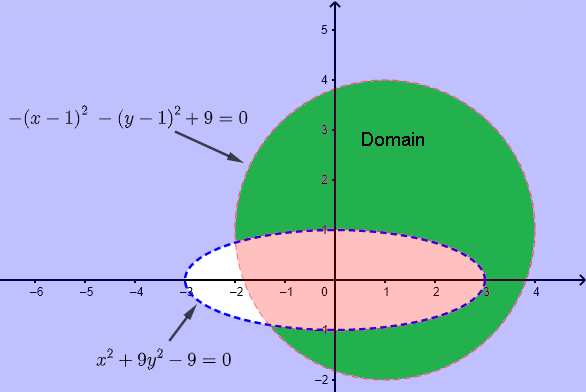
関数 \( f(x,y) \) の定義域を求めるには、次の条件を設定します:
1) \( \quad x^2+y^2 \ge 0 \) 、平方根の下の式は非負でなければなりません。
2) \( \quad x - y \gt 0 \) 、対数の引数は正でなければなりません。
条件 1) は常に満たされます。
条件 2) の不等式を解くと、次の図に示される解が得られます。

例 2 3変数関数
次のように定義された関数 \( g \) を考えます。
\[ g(x,y,z) = \sqrt{ x^2 + y^2 + z^2 - 9} \]
a) 計算せよ: \( g(3,-1,1) \)、 \( g(3/2,1/4,7/2) \)
b) \( g \) の定義域を求め、説明しなさい。
例 2 の解答
a)
\( g(3,-1,1) \) を評価するには、\( x \) に \( 3 \)、\( y \) に \( -1 \)、\( z \) に \( 1 \) を代入します。
したがって、
\( g(3,-1,1) = \sqrt{ 3^2 + (-1)^2 + 1^2 - 9} \)
簡略化すると、
\( \quad = \sqrt{2} \)
\( g(3/2,1/4,7/2) \) を評価するには、\( x \) に \( 3/2 \)、\( y \) に \( 1/4 \)、\( z \) に \( 7/2 \) を代入します。
したがって、
\( g(3/2,1/4,2) = \sqrt{ (3/2)^2 + (1/4)^2 + (7/2)^2 - 9} \)
簡略化すると、
\( \quad = \dfrac{\sqrt{89}}{4} \)
b)
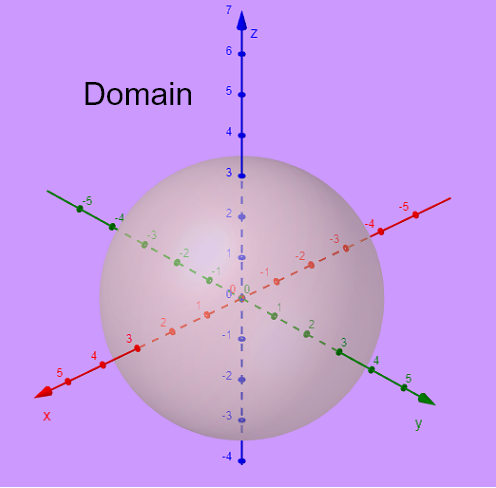
\( g(x,y,z) \) の定義域を求めるには、次の条件を設定します:
\( x^2 + y^2 + z^2 - 9 \ge 0 \) 、平方根の下の項は非負でなければなりません。
\( x^2 + y^2 + z^2 - 9 = 0 \) を考えると、これは \( x^2 + y^2 + z^2 = 3^2 \) と書き直せます。
したがって、\( x^2 + y^2 + z^2 - 9 = 0 \) の方程式のグラフは、半径が \( 3 \) で原点 \( (0,0,0) \) に中心を持つ球となります(下の図参照)。
例 3 2変数関数
次のように定義された関数 \( h \) を考えます。
\[ h(x,y) = \dfrac{1}{\ln (1 - x y) } - \sqrt{x - y^2}\]
a) \( h \) の定義域を求めて説明しなさい。
b) \( h \) の定義域に属する3つの順序対 \( (x,y) \) を示し、それらの点で関数を評価しなさい。
c) 定義域に属さない3つの順序対 \( (x,y) \) を示しなさい。
例 3 の解答
a)
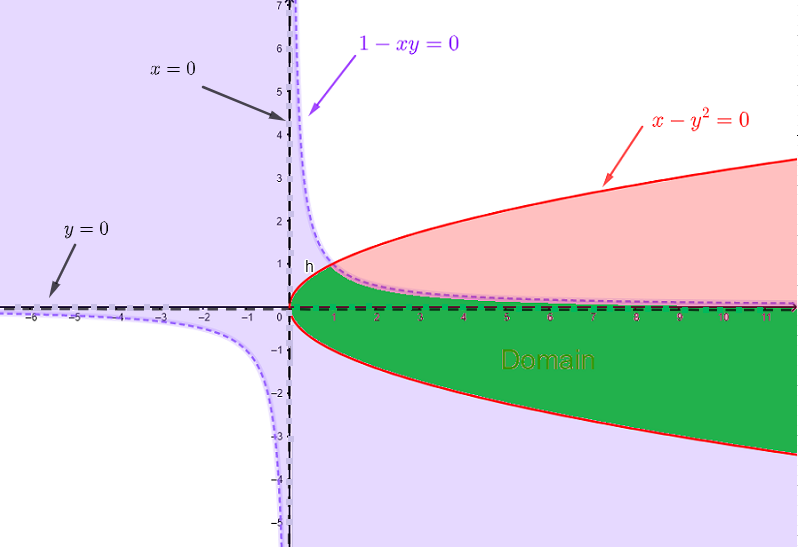
関数 \( h(x,y) \) の定義域を求めるには、次の条件を設定します:
1) \( \quad 1 - x y \gt 0 \) 、対数の引数は正でなければなりません。
2) \( \quad x - y^2 \ge 0 \) 、平方根の下の式は非負でなければなりません。
3) \( \quad \ln (1 - x y) \ne 0 \) つまり \( 1 - xy \ne 1 \) 、これは \( xy \ne 0 \) に相当し、対数の分母が 0 になってはいけません。
条件1)は、 \( 1 - x y = 0 \) つまり \( y = \dfrac{1}{x} \) をグラフ化し、不等式 \( 1 - x y \gt 0 \) を満たす点の集合を選択します(薄紫色の領域)。
条件2)は、 \( x - y^2 = 0 \) つまり \( x = y^2 \) をグラフ化し、不等式 \( x - y^2 \ge 0 \) を満たす点の集合を選択します(赤色の領域)。
条件3)は、軸上の点以外の任意の点で満たされます(軸上の破線)。
定義域は、条件1)、2)、3)の集合の交わりであり、\( x \) 軸または \( y \) 軸上の点を除いた緑色の領域です。
パートA
次の関数が与えられています:
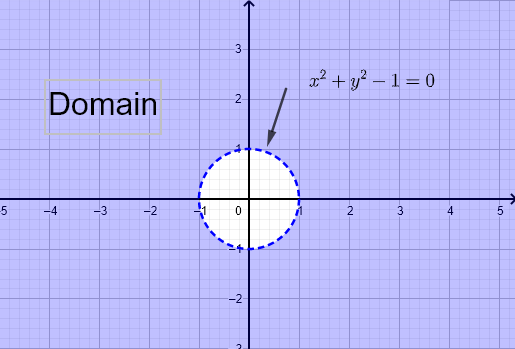
\( f (x,y) = \dfrac{1}{\sqrt{x^2 - y}} \) と \( g (x,y) = \ln (x^2 + y^2 - 1) \)
a) 各関数の定義域を求めなさい
b) 次の値を評価しなさい
1) \( f (1,0) \) , 2) \( g (1,-1) \) , 3) \( \dfrac{f(3,4)}{g(2,0)} \)
パートB
電気回路において、並列接続された3つの抵抗の抵抗値 \( R \) とそれぞれの抵抗値 \( r_1 , r_2 , r_3 \) は次の式で関係づけられます:
\( \dfrac{1}{R} = \dfrac{1}{r_1} + \dfrac{1}{r_2} + \dfrac{1}{r_3} \)
a) \( R \) を \( r_1 , r_2 , r_3 \) の関数として表しなさい。
b) \( r_1 = 100 \) 、\( r_2 = 50 \) 、\( r_3 = 20 \) のとき、\( R \) を計算しなさい。
パートC
次の関数の定義域を求めなさい:
a) \( f(x,y) = \sqrt{x^2+y-2x} \)
b) \( h(x,y) = \dfrac{\ln(x^2+9 y^2-9)}{\sqrt{7-x^2-y^2+2 x + 2 y}} \)
パートA
\( f (x,y) = \dfrac{1}{\sqrt{x^2 - y}} \) と \( g (x,y) = \ln (x^2 + y^2 - 1) \)
a)
関数 \( f \) の定義域は、次の条件を解いて求めます: \( x^2 - y \gt 0 \) 。分母はゼロであってはならず、平方根の引数は非負でなければなりません。
グラフ \( y = x^2 \) を描き、\( x^2 - y \gt 0 \) を満たす領域を選択します。以下の図にグラフィカルな解答が示されています。定義域は放物線 \( y = x^2 \) の外側にあるすべての点 \( (x,y) \) です。

パートB
a)
次の式が与えられています: \( \dfrac{1}{R} = \dfrac{1}{r_1} + \dfrac{1}{r_2} + \dfrac{1}{r_3} \)
すべての項を \( r_1 r_2 r_3 \) で掛けます。
\( \dfrac{r_1 r_2 r_3}{R} = \dfrac{r_1 r_2 r_3}{r_1} + \dfrac{r_1 r_2 r_3}{r_2} + \dfrac{r_1 r_2 r_3}{r_3} \)
簡略化すると、
\( \dfrac{r_1 r_2 r_3}{R} = r_2 r_3 + r_1 r_3 + r_1 r_2 \)
\( R \) を解くと、
\( R(r_1,r_2,r_3) = \dfrac{r_1 r_2 r_3}{r_2 r_3 + r_1 r_3 + r_1 r_2} \)
b)
\( R(100,50,20) = \dfrac{100 \times 50 \times 20}{50 \times 20 + 100 \times 20 + 100 \times 50} = 12.5\)
パートC
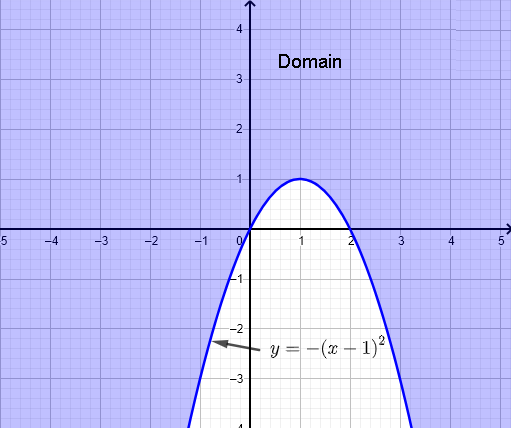
a) \( f(x,y) = \sqrt{x^2+y-2x} \)
関数 \( f(x,y) \) は平方根の引数が非負である場合に実数値をとるため、次の条件が必要です:
\( x^2+y-2x \ge 0 \)
平方完成を行い、次のように書き換えます:
\( (x-1)^2 - 1 + y \ge 0 \)
\( y \ge - (x-1)^2 + 1 \)
放物線 \( y = - (x-1)^2 + 1 \) をグラフに描き、関数 \( f \) の定義域を特定します。
定義域は、以下のグラフに示されているように、放物線 \( y = - (x-1)^2 + 1 \) の上または外側にある点 \( (x,y) \) の集合です(紫色)。