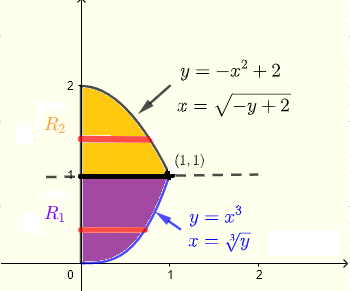目次
一般領域における二重積分
一般領域における二重積分の計算の例が示され、詳細な解答とともに説明されています。
重要な注意点
1) 一般的な非長方形領域に対してグラフや図を作成することは、二重積分を簡単にする第一歩です。
2) 一般的な領域で二重積分を計算するためには、次の4つのステップが必要です。
ステップ 1: 積分領域のグラフまたは図を作成する
ステップ 2: 垂直ストリップまたは水平ストリップを使用して領域を定義し、積分の順序を決定する
ステップ 3: 不等式を使って積分領域を記述する
ステップ 4: 積分を計算する
3) 次に示すように、与えられた積分領域 \( R \) を、無限の垂直ストリップとして記述し、積分を \( \displaystyle \iint_R f(x,y) \;dy \;dx \) と表現するか、水平ストリップとして記述し、積分を \( \displaystyle \iint_R f(x,y) \;dx \;dy \) と表現します。
一般領域における二重積分の計算
例1と例2の目的は、グラフや図を使って一般領域における積分の範囲を決定し、二重積分を計算することです。
例 1
問題: \( \displaystyle V = \iint_R (x^2+y) \;dy \;dx \) という二重積分を計算せよ。ただし、領域 \( R \) は、\(xy\) 平面上の三角形で、\(x\)-軸、\(y\)-軸、および直線 \( y = - x + 2 \) で囲まれている。
例 1 の解答
一般領域での二重積分を計算するための4つの主要なステップがあります。
ステップ 1 積分領域を表すグラフまたは図を作成する
まず、領域 \( R \) のグラフまたは図を作成します。この例では、三角形は \(x\) 軸、\(y\) 軸、そして直線 \( y = - x + 2 \) によって定義されます。
この三角形は、原点と直線 \( y = - x + 2 \) の \(x\) 軸および \(y\) 軸との交点、すなわち \( (2,0) \) および \( (0,2) \) で定義されます。

この領域での積分を計算する方法は2つあります。
ステップ 2 ストリップを使用して領域を定義する方法を決定する
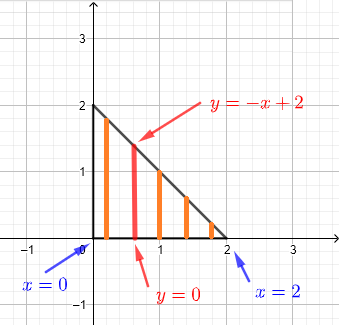
1) 垂直ストリップを使用して領域 \( R \) を記述します。以下の図のように、領域 \( R \) を無限の垂直ストリップの集合として考えます。
任意の \( x \) における垂直ストリップは、\( y = 0 \) から \( y = - x + 2 \) まで延びます。すべてのストリップを含むためには、\( x \) は \( x = 0 \) から \( x = 2 \) の範囲で値を取る必要があります。したがって、積分領域 \( R \) は次のように定義されます:
ステップ 3 不等式を使用して領域を記述する
\( R \) : \( 0 \le x \le 2 \) , \( 0 \le y \le - x + 2 \)
ステップ 4 積分を計算する
積分は次のように書き換えられます:
\( \displaystyle V = \int_0^2 \int_0^{-x+2} (x^2+y) \;dy \;dx \)
\( = \displaystyle \int_0^2 ( -x^3 +\dfrac{5}{2} x^2 - 2x + 2) \;dx = 8/3\)
次に、水平ストリップを使用して同じ問題に答えます。
ステップ 1 は上記と同じです。
ステップ 2 ストリップを使用して領域を定義する方法を決定する
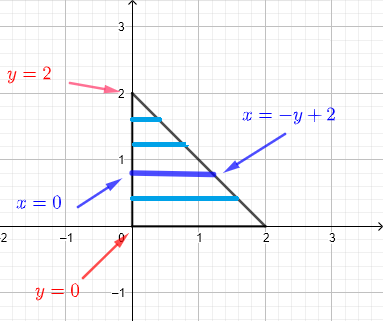
2) 水平ストリップを使用して領域 \( R \) を記述します。以下の図のように、領域 \( R \) を無限の水平ストリップの集合として考えます。
任意の \( y \) における水平ストリップは、\( x = 0 \) から \( x = - y + 2 \) まで延びます。すべてのストリップを含むためには、\( y \) は \( y = 0 \) から \( y = 2 \) の範囲で値を取る必要があります。したがって、積分領域 \( R \) は次のように定義されます:
ステップ 3 不等式を使用して領域を記述する
\( R \) : \( 0 \le x \le - y + 2 \) , \( 0 \le y \le 2 \)
ステップ 4 積分を計算する
積分は次のように書き換えられます:
\( \displaystyle V = \int_0^2 \int_0^{-y+2} (x^2+y) \;dx \;dy \)
\( = \displaystyle \int_0^2 (-\dfrac{1}{3} y^3 + y^2 - 2 y + \dfrac{8}{3} ) \;dy = 8/3 \)
注意 いずれの場合も、変数を含む積分は内側の積分です。
次に、水平ストリップを使用して同じ問題に答えます。
ステップ 1 は上記と同じです。
ステップ 2 ストリップを使用して領域を定義する方法を決定する
2) 下図のように、水平ストリップを使用して領域 \( R \) を記述します。
領域 \( R \) を無限の水平ストリップの集合と見なします。
任意の水平ストリップは、ある \( y \) の値で \( x = 0 \) から \( x = - y + 2 \) まで延びます。領域 \( R \) を記述するすべてのストリップを含めるためには、\( y \) は \( y = 0 \) から \( y = 2 \) の範囲で値を取る必要があります。したがって、積分領域 \( R \) は次のように定義されます:
ステップ 3 不等式を使って積分領域を記述する
\( R \) : \( 0 \le x \le - y + 2 \) , \( 0 \le y \le 2 \)

ステップ 4 積分を計算する
したがって、積分は次のように表されます:
\( \displaystyle V = \int_0^2 \int_0^{-y+2} (x^2+y) \;dx \;dy \)
\( = \displaystyle \int_0^2 (-\dfrac{1}{3} y^3 + y^2 - 2 y + \dfrac{8}{3} ) \;dy = 8/3 \)
注意 どちらの場合でも、変数を含む積分は内側の積分です。
例 2
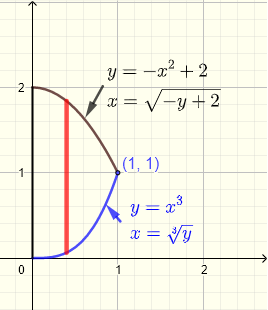
問題: \( \displaystyle V = \iint_R (x+y) \;dy \;dx \) という二重積分を計算せよ。ただし、領域 \( R \) は、\(xy\) 平面上で \(y\)-軸、曲線 \( y = x^3 \) と \( y = - x^2 + 2 \) によって囲まれた領域とする。
例 2 の解答
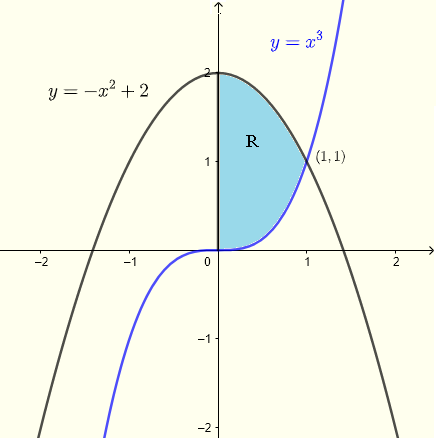
まず、領域 \( R \) を解析します。下図に示すように、2つの曲線は、連立方程式の解として求まる点で交わります。
\( y = x^3 \)
\(y = - x^2 + 2 \)
上記の連立方程式を解くための一つの方法は、2つの方程式を引き算して \( y \) を消去し、\( x \) だけの方程式に簡略化することです。次の方程式が得られます:
\( 0 = x^3 + x^2 - 2 \)
グラフを参考にすると、\( x = 1 \) がこの方程式の解であることがわかります。これは解析的に確認することもできます。
2つの曲線の交点の \(y\) 座標は、すでに見つけた解 \( 1 \) を曲線の式に代入して求められます。\( y = (1)^3 = 1 \) です。
したがって、交点は \( (1,1) \) となります。
1) 垂直ストリップを使用する場合
垂直ストリップは、曲線 \( y = x^3 \) 上から始まり、曲線 \( x = - x^2 + 2 \) まで延びます。領域全体では、\( x \) は \( x = 0 \) から \( x = 1 \) までの値を取ります。したがって、積分領域 \( R \) は次のように定義されます:
\( R \) : \( 0 \le x \le 1 \) , \( x^3 \le y \le - x^2 + 2 \)
したがって、積分は次のように計算されます:
\( \displaystyle V = \int_0^1 \int_{x^3}^{-x^2+2} (x+y) \;dy \;dx = \dfrac{803}{420}\)
2) 水平ストリップを使用する場合
水平ストリップは \( y \)-軸上の \( x = 0 \) から始まり、曲線 \( x = \sqrt[3]y \) または曲線 \( x = \sqrt{- y + 2} \) まで延びます。このため、領域 \( R \) を2つの部分 \( R_1 \) と \( R_2 \) に分割することができます。
領域 \( R_1 \) では、\( y \) は \( y = 0 \) から \( y = 1 \) までの値を取り、領域 \( R_2 \) では \( y = 1 \) から \( y = 2 \) までの値を取ります。
したがって、積分領域 \( R \) は次の2つの部分に分けられます:
\( R_1 \) : \( 0 \le x \le \sqrt[3]y \) , \( 0 \le y \le 1 \)
そして
\( R_2 \) : \( 0 \le x \le \sqrt{- y + 2} \) , \( 0 \le y \le 1 \)
したがって、積分は次のように計算されます:
\( \displaystyle V = \iint_{R_1} (x+y) \;dx \;dy + \iint_{R_2} (x+y) \;dx \;dy \)
\( \displaystyle = \int_0^1 \int_{0}^{\sqrt[3]y} (x+y) \;dx \;dy + \int_1^2 \int_{0}^{\sqrt{-y+2}} (x+y) \;dx \;dy = \dfrac{803}{420}\)
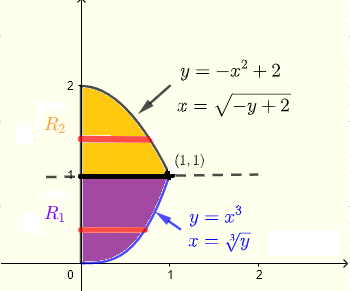
問題に応じて積分順序の選択が必要な例
例 3、4、5 では、二重積分では通常の積分順序の選択肢がない場合があることを示します。
例 3、4、5 の目的は、グラフや図を使って、二重積分の解析計算につながる積分の順序を決定することです。
例 3
問題: 可能であれば、次の二重積分 \( \displaystyle V = \int _0^1 \int _y^1 (y + e^{-x^2}) dx dy \) を計算しなさい。計算するために積分の順序を変更する必要がある場合は、その順序を逆にしなさい。
例 3 の解答
まず、内側の積分から始めます。
\( \displaystyle I = \int _y^1 (y+e^{-x^2}) dx \)
上記の \( I \) を評価しようとすると、\( \displaystyle I = \int _y^1 (e^{-x^2}) dx \) は解析的に計算することができません。
与えられた積分範囲によると、積分 \( V \) の積分領域 \( R \) は次のように記述できます:
\( R \) : \( y \le x \le 1 \) , \( 0 \le y \le 1 \)
これは、水平ストリップの集合として下図に示されます。
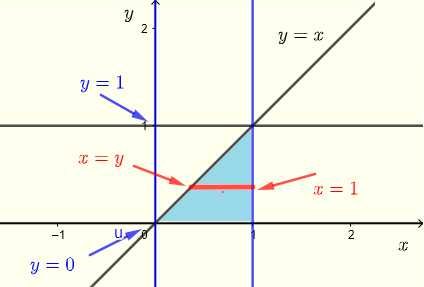
次に、領域 \( R \) を垂直ストリップを使って記述し、下図に示します。
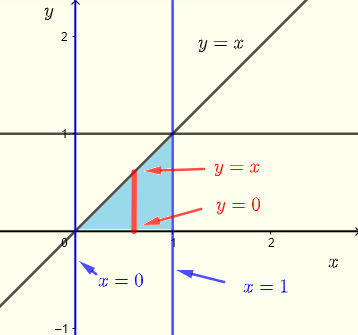
グラフを使って積分領域 \( R \) を確認し、積分の順序を変更することで計算できるかどうか検討します。
\( R \) : \( 0 \le x \le 1 \) , \( 0 \le y \le x \)
積分 \( V \) は次のように書き換えられます:
\( \displaystyle V = \int _0^1 \int _0^x (y + e^{-x^2}) dy dx \)
内側の積分 \( I \) を評価します。
\( \displaystyle I = \int _0^x (y + e^{-x^2}) dy \)
\( = \left[ \dfrac{y^2}{2} + y e^{-x^2} \right]_0^x \)
\( = \dfrac{x^2}{2} + x e^{-x^2} \)
これを \( V \) に代入し、積分を計算します。
\( \displaystyle V = \int _0^1 (\dfrac{x^2}{2} + x e^{-x^2} ) dx \)
\( = \left[ \frac{x^3}{6}-\frac{1}{2}e^{-x^2} \right]_0^1 \)
\( = \dfrac{2}{3} - \dfrac{1}{2}e^{-1} \)
例 4
領域 \( R \)(下図の青い部分)上での二重積分 \( \displaystyle V = \iint_R \left(\sqrt{1+y^3}+\:x\right)\:dy \:dx \) を評価しなさい。
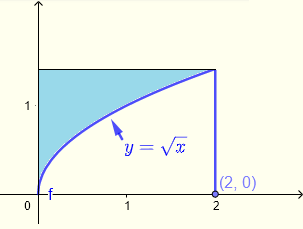
例 4 の解答
内側の積分 \( \displaystyle I = \int \left(\sqrt{1+y^3}+\:x\right) \; dy \) を行います。
この積分は解析的に容易にはできないことがすぐにわかります。
そこで、積分の順序を入れ替えます。
\( V = \displaystyle \iint_R \left(\sqrt{1+y^3}+\:x\right)\:dx \:dy \)
領域 \( R \) は次のように記述できます:
\( R\) : \( 0 \le x \le y^2 \) , \( 0 \le y \le \sqrt 2 \)
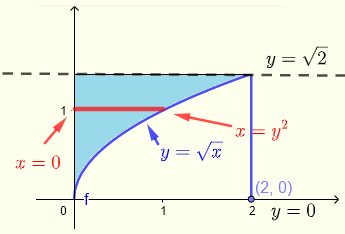
\( \displaystyle V = \int _0^{\sqrt 2} \int _0^{y^2} \left(\sqrt{1+y^3}+\:x\right) dx dy \)
内側の積分 \( I \) を評価します。
\( I = \displaystyle \int _0^{y^2} \left(\sqrt{1+y^3}+\:x\right) dx \)
\( = \left [ x \sqrt{1+y^3} + \dfrac{x^2}{2} \right]_0^{y^2} \)
評価して簡略化します。
\( = y^2\sqrt{y^3+1}+\frac{y^4}{2} \)
これを \( V \) に代入し、外側の積分を計算します。
\( \displaystyle V = \int _{0\:}^{\sqrt 2} \left(y^2\sqrt{y^3+1}+\frac{y^4}{2} \right) \; dy \)
上記の積分を計算します。
\( \displaystyle V = \left [ \frac{2}{9}\left(y^3+1\right)^{\frac{3}{2}}+\frac{y^5}{10} \right]_0^{\sqrt 2} \)
簡略化します。
\( V = \frac{2}{9}\left(\left(\sqrt{2}\right)^3+1\right)^{\frac{3}{2}}+\frac{\left(\sqrt{2}\right)^5}{10}-\dfrac{2}{9} \approx 2.00 \)
例 5
二重積分を評価する: \( \displaystyle V = \iint_R (x+y)\:dydx \) ただし、領域 \( R \) は曲線 \( x = (y-2)^2-2 \) と \( y = - x + 6 \) によって囲まれています。
例 5 の解法
垂直ストリップを使用すると、積分の領域は 2 つの部分に分かれます。なぜなら、 \( y \) の限界は区間 \( -2 \le x \le 2 \) と \( 2 \le x \le 7 \) で異なるからです。この方法で積分を計算するのは非常に難しいです。
そこで、水平ストリップを使用します。
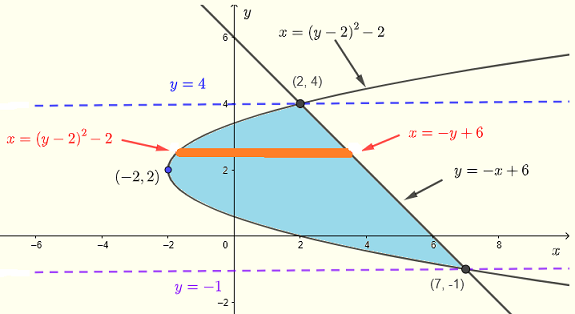
領域 \( R \) は次のように記述できます:
\( R\) : \( (y-2)^2 - 2 \le x \le -y+6 \) , \( -1 \le y \le 4 \)
\( \displaystyle V = \int _{-1}^{4} \int _{(y-2)^2 - 2}^{-y+6} (x+y)\:dx \: dy \)
内側の積分を \( \displaystyle I = \int _{(y-2)^2 - 2}^{-y+6} (x+y)\:dx \) とします。
上記の積分を計算します。
\( I = \dfrac{-y^4+6y^3-13y^2+12y+32}{2} \)
この結果を \( V \) に代入し、外側の積分を計算します。
\( \displaystyle V = \int _{-1}^4 \left( \dfrac{-y^4+6y^3-13y^2+12y+32}{2} \right) \; dy \)
上記の積分を計算します。
\( \displaystyle V = \dfrac{1}{2} \left[-\dfrac{y^5}{5}+\dfrac{3y^4}{2}-\dfrac{13y^3}{3}+6y^2+32y\right]_{-1}^4 \)
評価結果:
\( V = \dfrac{875}{12} \)
注
練習として、垂直ストリップを使用して次の二重積分が得られることを確認してください:
\( \displaystyle \int _{-2}^2\:\int _{2-\sqrt{x+2}}^{2+\sqrt{x+2}}\:\left(x+y\right)dydx+\int _2^7\:\int _{2-\sqrt{x+2}}^{-x+6}\:\left(x+y\right)dydx \)
他の問題と解答
パート 1
-
二重積分の限界を次のように記述しなさい: \( \displaystyle V = \iint_R x y \;dy \;dx \) および \( \displaystyle V = \iint_R x y \;dx \;dy \)、ただし領域 \( R \) は \( xy\)-平面上にあり、\(x \ge 0\) および \(y \ge 0\)、曲線 \( x^2 + y^2 = 1 \) によって囲まれています。そしてそれを評価しなさい。
-
二重積分の限界を次のように記述しなさい: \( \displaystyle V = \iint_R \sin(x^2) \;dy \;dx \) および \( \displaystyle V = \iint_R \sin(x^2) \;dx \;dy \)、ただし領域 \( R \) は頂点 \( A(0,0)\) , \( B(3,0) \) , \( C(3,3) \) によって形成された三角形である。そしてそれを評価しなさい。
パート 2
次の積分を評価しなさい: \( \displaystyle V = \int _0^1 \int _{ \arcsin y}^{\frac{\pi }{2}}\:\left(xy\right)dxdy \)
上記の問題の解答
パート 1:
-
積分領域
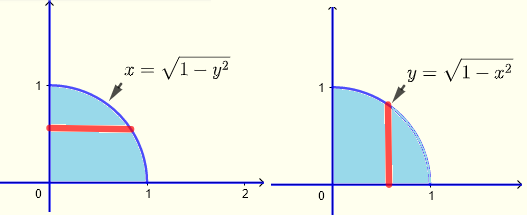
垂直ストリップ
\( 0 \le x \le 1 \) , \( 0 \le y \le \sqrt{1-x^2} \)
\( \displaystyle \int _0^1\:\int _0^{\sqrt{1-x^2}}\:xy\:dy\:dx = 1/8 \)
水平ストリップ
\( 0 \le x \le \sqrt{1-y^2} \) , \( 0 \le y \le 1 \)
\( \displaystyle \int _0^1\:\int _0^{\sqrt{1-y^2}}\:xy\:dx\:dy = 1/8\)
-
積分領域

垂直ストリップ
\( 0 \le x \le 3\) , \( 0 \le y \le x \)
\( \displaystyle \int _0^3\:\int _0^x \:\sin(x^2)\:dy\:dx = \dfrac{1}{2}\left(-\cos \left(9\right)+1\right) \)
水平ストリップ
\( y \le x \le 3 \) , \( 0 \le y \le 3 \)
\( \displaystyle \int _y^3\:\int _0^3\:\sin(x^2)\:dx\:dy \) 解析的に解くのは非常に困難です。
パート 2:
\( \displaystyle V = \int _0^1 \int _{ \arcsin y}^{\frac{\pi }{2}}\:\left(xy\right)dxdy \)
内側の積分 \( I \) を次のように計算します。
\( \displaystyle I = \int _{ \arcsin y}^{\frac{\pi }{2}}\:\left(xy\right)dx \)
\( = y \left(\dfrac{\pi^2}{8} - \dfrac{\arcsin^2(y)}{2} \right) \)
\( I \) を積分 \( V \) に代入します。
\( \displaystyle V = \int _0^1 (y \left(\dfrac{\pi^2}{8} - \dfrac{\arcsin^2(y)}{2} \right)) dy \)
解析的に解くのは非常に困難です。
そこで、積分の順序を入れ替えます。
まず、積分領域 \( R \) をグラフで描きます。
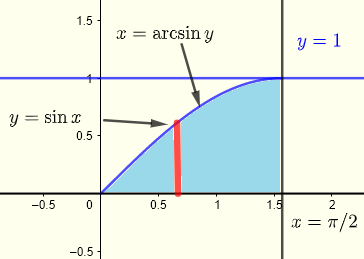
\( \displaystyle V = \int _0^{\frac{\pi }{2}} \int _0^{\sin x} x \; y \; dy \;dx \)
内側の積分 \( I = \int _0^{\sin x} x \; y \; dy \) を計算します。
\( I = x\frac{\sin ^2\left(x\right)}{2} \)
\( \sin^2(x) = \dfrac{1-\cos(2x)}{2} \)
\( I = \dfrac{x}{4}(1-\cos(2x)) \)
\( I \) を \( V \) に代入します。
\( \displaystyle V = \int _0^{\frac{\pi }{2}} (\dfrac {x}{4} - \dfrac {x}{4} \cos (2x)) dx \)
被積分関数を分けます。
\( \displaystyle = \int _0^{\frac{\pi }{2}} \dfrac {x}{4} dx - \int _0^{\frac{\pi }{2}} \dfrac {x}{4} \cos (2x) dx \)
右側の積分は部分積分の技法を使用して次のようになります。
\( = \left[ \frac{x^2}{8} \right]_0^{\pi/2}- \left[\frac{1}{8} x \sin (2x)+\frac{1}{16}\cos (2x) \right]_0^{\pi/2} \)
評価結果:
\( = \dfrac{\pi^2+4}{32} \)
他の参考文献とリンク
- 二重積分の計算
- Howard Anton, Irl C. Bivens, ステップhen Davis ; Calculus: Early Transcendentals; Willey, 2012.
- Gilbert Strang; MIT, Calculus, Wellesley-Cambridge Press, 1991
- Joel Hass, University of California, Davis; Maurice D. Weir Naval Postgraduate School; George B. Thomas, Jr.Massachusetts Institute of Technology ; University Calculus , Early Transcendentals, Third Edition
, Boston Columbus , 2016, Pearson.
解答付き工学数学の例と解法