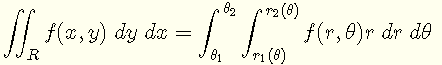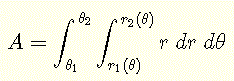問題: 平面 \( xy \)-平面上の原点を中心とし、半径が \( 1 \) の円で囲まれた領域 \( R \) において、二重積分 \( \displaystyle V = \iint_R \sqrt {1 - x^2 - y^2} \;dy \;dx \) を計算せよ。
例 1 の解答
与えられた積分は長方形座標にありますが、基本的な関数を使って解くことはできません。そこで、極座標に変換してみましょう。
\( f(x,y) = \sqrt {1 - x^2 - y^2} \) とし、極座標で表現します。
-example-1.gif)
\( r^2 = x^2 + y^2 \)
したがって、関数 \( f(x,y) \) を極座標に変換すると次のようになります。
\( f(r,\theta) = \sqrt {1 - r^2} \)
積分領域 \( R \) は円であり、次の不等式で定義されます:
\( R: \) \( 0 \le \theta \le 2\pi \) および \( 0 \le r \le 1 \)
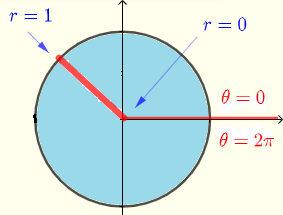
与えられた積分を長方形座標から極座標に変換すると、次のようになります。
\( \displaystyle V = \iint_R \sqrt {1 - x^2 - y^2} \;dy \;dx = \int_0^{2\pi} \int_0^{1} \sqrt{1-r^2} \; r \; dr \; d\theta \)
内積分を \( I \) と定義します。
\( \displaystyle I = \int_0^{1} \sqrt{1-r^2} \; r \; dr \)
\( = \left[ -\frac{1}{3}\left(1-r^2\right)^{\frac{3}{2}} \right]_0^1 = \dfrac{1}{3} \)
\( I \) を代入し、\( V \) を計算します。
\( \displaystyle V = \int_0^{2\pi} (1/3) \; d\theta \)
\( = \dfrac{1}{3} \left[ \theta \right]_0^{2\pi} \)
\( = \dfrac{2\pi}{3} \)