二重積分を使用して、平面 \( z = 0 \) と放物面 \( z = 4 - x^2 - y^2 \) の間にある立体の体積を計算します。
解答 例 1
平面 \( z = 0 \) と放物面の間の立体が下図に示されています。
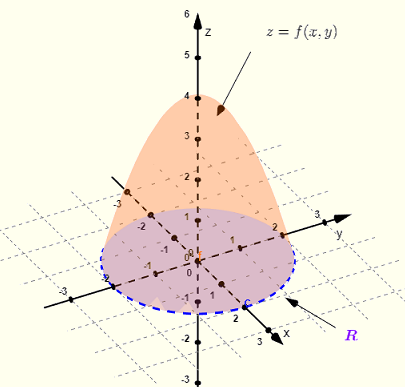
\( 0 = 4 - x^2 - y^2 \)
標準形に書き直すと、
\( x^2 + y^2 = 2^2 \)
これは中心が \( (0,0) \) で半径が \( 2 \) の円です。
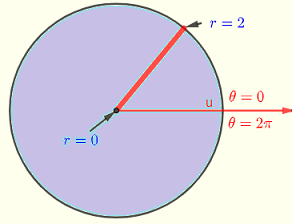
体積 \( V \) は、次の二重積分で計算されます。
\( V = \displaystyle \iint_R f(x,y) \;dy \;dx \) , ここで \( R \) は次のように定義される積分領域です。
\( R: 0\le \theta \le 2\pi , 0 \le r \le 2 \)
これは図2に示される円であり、\( f(x,y) = z = 4 - x^2 - y^2 \) です。
極座標では、体積は次のように表されます。
\( \displaystyle V = \int_0^{2\pi} \int_0^2 (4-r^2) r dr d\theta \)
\( \displaystyle V = \int_0^{2\pi} \int_0^2 (4-r^2) r dr d\theta \)
\( = \int_0^{2\pi} \left[2r^2-\frac{r^4}{4}\right]_0^2 d\theta \)
\( = \int_0^{2\pi} ( 4 ) d\theta \)
\( = 8 \pi \)