パルス \( f(t) \) とその フーリエ変換 \( F(\omega) \) を視覚化するためのインタラクティブなオンライングラフ計算機を提供しています。 \( t \) は時間であり、\( \omega \) は角周波数です。
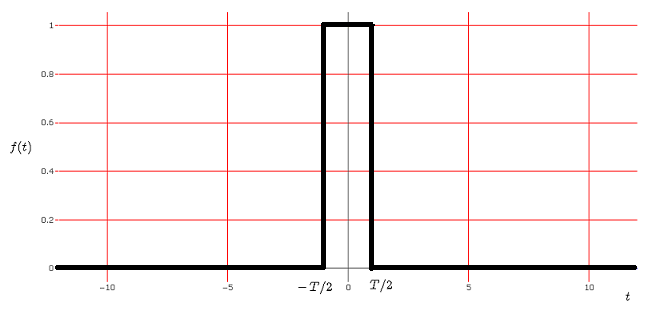\( f(t) \) のフーリエ変換は次のように定義されます。
\[ F(\omega) = \int_{-\infty}^{+\infty} f(t) e^\left( - j \omega t\right) dt \\
= \int_{-T/2}^{+T/2} 1 \cdot e^\left( - j \omega t\right) dt \\
= \left[ \dfrac{ e^\left( - j \omega t \right)}{-j \omega} \right]^{T/2}_{-T/2}
\]
計算し、簡略化すると次のようになります。
\[ F(\omega) = \dfrac{\sin(\omega(T/2))}{\omega/2}
\]
T =