AC回路の問題を解決 - 解答付き

目次

キルヒホッフの法則とオームの法則を拡張し、複素形式のインピーダンスを使用してAC回路の問題を解決します。
電圧、電流、インピーダンスなどのすべての量は、標準および複素数で表され、極形式で表されます。

複素数の復習

虚数単位は、\( j = \sqrt {-1} \) または \( j^2 = - 1 \)として定義されます。
標準形の複素数 \( Z \) は、\( Z = a + j b \) の形で表され、極形式では次のように書き直すことができます。
\( Z = r \; \angle \; \theta \)
ここで、\( r \)と\( \theta \)はそれぞれ、\( Z \)のモジュラスと偏角であり、次のように定義されます。
\( r = |Z| = \sqrt {a^2 + b^2} \) および \( \theta = \arctan \left( \dfrac{b}{a} \right) \) の範囲 \( -\pi \lt \theta \le \pi \) 内で定義されます。
複素数の乗算や除算は、極形式のほうが容易です。
\( Z_1 = r_1 \; \angle \; \theta_1 \) および \( Z_2 = r_2 \; \angle \; \theta_2 \) とした場合
\( Z_1 \cdot Z_2 = r_1 \cdot r_2 \; \angle \; \theta_1 + \theta_2 \)
\( \dfrac{Z_1}{Z_2} = \dfrac{r_1}{r_2} \; \angle \; \theta_1 - \theta_2 \)

問題と解答

問題 1
以下の回路において、電圧源 \( v_i = 10 \cos (\omega t ) \) V、抵抗値 \( R = 100 \; \Omega \)、コンデンサ \( C = 0.47 \; \mu F \)、周波数 \( f = 1 \) kHz、および \( \omega = 2 \pi f \)が与えられています。抵抗 \( R \)とコンデンサ \( C \)にかかる電流の大きさと位相シフト（極形式）を求めなさい。

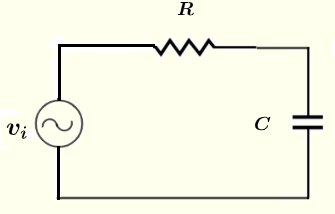
問題 1 の解答
\( V_i \)、\( V_R \)、\( V_C \)、および \( I \) をそれぞれ \( v_i \)、\( v_R \)、\( v_C \)、および \( i \) の複素形式とします。


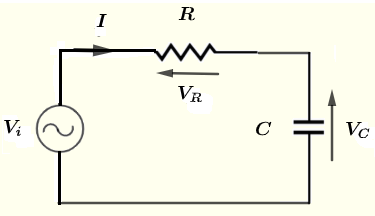
ループ内の電圧に対するキルヒホッフの法則を使用して、次の式を書きます。
\( V_i - V_R - V_C = 0\)      (1)
抵抗 \( R \) およびコンデンサ \( C \) の複素インピーダンスは次のように与えられます。
\( Z_R = R \; \)       (実数)
\( Z_C = - j \dfrac{1}{\omega C} \; \)       (虚数)

オームの法則を使用して次のように書きます。
\( V_R = Z_R I \) および \( V_C = Z_C I \)
式 (1) に \( V_R \) と \( V_C \) を代入します。
\( V_i - Z_R I - Z_C I = 0 \)
これを解いて \( I \) を求めます。
\( I = \dfrac{V_i}{Z_R + Z_C} \)

オームの法則を使用して \( V_R \) および \( V_C \) を次のように計算します。
\( V_R = Z_R I = \dfrac{V_i Z_R }{Z_R + Z_C} \)

\( V_C = Z_C I = \dfrac{V_i Z_C }{Z_R + Z_C} \)


複素極形式では、\( v_i = 10 \cos (\omega t ) \) は次のように書くことができます。
\( V_i = 10 \; \angle \; 0 \)

次に、上記の式に \( V_i \)、\( Z_R \)、および \( Z_C \) を代入して次のように書き直します。
\( I = \dfrac{10 \; \angle \; 0}{R - j \dfrac{1}{\omega C}} \)

\( V_R = \dfrac{10 R \; \angle \; 0 \; }{R - j \dfrac{1}{\omega C}} \)

\( V_C = \dfrac{ (10 \; \angle \; 0 \;) (- j \dfrac{1}{\omega C}) }{R - j \dfrac{1}{\omega C}} \)

分母を \( Z_D = R - j \dfrac{1}{\omega C} \) とし、複素形式で書き直します。
\( Z_D \) のモジュラス：\( | Z_D | = \sqrt {R^2 + \dfrac{1}{\omega^2 C^2}} \)

\( Z_D \) の偏角：\( \phi = \arctan \dfrac{-\dfrac{1}{\omega C}}{R} = \arctan \dfrac{-1}{R \omega C} \)

次に、複素量 \( - j \dfrac{1}{\omega C} \) を極形式で書き直します。
\( - j \dfrac{1}{\omega C} = \dfrac{1}{\omega C} \; \angle \; -\dfrac{\pi}{2} \)

次に、\( I \)、\( V_R \)、および \( V_C \) に極形式の複素量を代入して書き直します。
\( I = \dfrac{10 \; \angle \; 0}{{ | Z_D | \; \angle \; \phi}} \)

\( V_R = \dfrac{10 R \; \angle \; 0 \; }{ | Z_D | \; \angle \; \phi} \)

\( V_C = \dfrac{10 \; \angle \; 0 \; (\dfrac{1}{\omega C} \; \angle \; -\dfrac{\pi}{2}) }{{ | Z_D | \; \angle \; \phi}} \)

次に簡略化します。

\( I = \dfrac{10} { | Z_D | } \; \angle \; - \phi \)

\( V_R = \dfrac{10 R}{ | Z_D |} \; \angle \; - \phi \)

\( V_C = \dfrac{10}{ \omega C | Z_D | } \; \angle \; -\dfrac{\pi}{2}- \phi \)

次に、すべての既知の量を数値に置き換えます。
\( \omega = 2 \cdot \pi \cdot f = 2 \cdot \pi 10^3 = 2000 \pi \)
\( | Z_D | = \sqrt {R^2 + \dfrac{1}{\omega^2 C^2}} = \sqrt {100^2 + \dfrac{1}{(2000 \pi)^2 (0.47 \cdot 10^{-6})^2}} = 353.08 \; \Omega \)
\( \phi = \arctan \dfrac{-\dfrac{1}{\omega C}}{R} = \arctan \dfrac{-\dfrac{1}{2000 \pi \cdot 0.47 \cdot 10^{-6} }}{100} = -73.55^{\circ} \)
したがって、

\( I = \dfrac{10} { | Z_D | } \; \angle \; - \phi = 0.0283 \; \angle \; 73.55^{\circ} \)
\( I \) の大きさは \( 0.02832 \; A\) で、位相シフトは \( 73.55^{\circ} \) です。

\( V_R = \dfrac{10 R}{ | Z_D |} \; \angle \; - \phi = 2.832 \; \angle \; 73.55^{\circ} \)
\( V_R \) の大きさは \( 2.832 \; V\) で、位相シフトは \( 73.55^{\circ} \) です。

\( V_C = \dfrac{10}{ \omega C | Z_D | } \; \angle \; -\dfrac{\pi}{2}- \phi = 9.591 \; \angle \; -16.45^{\circ} \)
\( V_C \) の大きさは \( 9.591 \; V\) で、位相シフトは \( -16.45^{\circ} \) です。

問題 2

次の回路において、電圧源 \( v_i = 10 \cos (\omega t ) \; V \)、抵抗 \( R = 100 \; \Omega \)、コンデンサ \( C = 0.47 \; \mu F \)、インダクタ \( L = 300 \; mH \)、周波数 \( f = 2 \) kHz および \( \omega = 2 \pi f \)が与えられています。電圧 \( v_o \) の大きさと位相シフト（極形式）を求めなさい。


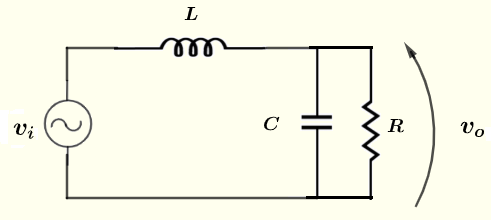
問題 2 の解答
\( I \)、\( V_i \)、および \( V_0 \) をそれぞれ \( i \)、\( v_i \)、および \( v_o \) の複素形式とします。
\( V_i \) は極形式で次のように書けます。
\( V_i = 10 \; \angle \; 0 \)
抵抗 \( R \) のインピーダンスは次のように与えられます。
\( Z_R = R \; \)
コンデンサ \( C \) のインピーダンスは次のように与えられます。
\( Z_C = - j \dfrac{1}{\omega C} \; \)
抵抗 \( R \) とコンデンサ \( C \) は並列接続されています。\( R \) と \( C \) に相当するインピーダンス \( Z \) は次のように与えられます。

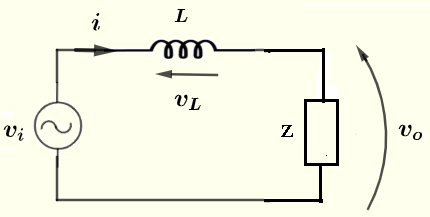
\( Z = \dfrac{Z_R \cdot Z_C}{Z_R + Z_C} \)
インダクタ \( L \) の複素インピーダンス \( Z_L \) は次のように与えられます。
\( Z_L = j \omega L \)
ループ内の電圧に対するキルヒホッフの法則を使用して、次の式を書きます。
\( V_i - V_L - V_0 = 0\)      (1)
オームの法則を使用して次のように書きます。
\( V_L = Z_L I \) および \( V_0 = Z I \)
式 (1) に \( V_L \) および \( V_0 \) を代入します。
\( V_i - Z_L I - Z I = 0 \)
これを解いて \( I \) を求めます。
\( I = \dfrac{V_i}{ Z_L + Z} \)
オームの法則を使用して次のように書きます。
\( V_o = Z I = \dfrac{Z}{ Z_L + Z} V_i\)
既知の量を代入して数値を求めます。
\( \omega = 2 \pi f = 2 \pi \cdot 2000 = 4000 \pi \)
\( Z_R = R = 100 \)
\( Z_C = - j \dfrac{1}{\omega C} = - j \dfrac{1}{4000 \pi \cdot 0.47 \cdot 10^{-6}} = - 169.314 j \)

\( Z = \dfrac{R \cdot Z_C}{R + Z_C} \) (\( R \) と \( C \) が並列接続されている場合)

\( = \dfrac{100 \cdot (- 169.314 j)}{100 - 169.314 j } = 74.138 -43.787 j\)
そして
\( Z_L = j \omega L = 4000 \pi \cdot 300 \cdot 10^{-3} j = 3769.911 j \)
\( V_o = \dfrac{Z}{ Z_L + Z} V_i \)

簡略化します。
\( = (-0.01135 -0.02012 j) V_i \)
複素数 \( (-0.01135 -0.02012 j) \) を極形式で書き直し、極形式の \( V_i \) に代入します。
\( = ( 0.02310 \angle -119.43^{\circ} ) (10 \; \angle \; 0) \)
簡略化します。
\( V_o = 0.23 \; \angle \; -119.43^{\circ} \)

問題 3

次の回路において、電圧源 \( v_i = 10 \cos (\omega t ) \; V \)、抵抗 \( R_1 = 220 \; \Omega \)、\( R_2 = 2.2 \; k\Omega \)、\( R_3 = 1 \; k\Omega \)、\( C_1 = 0.47 \; \mu F \)、\( C_2 = 1.5 \; \mu F \)、インダクタ \( L = 30\; mH \)、周波数 \( f = 2.5 \) kHz および \( \omega = 2 \pi f \) が与えられています。電圧 \( v_o \) の大きさと位相シフト（極形式）を求めなさい。

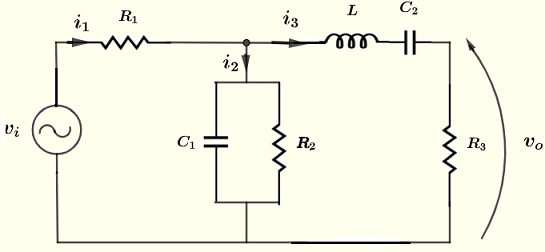
問題 3 の解答
\( I_1 \)、\( I_2 \)、\( I_3 \)、\( V_i \)、および \( V_0 \) をそれぞれ \( i_1 \)、\( i_2 \)、\( i_3 \)、\( v_i \)、および \( v_o \) の複素形式とします。
\( V_i \) は次のように極形式で書くことができます。
\( V_i = 10 \; \angle \; 0 \)
\( V_o \) はオームの法則を使用して次のように計算できます。
\( V_o = R_3 I_3\)
したがって、\( I_3 \) を計算する必要があります。
回路図に示すように、インピーダンスをグループ化します。
\( Z_1 = R_1 \)
\( Z_2 = \dfrac{R_2 ( - \dfrac{1}{\omega C_1} j)}{R_2 - \dfrac{1}{\omega C_1} j} \)      (\( C_1 \) と \( R_2 \) は並列接続)
\( z_3 = R_3 + j \omega L - \dfrac{1}{ \omega C_2} j \)      (\( C_2 \)、\( L \) と \( R_3 \) は直列接続)

キルヒホッフの電圧法則を2つの閉ループに適用して2つの方程式を書きます。
\( V_i - V_{z_1} - V_{z_2} = 0 \)
\( V_{z_2} - V_{z_3} = 0 \)
オームの法則を適用して \( V_{z_1} = Z_1 I_1 \)、\( V_{z_2} = Z_2 I_2 \)、および \( V_{z_3} = Z_3 I_3 \) を書き、これを上記の方程式に代入して電流のみを含む方程式を得ます。
\( V_i - Z_1 I_1 - Z_2 I_2 = 0 \)     (1)
\( Z_2 I_2 - Z_3 I_3 = 0 \)     (2)
次に、ノードAでキルヒホッフの電流法則を使用して次のように書きます。
\( I_1 = I_2 + I_3 \)     (3)
これで、未知数 \( I_1 \)、\( I_2 \)、および \( I_3 \) を持つ3つの方程式がありますが、必要なのは \( I_3 \) だけです。
式 (3) を使用して、式 (1) の \( I_1 \) を \( I_2 + I_3 \) に置き換え、\( I_1 \) を方程式から排除し、2つの未知数を持つ方程式の系を得ます。
\( V_i - Z_1 ( I_2 + I_3) - Z_2 I_2 = 0 \)     (4)
\( Z_2 I_2 - Z_3 I_3 = 0 \)     (5)
次に、標準形に書き直します。
\( (Z_1 + Z_2 ) I_2 + Z_1 I_3 = V_i \)     (4)
\( Z_2 I_2 - Z_3 I_3 = 0 \)     (5)
行列式を使用して上記の方程式の系を解きます。
\( I_3 = \dfrac{\begin{vmatrix} Z_1 + Z_2 & V_i \\ Z_2 & 0 \end{vmatrix}}{\begin{vmatrix} Z_1 + Z_2 & + Z_1 \\ Z_2 & -Z_3 \end{vmatrix}} \)
行列式を評価して次のようにします。
\( I_3 = \dfrac{Z_2}{(Z_1+Z_2)Z_3 + Z_1 Z_2} V_i \)

数値計算
\( \omega = 2 \pi f = 5000 \pi \)
\( Z_1 = 220 \)
\( Z_2 = \dfrac{2200 ( - \dfrac{1}{5000 \pi \cdot 0.47 10^{-6}} j)}{2200 - \dfrac{1}{5000 \pi \cdot 0.47 10^{-6}} j} \)

\( Z_2 = 8.30804 -134.93950 j \)

\( z_3 = 1000 + 5000 \pi \cdot 30 \cdot 10^{-3} j - \dfrac{1}{ 5000 \pi \cdot 1.5 \cdot 10^{-6}} j \)
\( Z_3 = 1000 + 428.79757 j \)
\( I_3 = (0.00013 - 0.00043 j)V_i = 0.00044 \angle -73.18^{\circ} \cdot 10 \angle 0\)
\( V_0 = R_3 I_3 = 1000 \cdot 0.00044 \angle -73.18^{\circ} \cdot 10 \angle 0 \)
簡略化します。
\( V_0 = 4.4 \angle -73.18^{\circ} V \)

その他の問題と解答

問題 4
次の条件が与えられています： \( v_i = 10 \angle 0^{\circ} \)、\( R = 200 \; \Omega \)、\( C = 0.47 \; \mu F \)、\( L = 40 \; mH \)、周波数 \( f = 1 \) kHz。
複素形式でインダクタを通る電流 \( I \) とインダクタにかかる電圧 \( V_0 \) を求めなさい。

問題 4 の解答

解答: \( I = 0.047 \angle -47.84^{\circ}\) 、\( V_0 = 11.38 \angle 42.16^{\circ} \)

問題 5
次の条件が与えられています： \( v_i = 10 \angle 0^{\circ} \)、\( R_1 = 100 \; \Omega \)、\( C = 0.47 \; \mu F \)、\( R_2 = 120 \; \Omega \)、\( R_3 = 200 \; \Omega \)、\( R_4 = 400 \; \Omega \)、\( L = 20 \; mH \)、周波数 \( f = 2 \) kHz。
複素形式で各抵抗にかかる電圧と電流 \( I_1 \)、\( I_2 \)、\( I_3 \) を求めなさい。

問題 5 の解答
解答
電流：\( I_1 = 0.054 \angle 10.55^{\circ} \; 、 \; I_2 = 0.048 \angle 23.01^{\circ} \; 、 \; I_3 = 0.013 \angle -42.22^{\circ} \)
電圧：\( V_{R_1} = 5.49 \angle 10.55^{\circ} \; 、 \; V_{R_2} = 4.71 \angle -12.32^{\circ} \; 、 \; V_{R_3} = 2.60 \angle -42.22^{\circ} \; 、 \; V_{R_4} = 2.77 \angle 15.63^{\circ} \)

その他の参考文献とリンク