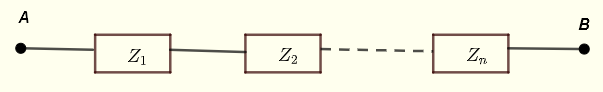
点AとBの間の等価インピーダンスは次のように与えられます。
\[ Z_{AB} = Z_1 + Z_2 + ... + Z_n\]
ここでは、複素インピーダンスを使用して、AC回路における直列および並列インピーダンスの等価インピーダンスを計算する方法について説明します。すべてのステップは記号計算を使用して示され、その後に数値が使用されます。
AC回路では電流に\( i \)という記号を使用するため、ここでは虚数単位として\( j \)を使用し、\( j^2 = -1 \) または \( j = \sqrt{-1} \) と定義します。
次のように、直列に接続されたインピーダンスを\( Z_1 \) 、\( Z_2 \) ... \( Z_n \)とします。
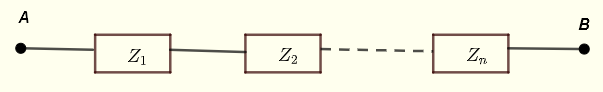
点AとBの間の等価インピーダンスは次のように与えられます。
\[ Z_{AB} = Z_1 + Z_2 + ... + Z_n\]
例1
以下に示す直列RLC回路に対する複素インピーダンスを求めなさい。与えられている値は以下の通りです:
周波数\( f = 1 \; kHz \) 、\( C = 10 \; \mu F \) 、\( L = 10 \; mH \)、および \( R = 100 \; \Omega \)

問題1の解答
次のように設定します:
\( Z_R = R \) 、 \( Z_C = \dfrac{1}{j \omega C} = \dfrac{-j}{\omega C} \) 、\( Z_L = j \omega L\)
直列回路のインピーダンスの規則を適用します:
\( Z_{AB} = Z_R + Z_C + Z_L = R - \dfrac{j}{\omega C} + j \omega L \)
次のように設定します:
\( X_L = \omega L = 2 \pi f L \) および \( X_C = \dfrac{1}{\omega C} = \dfrac{1}{2 \pi f C} \)
そして、 \( Z_{AB} \) を次のように書き直します:
\( Z_{AB} = R + j(X_L - X_C) \)
数値を代入します。
\( X_L = \omega L = 2 \pi f L = 2 \pi 10^3 \times 10^{-2} = 62.83 \Omega \)
\( X_C = \dfrac{1}{\omega C} = \dfrac{1}{2 \pi f C} = \dfrac{1}{2 \pi 10^3 \times 10^{-5} } = 15.92 \Omega \)
虚数項をまとめます。
\( Z_{AB} = 100 + j ( 62.83 - 15.92 ) \)
簡略化します。
\( Z_{AB} = 100 + j ( 62.83 - 15.92 ) = 100 + 46.91 j\)
上記を指数形式で表します。
\( Z_{AB} = \sqrt {100^2 + 46.91^2} e^{j \arctan{\dfrac{46.91}{100}}} = 110.45 e^{j 0.44} \)
\( Z_{AB} \) はファゾー形式で次のように書かれます。
\( Z_{AB} = 110.45 \angle 0.44 \; rad = 110.45 \angle 25.13^{\circ} \)
直列RLC回路インピーダンス計算機を使用して、さらに練習することができます。
次のように、並列に接続されたインピーダンスを\( Z_1 \) 、\( Z_2 \) ... \( Z_n \)とします。
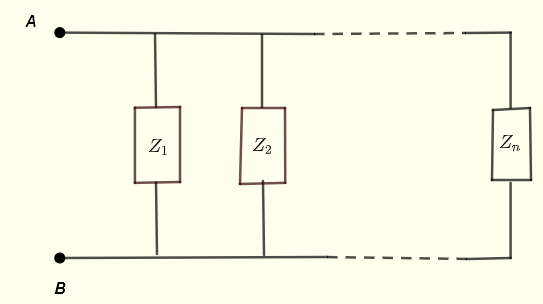
点AとBの間の等価インピーダンスは次のように与えられます。
\[ \dfrac{1}{Z_{AB}} = \dfrac{1}{Z_1} + \dfrac{1}{Z_2} + ... + \dfrac{1}{Z_n} \]
例2
以下に示す並列RLC回路に対する複素インピーダンスを求めなさい。与えられている値は以下の通りです:
周波数\( f = 1.5 \; kHz \) 、\( C = 15 \; \mu F \) 、\( L = 20 \; mH \)、および \( R = 50 \; \Omega \)

問題2の解答
次のように設定します:
\( Z_R = R \) 、\( Z_C = \dfrac{1}{j \omega C} \)、\( Z_L = j \omega L\)
並列回路のインピーダンスの規則を適用します。
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{Z_R} + \dfrac{1}{Z_C} + \dfrac{1}{Z_L} \)
\( = \dfrac{1}{R} + \dfrac{1}{\dfrac{1}{j \omega C}} + \dfrac{1}{j \omega L} \)
次のように設定します:
\( X_L = \omega L \) および \( X_C = \dfrac{1}{\omega C} \)
そして、上記を次のように書き直します:
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{R} + \dfrac{1}{\dfrac{X_C}{j}} + \dfrac{1}{j X_L} \)
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{R} + \dfrac{j}{{X_C}} - j \dfrac{1}{ X_L} \)
\( = \dfrac{1}{R} + j (\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} ) \)
上記の複素数のモジュラス\( r \)は次のように与えられます。
\( r = \sqrt { (\dfrac{1}{R})^2 + (\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} )^2} \)
その偏角\( \alpha \)は次のように与えられます。
\( \alpha = \arctan \left(\dfrac{\dfrac{1}{{X_C}} - \dfrac{1}{ X_L}}{\dfrac{1}{R}} \right) \)
\( = \arctan \left(\dfrac{R}{X_C}-\dfrac{R}{X_L} \right) \)
次に、複素数の指数形式を使用して次のように書きます。
\( \dfrac{1}{Z_{AB}} = r e^{j\alpha} \)
次に、等価インピーダンス\( Z_{AB} \)を指数形式で複素数として次のように書きます。
\( Z_{AB} = \dfrac{1}{r} e^{-j \alpha} \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} e^{-j \arctan \left(\dfrac{R}{X_C}-\dfrac{R}{X_L} \right) } \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} e^{j \arctan \left(\dfrac{R}{X_L}-\dfrac{R}{X_C} \right) } \)
次に、与えられた値を使用します。
\( f = 1.5 \; kHz \) 、\( C = 15 \; \mu F \) 、\( L = 20 \; mH \)、および \( R = 50 \; \Omega \)
\( X_L = \omega L = 2 \pi f L = 2 \pi 1.5 \times 10^3 \times 20 \times 10^{-3 } = 188.50 \)
\( X_C = \dfrac{1}{\omega C} = \dfrac{1}{ 2\pi f C} = \dfrac{1}{ 2\pi 1.5 \times 10^3 \times 15 \times 10^{-6}} = 7.07\)
モジュラス: \( \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{50}\right)^2 + \left(\dfrac{1}{{7.07}} - \dfrac{1}{ 188.50} \right)^2}} \)
\( = 7.27 \)
偏角: \( \arctan \left(\dfrac{R}{X_L}-\dfrac{R}{X_C} \right) \)
\( = \arctan \left(\dfrac{50}{188.50}-\dfrac{50}{7.07} \right) \)
\( = - 81.64^{\circ} \)
並列RLC回路インピーダンス計算機を使用して、さらに練習することができます。