直列共振RLC回路

目次

共振 直列RLC回路と共振周波数、カットオフ周波数の公式が展開され、帯域幅と品質係数が定義されます。また、例題と詳細な解説も含まれています。 \( \) \( \) \( \) \( \)
以下では、大文字の \( I \) は実電流 \( i \) の複素（極）形式を、大文字の \( V_i \) は実電圧 \( v_i \) の複素（極）形式を表します。
共振直列RLC回路計算機を使用して、以下の例題の計算を確認したり、これらの回路のさらなる練習や調査に役立てることができます。

A - 直列共振RLC回路

以下に示す直列RLC回路を考えます。

周波数 \( f \) の電圧源によって供給される回路では、直列RLC回路の総インピーダンス \( Z \) は次のように与えられます：
\[ Z = R + j \left(\omega L - \dfrac{1}{\omega C} \right) \]
電流 \( I \) と電圧 \( V_i \) の関係は次のように与えられます：
\[ I = \dfrac{V_i}{Z} \]
ここで、\( V_i \) と \( I \) はそれぞれ電圧 \( v_i \) と電流 \( i \) の複素形式です。
複素数の絶対値の定義を使用すると、インピーダンスの大きさ \( |Z| \) は次のように表されます：
\( |Z| = \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} \)
電圧源のピーク値が \( V_0 \) で、電圧源が \( v_i = V_0 \cos (\omega t) \) で与えられる場合、\( I \) のピーク値 \( I_0 \) は次のように与えられます：
\( I_0 = \dfrac{V_0}{ |Z| } = \dfrac{V_0}{ \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} } \)
共振周波数は、\( I_0 \) が最大になる、または \( Z \) の大きさが最小になる周波数として定義されます。
抵抗 \( R \) は周波数に依存しないため、\( |Z| \) の最小値は \( \omega = \omega_r \) のときに発生し、その条件は次のようになります：
\( \left(\omega_r L - \dfrac{1}{\omega_r C} \right) = 0 \)
上記の式を \( \omega_r \) について解くと、共振周波数は次のようになります：
\[ \omega_r = \dfrac{1}{\sqrt {L C}} \quad \quad (I) \]
共振周波数 \( \omega = \omega_r \) のとき、
1) \( Z = R \)
電圧源のピーク値が \( V_0 \) のとき、\( I \) のピーク値 \( I_0 \) は次のように与えられます：
2) \( I_0 = \dfrac{V_0}{R} \)
\( X_L = \omega L \) および \( X_C = \dfrac{1}{\omega C} \) とすると、
3) \( X_L = X_C \)

例 1
上記の直列RLC回路で、\( R=300 \; \Omega \)、\( L = 100 \; mH \)、\( C = 100 \mu F \) の場合、
a) 共振周波数 \( \omega_r \) を求めなさい。
b) \( |Z| \)、\( X_L = \omega L \)、\( X_C = \dfrac{1}{\omega C} \)、および \( I_0 \) を周波数 \( \omega \) の関数としてグラフ化し、そのグラフを考察しなさい。

例 1 の解答
a)
共振周波数 \( \omega_r \) は次のように与えられます：
\( \omega_r = \dfrac{1}{\sqrt {L C}} = \dfrac{1}{\sqrt{100\times10^{-3} \times 100 \times 10^{-6}}} \approx 316.23\)
b)
以下に \( |Z| \)、\( X_L \)、および \( X_C \) のグラフを示します。
グラフから、\( |Z| \) の最小値は \( R = 300 \; \Omega \)（点A）であることがわかります。
\( X_L \) と \( X_C \) のグラフは交差しており（点B）、したがって \( X_L = X_C \) または \( \left(\omega_r L - \dfrac{1}{\omega_r C} \right) = 0 \) となります。



以下のグラフは電流 \( I_0 \) を示しており、共振周波数 \( \omega_r \approx 316.23\)（小数点以下2桁に四捨五入後）で最大となります。

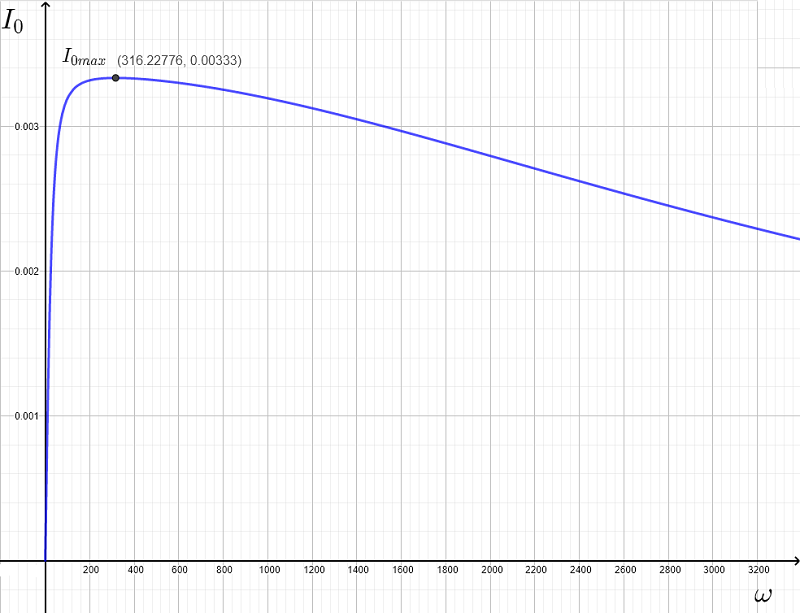
B - 共振回路における平均電力

直列RLC回路に供給される平均電力 \( P_a \) は次のように与えられます： \[ \displaystyle \quad \quad P_a = \dfrac{V_0^2}{2 |Z|} \cos \theta \quad \quad (II) \] ここで、\( \theta \) はインピーダンス \( Z = R + j \left(\omega L - \dfrac{1}{\omega C} \right) \) の引数であり、次のように与えられます。
\( \theta = \arctan \left( \dfrac{ \omega L - \dfrac{1}{\omega C} }{R} \right) \)
逆三角関数の性質を使用すると、次のようになります。
\( \tan \theta = \left( \dfrac{ \omega L - \dfrac{1}{\omega C} }{R} \right) \)
\( \theta \) は、以下に示す直角三角形の鋭角と見なすことができます（角度の接線の定義を使用すると、上記のように \( \tan \theta \) を得ることができます）。



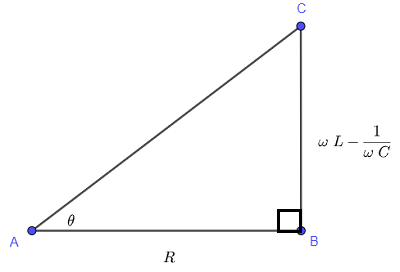
同じ三角形を使用して力率 \( \cos \theta \) を計算します。
三角形の斜辺は次のように計算されます。
\( AC = \sqrt {R^2 + \left( \omega L - \dfrac{1}{\omega C} \right)^2} \)
\( \cos \theta = \dfrac{AB}{AC} = \dfrac{R}{\sqrt {R^2 + \left( \omega L - \dfrac{1}{\omega C} \right)^2}} \)
上記の公式 (II) に \( \cos \theta \) と \( |Z| \) を代入し、電力 \( P_a \) を次のように表します：
\( \displaystyle \quad \quad P_a = \dfrac{V_0^2}{2 \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} }\dfrac{R}{\sqrt {R^2 + \left( \omega L - \dfrac{1}{\omega C} \right)^2}} \)
簡略化すると
\[ \displaystyle \quad \quad P_a = \dfrac{V_0^2 R}{2 \left({R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} \right) } \quad \quad (III) \]
共振周波数 \( \omega_r = \dfrac{1}{\sqrt {LC}} \) のとき、\( \left(\omega_r L - \dfrac{1}{\omega_r C} \right) = 0 \) となり、電力は最大値に達し、次のようになります：\[ P_{a max} = \dfrac{V_0^2}{2 \; R} \quad \quad (IV) \]

C - 共振回路のカットオフ周波数と品質係数

次に、カットオフ周波数を、(III) 式での電力 \( P_a(\omega) \) が最大電力 \( P_{a max} \) の半分となる周波数 \( \omega_c \) と定義します。
したがって、次の方程式を解く必要があります：
\( P_a (\omega_c ) = \dfrac{1}{2} \left(\dfrac{V_0^2}{2 \; R} \right) \)

\( \dfrac{V_0^2 R}{2 \left({R^2 + \left(\omega_c L - \dfrac{1}{\omega_c C} \right)^2} \right) } = \dfrac{1}{2} \dfrac{V_0^2}{2 \; R} \)
簡略化すると次のようになります：
\( \dfrac{ R}{2 \left({R^2 + \left(\omega_c L - \dfrac{1}{\omega_c C} \right)^2} \right) } = \dfrac{1}{4 R} \)
両辺を交差させて簡略化し、上記の方程式を次のように書き直します：
\( (\omega_c L - \dfrac {1}{\omega_c C } ) = R^2 \)
平方根を取って解を求めると、次の2つの方程式が得られます：
\( \omega_c L - \dfrac {1}{\omega_c C} = \pm R \)
すべての項に \( \omega_c C \) を掛けて簡略化します：
\( \omega_c^2 L C - 1 = \pm \omega_c R C \)
標準形の2次方程式として書き直します：
\( \omega_c^2 L C \pm \omega_c R C - 1 = 0\)
最初の2次方程式 \( \quad \omega_c^2 L C + \omega_c R C - 1 = 0\) を解いて次の2つの解を得ます：
\( \omega_{c1} = \dfrac {- R C \pm \sqrt{ (R C)^2 + 4 L C }}{ 2 L C } \)

2番目の2次方程式 \( \quad \omega_c^2 L C - \omega_c R C - 1=0\) を解いて次の2つの解を得ます：
\( \omega_{c2} = \dfrac {R C \pm \sqrt{ (R C)^2 + 4 L C}}{ 2 L C } \)
合計で4つの解が得られます。ここで、\( \sqrt{ (R C)^2 + 4 L C } \) の値は \( RC \) よりも大きいため、カットオフ周波数は正の値であることから、2つの解のみが有効です。
カットオフ周波数 \( \omega_{c1} \) および \( \omega_{c2} \) は次のように与えられます：
\( \omega_{c1} = \dfrac {- R C + \sqrt{ (R C)^2 + 4 L C }}{ 2 L C } \)

\( \omega_{c2} = \dfrac {R C + \sqrt{ (R C)^2 + 4 L C}}{ 2 L C } \)
すでに共振周波数 \( \omega_r = \dfrac{1}{\sqrt{LC}} \) を求めています。
簡単な代数を使用して、\( \omega_{c1} \) および \( \omega_{c2} \) を \( \omega_r \) の式で書き換えます：
\[ \omega_{c1} = - \dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} \quad \quad (V) \]
\[ \omega_{c2} = \dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} \quad \quad (VI) \]

注：
\[ \omega_{c1} \times \omega_{c2} = \omega_r^2 \quad \quad (VII) \]

共振回路の帯域幅は、次のように定義されます： \( \Delta \omega = \omega_{c2} - \omega_{c1} \)

品質係数 \( Q \) は次のように定義されます：
\( Q = \dfrac{\omega_r}{\Delta \omega} \)
代入すると
\( Q = \dfrac {\omega_r} { \left(\dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} - \left(-\dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} \right) \right)} \)
簡略化すると
\[ Q = \omega_r \dfrac{L}{R} \quad \quad (VIII) \]

D - 詳細な解説付きの追加の例

例 3
ある直列RLC共振回路が、下限と上限のカットオフ周波数として \( f_{c_1} = 650 \) ヘルツと \( f_{c_2} = 950 \) ヘルツを持つように設計されています。
a) 抵抗 \( R \) が \( 30 \Omega \) である場合、コンデンサ \( C \) の静電容量とインダクタ \( L \) のインダクタンスを計算しなさい。
b) 回路の品質係数はどのくらいですか？

例 3 の解答
a)
角周波数を計算します。
\( \omega_{c_1} = 2 \pi f_{c_1} = 1300 \pi \) rad/s
\( \omega_{c_2} = 2 \pi f_{c_1} = 1900 \pi \) rad/s
上記で展開した式 (VII) を使用して、回路の共振周波数 \( \omega_{r} \) を計算します。
\( \omega_{r} = \sqrt {\omega_{c_1} \times \omega_{c_2}} = \sqrt {1300 \pi \times 1900 \pi } = 100 \sqrt{247} \pi = 4937.400 \) rad/s
\( \omega_{c_2} - \omega_{c_1} = \dfrac{R}{L} \)
したがって
\( L = \dfrac{R } {\omega_{c_2} - \omega_{c_1}} = \dfrac{30} {1900 \pi - 1300 \pi } = 0.01591 \) H
\( \omega_{r} = \dfrac{1}{\sqrt {L C} } \)
したがって
\( C = \dfrac{1}{\omega_{r}^2 L} = \dfrac{1}{(100 \sqrt{247} \pi)^2 \times 0.01591} = 2.5783 \times 10^{-6} \) F

b)
品質係数は次のように与えられます：
\( Q = \dfrac{\omega_{r}}{\omega_{c_2} - \omega_{c_1}} = \dfrac{100 \sqrt{247} \pi}{1900 \pi - 1300 \pi } = 2.62\)

参考文献およびリンク

• 共振直列RLC回路計算機
• 直列RLC回路
• 直列RLC回路のインピーダンス計算機
• 並列RLC回路のインピーダンス計算機
• 直列RLC回路の電流グラフ作成計算機