直列RLC回路における電流と電圧の計算

目次

ここでは、複素インピーダンスを使用して、直列RLC回路の電流と電圧を解析する方法について説明します。複素数は、交流回路におけるインピーダンス、電流、および電圧の計算を大幅に簡略化します。
交流回路では、記号 \( i \) は電流を表すため、ここでは \( j \) を虚数単位として使用し、\( j^2 = -1 \) または \( j = \sqrt{-1} \) と定義します。
実数値の電流と電圧には小文字を使用し、複素数形式の電流と電圧には大文字を使用します。

A - 直列RLC回路における複素数としてのインピーダンスとファゾール

周波数 \( f \) の電源によって供給される回路において、各RLCコンポーネントのインピーダンスは以下のように与えられます。
抵抗 \( R \) の抵抗値 \( Z_R \) の複素形式インピーダンスは次のように表されます。 \[ Z_R = R \] インダクタンス \( L \) のインダクタ \( Z_L \) の複素形式インピーダンスは、インダクティブリアクタンスとも呼ばれ、次のように表されます。 \[ Z_L = j \omega L \] 容量 \( C \) のコンデンサ \( Z_C \) の複素形式インピーダンスは、キャパシティブリアクタンスとも呼ばれ、次のように表されます。 \[ Z_C = - \dfrac{1}{\omega C} j \] ここで、\( \omega = 2 \pi f \) です。
最も重要な点は、インダクティブおよびキャパシティブリアクタンスが電源電圧の周波数に依存することです。

\( V_i \)、\( I \)、\( V_R \)、\( V_L \)、および \( V_C \) をそれぞれ \( v_i \)、\( i \)、\( v_R \)、\( v_L \)、および \( v_C \) の複素形式とします。
キルヒホッフの電圧法則を複素インピーダンスに拡張して次のように記述します。
\( V_i - V_R - V_L - V_C = 0\)     (1)
オームの法則を複素インピーダンスに拡張して次のように記述します。
\( V_R = Z_R I \)
\( V_L = Z_L I \)
\( V_C = Z_C I \)
これらを方程式 (1) に代入して次のように求めます。
\( V_i = Z_R I + Z_L I + Z_C I = 0\)
これを解いて \( I \) を求めます。
\( I = \dfrac{V_i}{Z_R + Z_L + Z_C } \)
直列RLC回路の複素インピーダンスの合成値を \( Z \) とし、次のように定義します。
\[ Z = Z_R + Z_L + Z_C = R + j \left(\omega L - \dfrac{1}{\omega C} \right) \]
インピーダンス \( Z \) の<Ａ href="http://www.analyzemath.com/complex/modulus-argument.html">絶対値: \[ |Z| = \sqrt{R^2 + \left(\omega L - \dfrac{1}{\omega C}\right)^2} \]
インピーダンス \( Z \) の<Ａ href="http://www.analyzemath.com/complex/modulus-argument.html">偏角: \[ \theta = \arctan \left( \dfrac {\omega L - \dfrac{1}{\omega C}}{R} \right) \]
インピーダンス \( Z \) の絶対値と偏角は、電源電圧の周波数 (\( \omega = 2 \pi f \)) に依存することに注意してください。この性質はフィルタの設計や他の多くの電子回路で有用です。
\( Z \) を極形式で表します。
\[ Z = |Z| \; \angle \; \theta \]
上記で行った \( Z_R, Z_L, Z_C \) および \( Z \) の式は、以下に示すようにファゾールを使用して幾何学的に解釈できます。


(a) では、実部を水平軸に、虚部を垂直軸にプロットして、\( Z_R \)、\( Z_L\) および \( Z_C \) を表示します。
(b) では、\( Z = Z_R + Z_L + Z_C \) をベクトル（または複素数）の加法を使用して幾何学的にプロットします。
(c) では、ピタゴラスの定理を使用して、\( Z \) の絶対値を表す斜辺を持つ直角三角形：\( |Z| = \sqrt{R^2 + \left(\omega L - \dfrac{1}{\omega C}\right)^2} \) を描画します。これは、複素数を使用して上で得られた結果と全く同じです。
同様にして、角度：\( \theta = \arctan \left (\dfrac{\omega L - \dfrac{1}{\omega C}}{R} \right) \)

B - 直列RLC回路の電流と電圧

\( v_i = V_0 cos ( \omega t) \) とし、\( V_0 \) を電源電圧のピーク値とします。
オイラーの複素数公式：
\( e^{j \omega t} = \cos (\omega t) + j \sin (\omega t )\)
したがって \( v_i \) は次のようにも書くことができます。
\( v_i \) は \( e^{j \omega t} \) の実部に等しいです。
ここでは「実部」の部分を省略し、すべての計算を複素数で行い、複素形式で \( V_i \) を次のように定義します。
\( V_i = V_0 e^{j \omega t} \)
そして、複素形式での \( I \) を導出します。
\( I = \frac{V_0 e^{j\omega t}}{|Z| \; \angle \; \theta} \)
そして、極形式での \( I \) は次のように表されます。
\( I = \dfrac{V_0}{|Z|} \; \angle \; \omega t - \theta \)
\( I = I_0 \; \angle \; \omega t - \theta \) , ここで \( I_0 = \dfrac{V_0}{|Z|} \)
インピーダンス \( Z_R, Z_L\) および \( Z_C \) を極形式で再び書きます。
\( Z_R = R = R \; \angle \; 0 \)
\( Z_L = j \omega L = \omega L \; \angle \; \pi/2\)
\( Z_C = - \dfrac{1}{\omega C} j = \dfrac{1}{\omega C} \; \angle \; - \pi/2\ \)
電圧は次のように与えられます。
\( V_R = Z_R I = (R \; \angle \; 0) (I_0 \; \angle \; {\omega t - \theta}) = R I_0 \angle \; \omega t - \theta \)
\( V_L = Z_L I = (\omega L \; \angle \; \pi/2) (I_0 \; \angle \; {j\omega t - \theta}) = \omega L I_0 \; \angle \; {\omega t - \theta + \pi/2} \)
\( V_C = Z_C I = (\dfrac{1}{\omega C} \; \angle \; - \pi/2) (I_0 \; \angle \; {j\omega t - \theta}) = \dfrac{I_0}{\omega C} \; \angle \; {\omega t - \theta - \pi/2} \)
電流 \( I \) と電圧 \( V_R \), \( V_C \), および \( V_C \) は、ファゾールを使用して以下に示します。

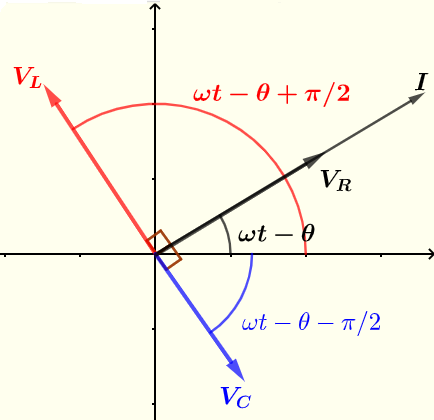
実際の電流と電圧は、上記で得られた複素（または極）形式の電流と電圧の実部により与えられます。
\( i = \dfrac{V_0}{|Z|} \cos( \omega t - \theta) \)

\( v_R = R \dfrac{V_0}{|Z|} \cos(\omega t - \theta) \)

\( v_L = \omega L \dfrac{V_0}{|Z|} \cos(\omega t - \theta + \pi/2) \)

\( v_C = \dfrac{V_0}{\omega C|Z|} \cos(\omega t - \theta - \pi/2) \)

注意 計算中に時間変化 \( \omega t \) を省略し、電流と電圧を時間の関数として表現する必要がある場合には最後に追加することができます。以下の例では、時間依存性を無視してRLC回路を解析する方法を示しています。

C - 例と詳細な解説

例1
直列RLC回路において、電源電圧が \( v_i = 20 \cos (\omega t) \) で与えられており、ここで \( \omega = 1000 \; rad/s \)、キャパシタの容量 \( C = 200 \; \mu F \)、インダクタのインダクタンス \( L = 400 \; mH \) および抵抗の抵抗値 \( R = 400 \; \Omega \) です。
a) キャパシタ、インダクタ、抵抗のインピーダンスおよびRLC回路のインピーダンス \( Z \) を複素形式で求めなさい。
b) 複素形式での電流とすべての電圧を求めなさい。
c) 実際の電流と電圧を求めなさい。

例1の解答
a)
抵抗 \( R \) の抵抗値 \( Z_R \) の複素形式インピーダンスは次のように表されます。
\( Z_R = R = 400 \; \Omega \)
インダクタンス \( L \) のインダクタ \( Z_L \) の複素形式インピーダンスは、インダクティブリアクタンスとも呼ばれ、次のように表されます。
\( Z_L = j \omega L = j \cdot 1000 \cdot 400 \cdot 10^{-3} = 400 j \; \Omega \)
キャパシタンス \( C \) のキャパシタ \( Z_C \) の複素形式インピーダンスは、キャパシティブリアクタンスとも呼ばれ、次のように表されます。
\( Z_C = - \dfrac{1}{\omega C} j = - \dfrac{1}{1000 \cdot 200 \cdot 10^-6} j = - 5 j \; \Omega \)
\( Z = Z_R + Z_L + Z_C = 400 + 400 j - 5 j = 400 + 395 j \)
b)
\( v_i = 20 cos ( \omega t) \)、したがって電源電圧の極形式は \( V_i = 20 \; \angle \; 0\) です。
上で見たように、電流の極形式は次のように表されます。
\( I = \dfrac{V_i}{Z_R + Z_L + Z_C } \)
既知の量を代入します。
\( I = \dfrac{20 \; \angle \; 0}{400 + 395 j}\)
分母を極形式に書き直します。
\( 400 + 395 j = \sqrt {400^2+395^2} \; \angle \; \arctan\left(\dfrac{395}{400}\right) = 562.16 \; \angle \; 44.64^{\circ} \)
\( I \) を評価します。
\( I = \dfrac{20 \; \angle \; 0}{562.16 \; \angle \; 44.64^{\circ}} = \dfrac{20}{562.16} \; \angle \; 0 - 44.64^{\circ} \)
簡略化します。
\( I = 0.0356 \; \; \angle \; - 44.64^{\circ} \) A
\( V_R = R I = 400 (0.0356 \; \; \angle \; - 44.64^{\circ}) = 14.24 \; V \; \angle \; - 44.64^{\circ}\) V
\( V_L = Z_L I = 400 j (0.0356 \; \; \angle \; - 44.64^{\circ}) = 14.24 \; V \; \angle \; 45.36^{\circ}\) V
\( V_C = Z_C I = - 5 j (0.0356 \; \; \angle \; - 44.64^{\circ}) = 0.18 \; V \; \angle \; -134.6^{\circ}\) V

例2
直列RLC回路において、電源電圧が \( v_i = 10 \cos (\omega t) \) で与えられ、キャパシタンス \( C = 200 \; \mu F \)、インダクタンス \( L = 200 \; mH \) および抵抗 \( R = 500 \; \Omega \) です。
a) インピーダンス \( Z \) の虚部がゼロになる角周波数 \( \omega \) を求めなさい。
b) a) で求めた周波数における電流および電圧を求めなさい。

例2の解答
a)
直列RLC回路において、\( Z = R + j(\omega L - \dfrac{1}{\omega C} ) \) です。
\( Z \) の虚部がゼロであるためには、
\( \omega L - \dfrac{1}{\omega C} = 0 \)
これを解いて \( \omega \) を求めます。
\( \omega^2 L C = 1 \)
\( \omega = \dfrac{1}{\sqrt{L C}} \)
\( L \) と \( C \) の数値を代入します。
\( \omega = \dfrac{1}{ \sqrt{ 200\cdot10^{-3} \cdot 200 \cdot 10^{-6}}} = 158.11 \) rad/s
b)
\( I = \dfrac{V_i}{Z} = \dfrac{10 \; \angle \; 0}{R \; \angle \; 0} = \dfrac{10}{500} \; \angle \; 0 = 0.02 \; \angle\; 0 \)
\( V_R = R I = 500 \cdot 0.02 \; \angle \; 0 = 10 \; \angle\; 0 \)
\( V_C = Z_C I = \dfrac{1}{\omega C} \; \angle \; -90^{\circ} \cdot 0.02 \; \angle\; 0 = \dfrac{1}{\omega C} \cdot 0.02 \; \angle \; -90^{\circ} = \dfrac{1}{158.11 \cdot 200 \cdot 10^{-6}} \cdot 0.02 \; \angle \; -90^{\circ} = 0.6324 \; \angle \; -90^{\circ} \)
\( V_L = Z_L I = \omega L \; \angle \; 90^{\circ} \cdot 0.02 \; \angle\; 0 = \omega L \cdot 0.02 \; \angle \; 90^{\circ} = 158.11 \cdot 200 10^{-3} \cdot 0.02 \; \angle \; 90^{\circ} = 0.6324 \; \angle \; 90^{\circ} \)

例3
直列RLC回路において、電源電圧が \( v_i = V_0 \cos (2 \pi f t) \) で与えられ、ここで \( f \) は周波数、キャパシタの容量 \( C = 47 \; \mu F \)、インダクタのインダクタンス \( L = 100 \; mH \) および抵抗の抵抗値 \( R = 200 \; \Omega \) です。
a) キャパシタ、インダクタ、および抵抗の合成インピーダンス \( Z \) を周波数 \( f \) の関数として求め、極形式 \( Z = |Z| \; \angle \; \theta \) で表しなさい。
b) \( \theta = -60^{\circ} \) となる周波数 \( f \) を求めなさい。

例3の解答
a)
直列RLC回路において、\( Z = R + j(\omega L - \dfrac{1}{\omega C}) \) です。
既知の量を数値で代入します。
\( Z = R + j(\omega L - \dfrac{1}{\omega C}) = 200 + j( \omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}})\)
\( Z = \sqrt {200^2 + ( \omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}})^2} \; \angle \; \arctan \left(\dfrac{\omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}}}{200}\right) \)
b)
\( \arctan \left(\dfrac{\omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}}}{200}\right) = -60^{\circ} \)
\( \dfrac{\omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}}}{200} = \tan (-60^{\circ}) = -1.73205 \)
分母をなくすためにすべての項を \( 200 \) 倍します。
\( \omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}} = -346.41 \)
分母をなくすためにすべての項を \( \omega \cdot 47 \cdot 10^{-6} \) 倍します。
\( 47 \cdot 10^{-7} \omega^2 - 1 = -0.01628127 \omega \)
この2次方程式を解いて正の解を選びます。
\( \omega = 53.23 \) rad/s
\( \omega = 2 \pi f = 60.3682 \)
\( f = \dfrac{60.3682}{2 \pi} = 9.60789 \) Hz

例4
直列RLC回路において、電源電圧が \( v_i = V_0 \cos (2 \pi f t) \) で与えられ、キャパシタンス \( C = 470 \mu \)F、インダクタンス \( L = 50 \)mH、および抵抗 \( R \) です。
a) キャパシタ、インダクタ、および抵抗の合成インピーダンス \( Z \) を周波数 \( f \) の関数として求め、極形式 \( Z = |Z| \; \angle \; \theta \) で表しなさい。
b) \( \theta = 40^{\circ} \) および \( |Z| = 100 \) となる抵抗 \( R \) および周波数 \( f \) を求めなさい。

例4の解答
a)
直列RLC回路において、\( Z = R + j(\omega L - \dfrac{1}{\omega C}) \) です。
\( Z \) を極形式で表します。
\( Z = \sqrt{R^2 + (\omega L - \dfrac{1}{\omega C})^2} \; \angle \; \arctan \left( \dfrac{\omega L - \dfrac{1}{\omega C}}{R} \right) \)
b)
\( \theta = \arctan \left( \dfrac{\omega L - \dfrac{1}{\omega C}}{R} \right) = 40^{\circ} \)
\( \dfrac{\omega L - \dfrac{1}{\omega C}}{R} = \tan 40^{\circ} = 0.83909\)
\( \omega L - \dfrac{1}{\omega C} = 0.83909 R \)
これを \( |Z| \) に代入します。
\( \sqrt{R^2 + (0.83909 R)^2} = 100 \)
\( R \) を解いて求めます。
\( R = 76.6048 \; \Omega \)
\( \omega L - \dfrac{1}{\omega C} = 0.83909 R = 64.27832 \)
\( \omega \) を解いて求めます。
\( \omega = 1317.8557 \) rad/s
\( f = \dfrac{1317.8557}{2\pi} = 209.74324 \) Hz

参考文献およびリンク