AC回路での複素数の使用

目次

複素数がAC（交流）回路での電流と電圧の解析と計算にどのように使用されるか、また抵抗、 コンデンサのインピーダンスとインダクタのインピーダンスが複素数でどのように表されるかをここで説明します。また、複素インピーダンスの使用により、AC回路を数学的にモデル化するためにオームの法則に類似した法則を使用できることも示されます。
複素数を使用してAC回路や他の多くの正弦波現象をモデル化することが適している主な理由は次の2つです:
1) AC信号（および他の多くの正弦波現象）は、大きさと位相で特徴付けられ、それらはそれぞれ、複素数のモジュラスと偏角に非常に似ています。
2) 複素数の基本操作（加算、減算、乗算、除算）は、実行とコンピュータ上でのプログラミングが容易です。
注
1) AC回路での電流を表す記号として\( i \)が使用されるため、ここでは虚数単位として\( j \)を使用します。\( j^2 = -1 \)または\( j = \sqrt{-1} \)として定義されています。
2) 記号\( \Re e\)は複素数の実部を表します。

A - 複素数の実部

標準形式で表される複素数\( Z = a + j b \) は、指数形式で次のように書くことができます
\( \displaystyle Z = r e^{j \theta} \)      ここで \( j^2 = -1 \)
そして、極形式では次のように書くことができます
\( Z = r \angle \theta \)
ここで、\( r = \sqrt{a^2 +b^2} \)は\( Z \)のモジュラスであり、\( \tan \theta = \dfrac{b}{a} \)はその偏角です。
指数形式の複素数の両辺の実部を取り出します。
\( \Re e (r e^{j \theta}) = \Re e (r ( \cos \theta + j \sin \theta )) = \Re e (r \cos \theta + j r \sin \theta ) = r \cos \theta \)
以降では、\( \Re e \)は与えられた複素数の実部を意味します。

B - 一変数複素関数の微分

\( f(t) \)が一変数\( t \)を持つ複素関数であり、次の形式で表されるとします。
\( f(t) = a(t) + j b(t) \)
ここで\( a(t) \)は\( f(t) \)の実部、\( b(t) \)は\( f(t) \)の虚部、\( j = \sqrt {-1}\)は虚数単位です。
\( f'(t) \)を\( t \)に関する\( f(t) \)の一階微分とし、次のように定義します。
\( f'(t) = \lim_{h\to 0} \dfrac{f(t+h) - f(t) }{h} \)
この式に\( f(t+h) \)を\( a(t+h) + j b(t+h) \)で置き換えます。
\( f'(t) = \lim_{h\to 0} \dfrac{ a(t+h) + j b(t+h) - (a(t) + jb(t))}{h} \)
次のように項を分離します。
\( f'(t) = \lim_{h\to 0} \dfrac{ a(t+h) - a(t)}{h} + j \lim_{h\to 0} \dfrac{ j b(t+h) - jb(t))}{h} \)
\( f'(t) = a'(t) + j b'(t) \)
これで、\( f(t) \)の微分の実部が \( f(t) \)の実部の微分に等しいことを示すことが容易になります。
\( \Re e(f'(t)) = a'(t) = (\Re e(f(t))' \)
または
\( \Re e \left ( \dfrac{df(t)}{dt} \right) = \dfrac {d a(t)}{dt} = \dfrac {d \left (\Re e(f(t)) \right)}{dt} \)

C - 一変数複素関数の積分

\( f(t) \)が一変数\( t \)を持つ複素関数であり、次の形式で表されるとします。
\( f(t) = a(t) + j b(t) \)
ここで\( a(t) \)は\( f(t) \)の実部、\( b(t) \)は\( f(t) \)の虚部、\( j = \sqrt {-1}\)は虚数単位です。
\( F(t) \)を不定積分で定義します。
\( \displaystyle F(t) = \int f(t) dt = \int (a(t) + j b(t)) dt = \int a(t) dt + j \int b(t) dt \)
これで、 \( f(t) \)の不定積分の実部が \( f(t) \)の実部の不定積分に等しいことを示すことが容易になります。
\( \displaystyle \Re e \left( \int f(t) dt \right) = \int a(t) dt = \int \left( \Re e f(t) \right) dt \)

これで上記の概念を使用して、複素数を使用して単純なAC回路を解析します。

D - AC電圧源と複素数

以降では、\( v(t) \)が時間\( t \)に応じて変化するAC電圧源であり、次のように与えられるとします。
\( v(t) = V_0 \cos(\omega t) \)
ここで\( V_0 \)はピーク電圧に等しい実数であり、\( \omega = 2 \pi f \)も実数であり、\( f \)は電圧源の周波数です。
複素数を使用すると、\( v(t) \)は次のように書くことができます。
\( v(t) = V_0 \cos(\omega t) = \Re e ( V_0 \cos(\omega t) + j V_0 \sin(\omega t) ) = \Re e (V_0 e^{j\omega t} ) \)

E - AC回路の抵抗

次のように示す単純なAC回路を抵抗で考えてみましょう。\( v(t) \)を次のように与えられるAC電圧源とします。
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
ここで\( V_0 \)と\( \omega \)は実数です。


抵抗\( R \)を通る電流\( i \)と抵抗にかかる電圧\( v(t)_R \)の関係は次のように与えられます。
\( v(t)_R = R i \)
上記の単一ループを使用すると、次のようになります。
\( v(t) = v(t)_R \)
\( v(t) \)は\( v(t) = V_0 \cos(\omega t) \)で与えられます。
したがって、
\( v(t)_R = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
上記を組み合わせて、次のように書きます。
\( R i = \Re e (V_0 e^{j\omega t} ) \)       (I)
\( V_R = V_0 e^{j\omega t} \)とし、上記の(I)を次のように書き直します。
\( R i = \Re e V_R \)
\( R \)は実数であるため、上記を次のように書きます。
\( i = \Re e \left( \dfrac{V_R }{R} \right) \)
\( Z_R \)を抵抗のインピーダンスとして次のように定義します。
\( Z_R = R \)
\( R \)は実数であるため、抵抗のインピーダンス\( Z_R \)は実数です。
電流\( i \)は次のように書くことができます。
\( i = \Re e \left( \dfrac{ V_R } {Z_R} \right) \)
次のように定義します。
\( I = \dfrac{ V_R } {Z_R} \)
上記はDC（直流）回路におけるオームの法則に類似した関係を示しています。複素量\( I \)、\( V_R \)、\( R \)の間の上記の関係は、計算をはるかに容易にします。
これにより、複素インピーダンス、電圧、電流を使用して計算を行い、最終的な答えとして実部を取り出すことで計算が簡略化されます。

F - AC回路のコンデンサ

次のように示す単純なAC回路をコンデンサで考えてみましょう。\( v(t) \)を次のように与えられるAC電圧源とします。
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)

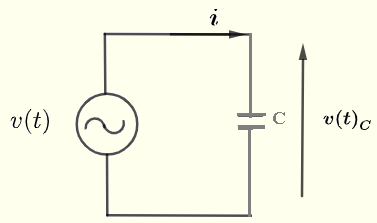
電流\( i \)とコンデンサ\( C \)にかかる電圧\( v(t)_C \)の関係は次のように与えられます。
\( \displaystyle v(t)_C = \dfrac{1}{C} \int i dt \)
上記の単一ループを使用すると、次のようになります。
\( v(t) = v(t)_C \)
次のように与えられる
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
上記を組み合わせて、次のように書きます。
\( \displaystyle \Re e (V_0 e^{j\omega t} ) = \dfrac{1}{C} \int i dt \)
両辺の微分を取ります。
\( \displaystyle \dfrac{d}{dt} (\Re e (V_0 e^{j\omega t}) ) = \dfrac{d}{dt} \left(\dfrac{1}{C} \int i dt \right) \)
上記Bで説明した結果を使用して、次のように書き直します。
\( \displaystyle \Re e \dfrac{d}{dt} \left( V_0 e^{j\omega t} \right) = \dfrac{d}{dt} \left(\dfrac{1}{C} \int i dt \right) \)
簡略化します。
\( \Re e \left( j \omega V_0 e^{j\omega t} \right) = \dfrac{1}{C} i \)
コンデンサの容量\( C \)は実数であるため、次のように書けます。
\( i = \Re e \left( j \omega C \; V_0 e^{j\omega t} \right) \)
\( V_C = V_0 e^{j\omega t} \)とし、コンデンサの複素インピーダンスを次のように定義します。
\( Z_C = \dfrac{1}{j \omega C} = - \dfrac {j} { \omega C} \)
\( C \)は実数であるため、コンデンサのインピーダンス\( Z_C \)は純虚数です。
電流\( i \)は次のように書くことができます。
\( i = \Re e \left( \dfrac{ V_C } {Z_C} \right) \)
次のように定義します。
\( I = \dfrac{ V_C } {Z_C} \)
上記はDC（直流）回路におけるオームの法則に類似しています。複素量\( I \)、\( V_C \)、\( Z_C \)の間の上記の関係は、計算をはるかに容易にします。
これにより、複素インピーダンス、電圧、電流を使用して計算を行い、最終的な答えとして実部を取り出すことで計算が簡略化されます。

G - AC回路のインダクタ

次のように示す単純なAC回路をインダクタで考えてみましょう。\( v(t) \)を次のように与えられるAC電圧源とします。
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)

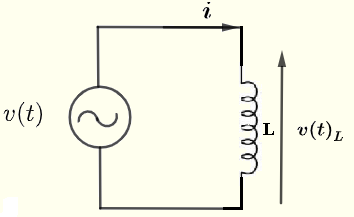
電流\( i \)とインダクタのインダクタンス\( L \)にかかる電圧\( v(t)_L \)の関係は次のように与えられます。
\( v(t)_L = L \dfrac {d i}{ dt} \)
上記の単一ループを使用すると、次のようになります。
\( v(t) = v(t)_L \)
次のように与えられる
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
上記を組み合わせて、次のように書きます。
\( \Re e (V_0 e^{j\omega t} ) = L \dfrac {d i}{ dt} \)
両辺の不定積分を取ります。
\( \displaystyle \int \Re e (V_0 e^{j\omega t}) dt = \int L \dfrac {d i}{ dt} dt \)
上記Cで説明した結果を使用して、次のように書き直します。
\( \displaystyle \Re e \int V_0 e^{j\omega t} dt = \int L \dfrac {d i}{ dt} dt \)
両辺の積分を計算します。
\( \Re e \left( \dfrac{1}{j\omega} V_0 e^{j\omega t} \right) = L i \)
インダクタンス\( L \)は実数であるため、次のように書けます。
\( i = \Re e \left( \dfrac{1}{j \omega L} \; V_0 e^{j\omega t} \right) \)
\( V_L = V_0 e^{j\omega t} \)とし、インダクタのインピーダンス\( Z_L \)を次のように定義します。
\( Z_L = j \omega L \)
\( L \)は実数であるため、インダクタのインピーダンス\( Z_L \)は純虚数です。
電流\( i \)は次のように書くことができます。
\( i = \Re e \left( \dfrac{ V_L } {Z_L} \right) \)
次のように定義します。
\( I = \dfrac{ V_L } {Z_L} \)
上記は複素量\( I \)、\( V_L \)、\( Z_L \)の間の関係をオームの法則に類似して示しています。
これにより、複素インピーダンス、電圧、電流を使用して計算を行い、最終的な答えとして実部を取り出すことで計算が簡略化されます。

H - 結論: 複素インピーダンスを使用したオームの法則

上記で見たように、抵抗、コンデンサ、およびインダクタのインピーダンスは、次のように純実数または純虚数として定義される複素量です。
1) 抵抗\( R\)に対して; インピーダンスは次のように与えられます。\[ Z_R = R \] そして、抵抗\( R \)を通る電流\( I \)（複素形式で）と抵抗\( R \)にかかる電圧\( V_R \)（複素形式で）の関係は、ACにおけるオームの法則であり、次のように与えられます: \[ I = \dfrac{V_R}{Z_R} \] 2) コンデンサ\( C \)に対して; インピーダンスは次のように与えられます。\[ Z_C = -\dfrac{j}{\omega C} \] そして、コンデンサ\( C \)を通る電流\( I \)（複素形式で）とコンデンサ\( C \)にかかる電圧\( V_C \)（複素形式で）の関係は、ACにおけるオームの法則であり、次のように与えられます: \[ I = \dfrac{V_C}{Z_C} \] 3) インダクタ\( L \)に対して; インピーダンスは次のように与えられます。\[ Z_L = j \omega L \] そして、インダクタ\( L \)を通る電流\( I \)（複素形式で）とインダクタ\( L \)にかかる電圧\( V_L \)（複素形式で）の関係は、ACにおけるオームの法則であり、次のように与えられます: \[ I = \dfrac{V_C}{Z_L} \] 私たちは結論として、オームの法則は、抵抗、コンデンサ、およびインダクタのインピーダンスを複素数でモデル化する場合に、AC回路でも有効であると述べました。
また、キルヒホッフの法則も、抵抗、コンデンサ、およびインダクタのインピーダンスを複素数でモデル化する場合、AC回路で有効であることも示されています。
直列および並列のインピーダンスに対する等価インピーダンスは、直列および並列の抵抗に対する類似の規則を使用して計算できます。

E - 解決例

例1
次の条件が与えられた場合、電流\( i \)、抵抗\( R \)にかかる電圧\( v(t)_R \)、およびインダクタ\( L \)にかかる電圧\( v(t)_L \)を\( V_0 \)、\( R \)、\( L \)、および\( \omega \)の式で求めます。
電圧源: \( v(t) = V_0 \cos(\omega t) \) , \( \omega = 2 \pi f \) および \( f \)は周波数です。

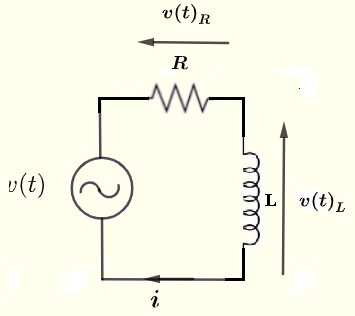
例1の解決
電圧源\( v(t) \)の複素形式を\( V \)とします。
抵抗\( R \)にかかる電圧\( v(t)_R\)の複素形式を\( V_R \)とします。
インダクタ\( L \)にかかる電圧\( v(t)_L\)の複素形式を\( V_L \)とします。
抵抗とコンデンサを通る電流の複素形式を\( I \)とします。
抵抗の複素インピーダンスを\( Z_R = R \)、インダクタの複素インピーダンスを\( Z_L = j \omega L \)とします（上記H部分を参照）。
上記で定義された複素量で回路を再描画し、オームの法則とキルヒホッフの法則を適用します。

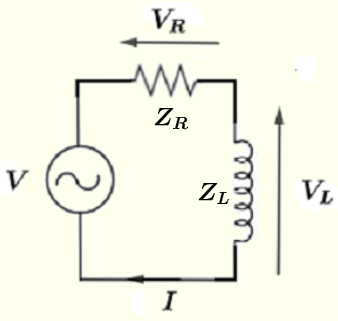
回路を構成するループでキルヒホッフの法則を使用すると、次のようになります。
\( V = V_R + V_L \)         (I)
\( V_R \)および\( V_L \)をオームの法則を使用して次のように書き直します。
\( V_R = Z_R I \)
\( V_L = Z_L I \)
式(I)に代入します。
\( V = Z_R I + Z_L I = R I + j \omega L I = I(R + j \omega L ) \)
上記を\( I \)について解きます。
\( I = \dfrac{V}{R+j \omega L} \)         (II)
分母\( R+j \omega L \)は複素数であり、次のように複素形式で書くことができます。
\( R+j \omega L = r e^{j\theta} \)
ここで、
\( r = |Z| = \sqrt {R^2 + (L\omega)^2} \)はモジュラスであり、
\( \theta = \arctan \left(\dfrac{\omega L}{R} \right) \)は複素平面に示される偏角です。
\( V = V_0 e^{j\omega t} \)とします。
式(II)で\( V \)および\( R+j \omega L \)をそれぞれ複素形式で書き、次のように書きます。
\( I = \dfrac{V_0 e^{j\omega t}}{r e^{j\theta}} \)
指数ルールを使用して、上記を簡略化します。
\( I = \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
オームの法則を使用して次のように書きます。
\( V_R = R I = \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)

\( V_L = Z_L I = \dfrac{j V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
\( V_L \)で\( j \)を指数形式\( j = e^{j \pi/2} \)に書きます。
\( V_L = \dfrac{ e^{j \pi/2} V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
指数ルールを使用して、上記を次のように書き換えます。
\( V_L = \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t + \pi/2 -\theta)} \)
上記で計算された複素量を使用して、次のようにして\( i \)、\( v(t)_R \)、および\( v(t)_L \)を計算します。すなわち、実部を取り出します:
\( i = \Re e I = \Re e \left( \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \right) \)
次のようになります。
\[ i = \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t-\theta) \] \( v(t)_R = \Re e V_R = \Re e \left( \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \right) \) \[ v(t)_R = \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t-\theta) \] \( v(t)_L = \Re e V_L = \Re e \left( \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t + \pi/2 -\theta)} \right) \) \[ v(t)_L = \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t + \pi/2 -\theta) \]

追加の参考資料とリンク