La definizione delle funzioni con molte variabili e il concetto di dominio di queste funzioni sono presentati con esempi.
Sono inclusi anche problemi e le loro soluzioni.
Sono necessarie competenze nella risoluzione di sistemi di disuguaglianze con due variabili per trovare il dominio delle funzioni con due variabili.
Consideriamo alcune formule molto conosciute.
a) Il perimetro \( P \) di un quadrato di lato \( x \) è dato da \( P = 4x\).
b) L'area \( A \) di un rettangolo di lunghezza \( L \) e larghezza \( W \) è data da \( A = LW \)
c) La forza \( F \), secondo la legge di gravitazione universale di Newton, tra due oggetti di masse \( m_1 \) e \( m_2 \) separati da una distanza \( d \) è data da \( F = G \dfrac{m_1 m_2}{d^2} \)
dove \( G \) è una costante.
Si può dire che:
il perimetro \( P \) nella parte a) sopra è una funzione di una variabile \( x \)
l'area \( A \) nella parte b) sopra è una funzione di due variabili \( L \) e \( W \)
la forza \( F \) nella parte c) è una funzione di tre variabili \( m_1 \), \( m_2 \) e \( d \) (Nota che \( G \) è una costante).
Una funzione \( f \) di \( n \) variabili \( x_1, x_2, ..., x_n \), è una regola che assegna un numero reale unico \( f (x_1, x_2, ..., x_n) \) a ogni n-pla di numeri reali \( x_1, x_2, ..., x_n \).
L'insieme \( D \) di tutte le n-ple di numeri reali \( x_1, x_2, ..., x_n \) per le quali la funzione \( f \) è univocamente a valori reali è chiamato dominio della funzione \( f \).
Se consideriamo \( u = f (x_1, x_2, ..., x_n) \), l'insieme di tutti i valori di \( u \) corrispondenti a tutte le n-ple \( x_1, x_2, ..., x_n \) in \( D \) è chiamato intervallo di \( f \) [1] , [2] , [3] .
Esempio 1 Funzione di Due Variabili
Si consideri la funzione \( f \) definita da
\[ f(x,y) = \sqrt{x^2+y^2} + \ln(x-y) \]
a) Calcolare: \( f(4,3) \), \( f(e^2,0) \)
b) Trovare e disegnare il dominio di \( f \)
Soluzione dell'Esempio 1
a)
Per calcolare \( f(4,3) \), dobbiamo sostituire \( x \) con \( 4 \) e \( y \) con \( 3 \)
Quindi
\( f(4,3) = \sqrt{4^2+3^2} + \ln(4-3) \)
Semplifica
\( \quad = \sqrt{25} + \ln(1) = 5 + 0 = 5 \)
Per calcolare \( f(e^2,0) \), dobbiamo sostituire \( x \) con \( e^2 \) e \( y \) con \( 0 \)
Quindi
\( f(e^2,0) = \sqrt{e^2 + 0^2} + \ln(e^2 - 0) \)
Semplifica
\( \quad = e + 2 \)
b)
Il dominio di \( f(x,y) \) è trovato impostando le condizioni:
1) \( \quad x^2+y^2 \ge 0 \), una quantità sotto la radice quadrata deve essere non negativa
2) \( \quad x - y \gt 0 \), l'argomento di un logaritmo deve essere positivo.
La condizione 1) sopra è sempre soddisfatta.
La disuguaglianza nella condizione 2) può essere risolta graficamente per ottenere la soluzione mostrata nel grafico qui sotto.

Esempio 2 Funzione di Tre Variabili
Si consideri la funzione \( g \) definita da
\[ g(x,y,z) = \sqrt{x^2 + y^2 + z^2 - 9} \]
a) Calcolare: \( g(3,-1,1) \), \( g(3/2,1/4,7/2) \)
b) Trovare e descrivere il dominio di \( g \)
Soluzione dell'Esempio 2
a)
Per calcolare \( g(3,-1,1) \), dobbiamo sostituire \( x \) con \( 3 \), \( y \) con \( -1 \) e \( z \) con \( 1 \)
Quindi
\( g(3,-1,1) = \sqrt{3^2 + (-1)^2 + 1^2 - 9} \)
Semplifica
\( \quad = \sqrt{2} \)
Per calcolare \( g(3/2,1/4,7/2) \), dobbiamo sostituire \( x \) con \( 3/2 \), \( y \) con \( 1/4 \) e \( z \) con \( 7/2 \)
Quindi
\( g(3/2,1/4,2) = \sqrt{(3/2)^2 + (1/4)^2 + (7/2)^2 - 9} \)
Semplifica
\( \quad = \dfrac{\sqrt{89}}{4} \)
b)
Il dominio di \( g(x,y,z) \) è trovato impostando le condizioni:
\( x^2 + y^2 + z^2 - 9 \ge 0 \), una quantità sotto la radice quadrata deve essere non negativa
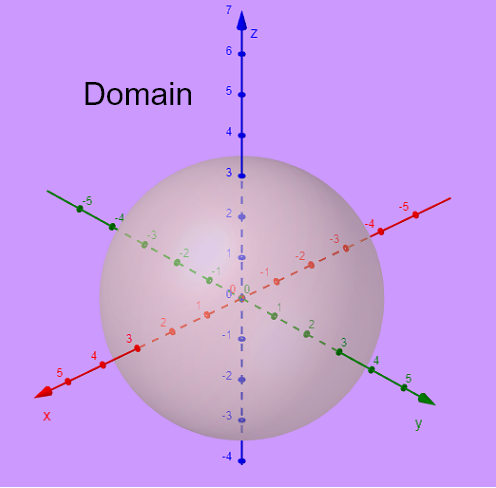
Consideriamo \( x^2 + y^2 + z^2 - 9 = 0 \) che può essere scritto come \( x^2 + y^2 + z^2 = 3^2 \).
Quindi il grafico dell'equazione \( x^2 + y^2 + z^2 - 9 = 0 \) è una sfera di raggio \( 3 \) centrata nell'origine \( (0,0,0) \) come mostrato qui sotto.
Esempio 3 Funzione di Due Variabili
Si consideri la funzione \( h \) definita da
\[ h(x,y) = \dfrac{1}{\ln (1 - x y)} - \sqrt{x - y^2}\]
a) Trovare e descrivere il dominio di \( h \)
b) Fornire esempi di 3 coppie ordinate \( (x,y) \) che si trovano nel dominio di \( h \) e valutare la funzione in questi punti.
c) Fornire esempi di 3 coppie ordinate \( (x,y) \) che NON sono nel dominio.
Soluzione dell'Esempio 3
a)
Il dominio di \( h(x,y) \) è trovato impostando le condizioni:
1) \( \quad 1 - x y \gt 0 \), l'argomento di un logaritmo deve essere positivo
2) \( \quad x - y^2 \ge 0 \), l'argomento della radice quadrata deve essere non negativo.
3) \( \quad \ln (1 - x y) \ne 0 \) o \( 1 - xy \ne 1 \) che è equivalente a \( xy \ne 0 \), il denominatore \( \ln (1 - x y) \) non deve essere uguale a zero.
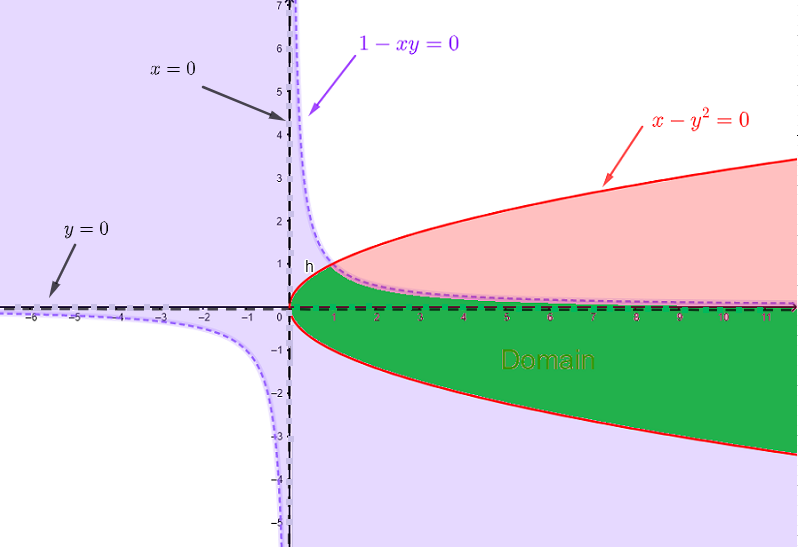
La condizione 1) è risolta graficamente tracciando \( 1 - x y = 0 \) che è equivalente a \( y = \dfrac{1}{x} \) e selezionando l'insieme di soluzione come l'insieme di punti che soddisfano la disuguaglianza \( \quad 1 - x y \gt 0 \). (colore viola chiaro)
La condizione 2) è risolta tracciando \( x - y^2 = 0 \) che è equivalente a \( x = y^2 \), una parabola orizzontale, e selezionando l'insieme di soluzione come l'insieme di punti che soddisfano la disuguaglianza \( \quad x - y^2 \ge 0 \). (colore rosso)
La condizione 3) è soddisfatta da qualsiasi punto che NON si trovi su uno degli assi. (linee tratteggiate sugli assi)
Il dominio è l'intersezione di tutti e tre gli insiemi trovati per le condizioni 1), 2) e 3) e viene mostrato sotto in verde escludendo qualsiasi punto sugli assi \( x \) o \( y \).
Parte A
Date le funzioni:
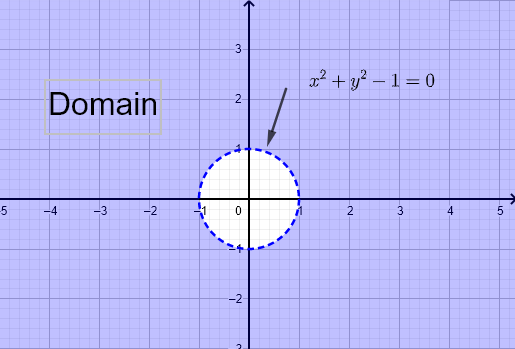
\( f (x,y) = \dfrac{1}{\sqrt{x^2 - y}} \) e \( g (x,y) = \ln (x^2 + y^2 - 1) \)
a) Trovare il dominio di ciascuna funzione
b) Valutare
1) \( f (1,0) \), 2) \( g (1,-1) \), 3) \( \dfrac{f(3,4)}{g(2,0)} \)
Parte B
In un circuito elettrico, la resistenza \( R \) di tre resistori in parallelo e con resistenze \( r_1, r_2, r_3 \) sono correlate da
\( \dfrac{1}{R} = \dfrac{1}{r_1} + \dfrac{1}{r_2} + \dfrac{1}{r_3} \)
a) Esprimere \( R \) come funzione delle variabili \( r_1, r_2, r_3 \).
b) Calcolare \( R \) per \( r_1 = 100 \), \( r_2 = 50 \) e \( r_3 = 20 \).
Parte C
Trovare il dominio delle funzioni
a) \( f(x,y) = \sqrt{x^2+y-2x} \)
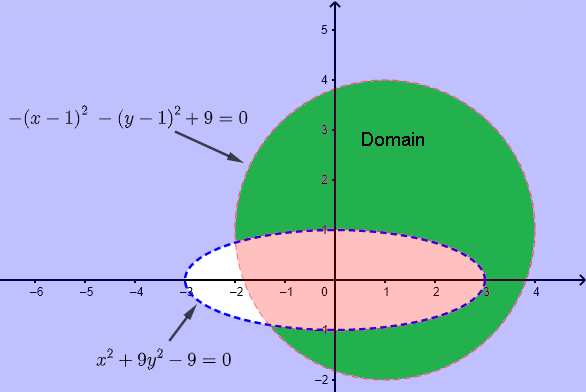
b) \( h(x,y) = \dfrac{\ln(x^2+9 y^2-9)}{\sqrt{7-x^2-y^2+2x+2y}} \)
Parte A
\( f (x,y) = \dfrac{1}{\sqrt{x^2 - y}} \) e \( g (x,y) = \ln (x^2 + y^2 - 1) \)
a)
Il dominio di \( f \) è trovato risolvendo: \( x^2 - y \gt 0 \); il denominatore non deve essere uguale a zero e l'argomento della radice quadrata deve essere non negativo.
Grafica \( y = x^2 \) e seleziona l'area che soddisfa la disuguaglianza \( x^2 - y \gt 0 \). La soluzione grafica è mostrata qui sotto. Il dominio è l'insieme di tutti i punti \( (x,y) \) al di fuori della parabola \( y = x^2 \).

Parte B
a)
Dato \( \dfrac{1}{R} = \dfrac{1}{r_1} + \dfrac{1}{r_2} + \dfrac{1}{r_3} \),
Moltiplica tutti i termini dell'equazione per il prodotto \( r_1 r_2 r_3 \)
\( \dfrac{r_1 r_2 r_3}{R} = \dfrac{r_1 r_2 r_3}{r_1} + \dfrac{r_1 r_2 r_3}{r_2} + \dfrac{r_1 r_2 r_3}{r_3} \)
Semplifica
\( \dfrac{r_1 r_2 r_3}{R} = r_2 r_3 + r_1 r_3 + r_1 r_2 \)
Risolvi per \( R \)
\( R(r_1,r_2,r_3) = \dfrac{r_1 r_2 r_3}{r_2 r_3 + r_1 r_3 + r_1 r_2} \)
b)
\( R(100,50,20) = \dfrac{100 \times 50 \times 20}{50 \times 20 + 100 \times 20 + 100 \times 50} = 12.5\)
Parte C
a) \( f(x,y) = \sqrt{x^2+y-2x} \)
\( f(x,y) \) assume valori reali se l'argomento della radice quadrata è non negativo, quindi la condizione
\( x^2+y-2x \ge 0 \)
Completa il quadrato e riscrivi come
\( (x-1)^2 - 1 + y \ge 0 \)
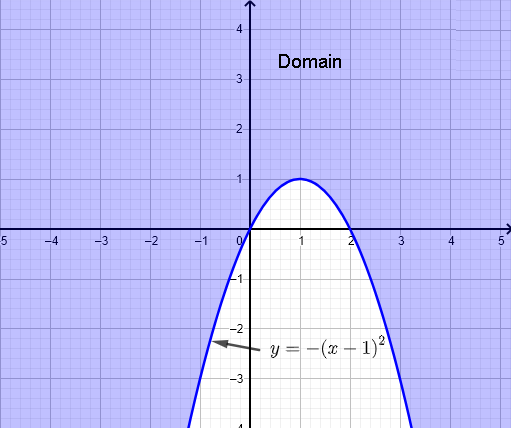
\( y \ge - (x-1)^2 + 1 \)
Grafica la parabola \( y = - (x-1)^2 + 1 \) e identifica il dominio della funzione \( f \).
Il dominio è l'insieme di punti \( (x,y) \) su o fuori dalla parabola \( y = - (x-1)^2 + 1 \) come mostrato nel grafico qui sotto (viola).