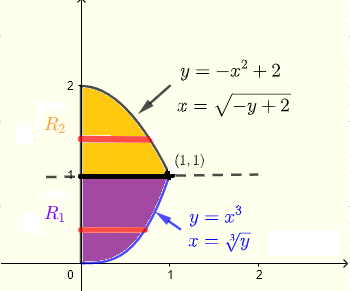Indice
Integrali Doppi su Regioni Generali
Sono presentati esempi per calcolare e valutare integrali doppi su regioni generali insieme alle relative soluzioni dettagliate.
Note Importanti
1) Fare grafici e diagrammi per regioni generali non rettangolari come primo passo rende più facile calcolare integrali doppi con regioni generali.
2) In generale, sono necessari quattro passaggi per calcolare l'integrale doppio su regioni generali di integrazione:
PASSO 1: Fare un grafico e/o un diagramma della regione di integrazione
PASSO 2: Decidere come descrivere la regione generale utilizzando strisce verticali o orizzontali e quindi l'ordine di integrazione
PASSO 3: Descrivere la regione generale di integrazione utilizzando disuguaglianze
PASSO 4: Calcolare l'integrale
3) Di seguito, descriviamo una data regione \( R \) di integrazione come un insieme infinito di strisce verticali che consente di esprimere l'integrale come \( \displaystyle \iint_R f(x,y) \;dy \;dx \) o strisce orizzontali che consente di esprimere l'integrale come \( \displaystyle \iint_R f(x,y) \;dx \;dy \)
\( \)\( \)\( \)
Calcoli di Integrali Doppi su Regioni Generali
Gli obiettivi degli esempi 1 e 2 sono utilizzare grafici e diagrammi per determinare i limiti di integrazione per regioni generali e calcolare l'integrale doppio.
Esempio 1
Domanda: Calcolare l'integrale doppio \( \displaystyle V = \iint_R (x^2+y) \;dy \;dx \) dove la regione \( R \) è un triangolo sul piano \( xy\)-plane delimitato dall'asse \(x\), l'asse \(y\) e la linea \( y = - x + 2 \).
Soluzione dell'Esempio 1
Quattro passaggi principali per calcolare integrali doppi con regioni generali di integrazione.
PASSO 1 Fare un grafico e/o un diagramma che rappresenti la regione generale
Iniziamo disegnando un grafico o/e un diagramma della regione \( R \) di integrazione. In questo esempio è un triangolo con lati sull'asse \(x\) e sull'asse \(y\) e il terzo lato è descritto dall'equazione della linea \( y = - x + 2 \).
Questo triangolo può anche essere definito da tre vertici: l'origine e i punti di intersezione della linea \( y = - x + 2 \) con gli assi \(x\) e \(y\) dati rispettivamente da \( (2,0) \) e \( (0,2) \) come mostrato nel grafico qui sotto.

Ci sono due modi per calcolare l'integrale dato sulla regione data.
PASSO 2 Decidere come descrivere la regione generale utilizzando strisce
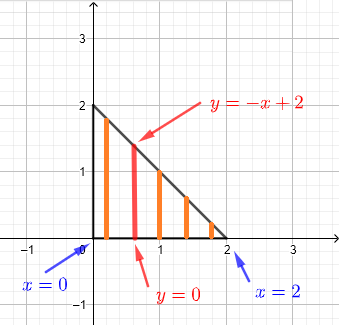
1) Utilizziamo strisce verticali per descrivere la regione \( R \) come mostrato nel grafico qui sotto.
Assumiamo che la regione R possa essere considerata come un insieme infinito di strisce verticali come mostrato nel diagramma qui sotto.
Qualsiasi striscia verticale data, in un dato \( x \), inizia a \( y = 0 \) e termina a \( y = - x + 2 \). Poiché dobbiamo includere tutte le strisce che descrivono la regione \( R \), \( x \) deve assumere valori da \( x = 0 \) a \( x = 2 \). Pertanto, la regione \( R \) di integrazione può essere definita da:
PASSO 3 Descrivere la
regione generale di integrazione utilizzando disuguaglianze
\( R \) : \( 0 \le x \le \ 2 \) , \( 0 \le y \le - x + 2 \)
PASSO 4 Calcolare l'integrale
L'integrale può essere scritto come
\( \displaystyle V = \int_0^2 \int_0^{-x+2} (x^2+y) \;dy \;dx \)
\( = \displaystyle \int_0^2 ( -x^3 +\dfrac{5}{2} x^2 - 2x + 2) \;dx = 8/3\)
Rispondiamo ora alla stessa domanda ma utilizzando strisce orizzontali.
Il PASSO 1 è lo stesso di sopra
PASSO 2 Decidere come descrivere la regione generale utilizzando strisce
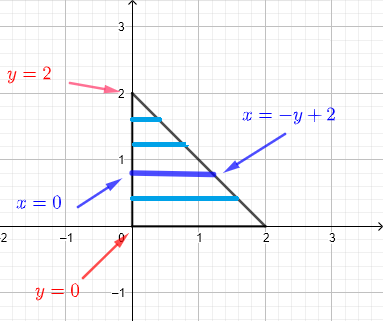
2) Utilizziamo strisce orizzontali per descrivere la regione \( R \) come mostrato nel grafico qui sotto.
Assumiamo che la regione R possa essere considerata come un insieme infinito di strisce orizzontali come mostrato nel diagramma qui sotto.
Qualsiasi striscia verticale data, in un dato \( y \), inizia a \( x = 0 \) e termina a \( x = - y + 2 \). Poiché dobbiamo includere tutte le strisce che descrivono la regione \( R \), \( y \) deve assumere valori da \( y = 0 \) a \( y = 2 \). Pertanto, la regione \( R \) di integrazione può essere definita da:
PASSO 3 Descrivere la regione generale di integrazione utilizzando disuguaglianze
\( R \) : \( 0 \le x \le - y + 2 \) , \( 0 \le y \le 2 \)
PASSO 4 Calcolare l'integrale
Quindi l'integrale può essere scritto come
\( \displaystyle V = \int_0^2 \int_0^{-y+2} (x^2+y) \;dx \;dy \)
\( = \displaystyle \int_0^2 (-\dfrac{1}{3} y^3 + y^2 - 2 y + \dfrac{8}{3} ) \;dy = 8/3 \)
Note In entrambi i casi, l'integrale i cui limiti includono variabili è l'integrale interno
Esempio 2
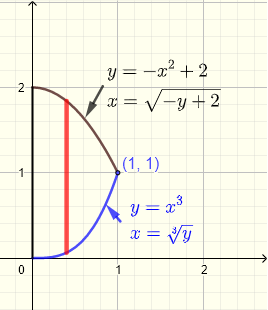
Domanda: Calcolare l'integrale doppio \( \displaystyle V = \iint_R (x+y) \;dy \;dx \) dove la regione \( R \) è sul piano \( xy\)-plane delimitata dall'asse \(y\), dalle curve di equazioni \( y = x^3 \) e \( y = - x^2 + 2 \).
Soluzione dell'Esempio 2
Iniziamo analizzando la regione \( R \) come mostrato nel grafico qui sotto. Le due curve si intersecano in un punto il cui coordinata \( x \) è data dalla soluzione del sistema di equazioni
\( y = x^3 \)
\(y = - x^2 + 2 \)
Un modo per risolvere il sistema sopra è sottrarre le due equazioni e semplificare per eliminare \( y \) e ottenere un'equazione in \(x \) solo per ottenere l'equazione
\( 0 = x^3 + x^2 - 2 \)
Con l'aiuto del grafico, è facile vedere che \( x = 1 \) è una soluzione del sistema di equazioni sopra, che è possibile verificare analiticamente.
La coordinata \(y\) del punto di intersezione delle due curve si trova sostituendo \( x \) con la soluzione trovata in precedenza \( 1 \) in una delle equazioni delle curve per trovare \( y = (1)^3 = 1 \).
Quindi il punto di intersezione è dato da \( (1,1) \)
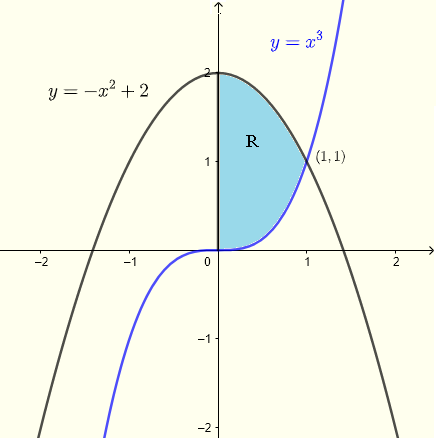
1) Utilizzando strisce verticali
Una data striscia verticale inizia sulla curva \( y = x^3 \) e termina sulla curva \( x = - x^2 + 2 \). Per tutta la regione, \( x \) deve assumere tutti i valori da \( x = 0 \) a \( x = 1 \). Quindi la regione \( R \) di integrazione è data da
\( R \) : \( 0 \le x \le 1 \) , \( x^3 \le y \le - x^2 + 2 \)
Quindi l'integrale può essere calcolato come segue
\( \displaystyle V = \int_0^1 \int_{x^3}^{-x^2+2} (x+y) \;dy \;dx = \dfrac{803}{420}\)
2) Utilizzando strisce orizzontali
Una data striscia orizzontale inizia sull'asse \(y\) \( x = 0 \) e termina sulla curva \( x = \sqrt[3]y \) o sulla curva \( x = \sqrt{- y+ 2} \). A causa delle due curve diverse, la regione \( R \) può essere divisa in due regioni \( R_1 \) e \( R_2 \).
Per la regione \( R_1 \), \( y \) deve assumere tutti i valori da \( y = 0 \) a \( y = 1 \) e per la regione \( R_2 \), \( y \) deve assumere tutti i valori da \( y = 1 \) a \( y = 2 \).
Quindi la regione \( R \) di integrazione ha due parti:
\( R_1 \) : \( 0 \le x \le \sqrt[3]y \) , \( 0 \le y \le 1 \)
e
\( R_2 \) : \( 0 \le x \le \sqrt{- y+ 2} \) , \( 0 \le y \le 1 \)
Quindi l'integrale può essere calcolato come segue
\( \displaystyle V = \iint_{R_1} (x+y) \;dx \;dy + \iint_{R_2} (x+y) \;dx \;dy \)
\( \displaystyle = \int_0^1 \int_{0}^{\sqrt[3]y} (x+y) \;dx \;dy + \int_1^2 \int_{0}^{\sqrt{-y+2}} (x+y) \;dx \;dy = \dfrac{803}{420}\)
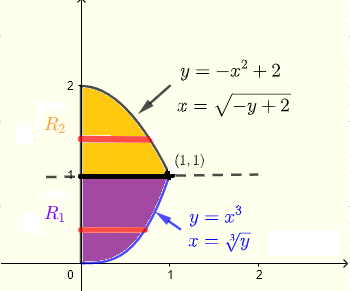
Esempi in cui la Scelta dell'Ordine di Integrazione Dipende dal Problema Dato
Negli esempi 3, 4 e 5, mostriamo che a volte non abbiamo le due scelte dell'ordine di integrazione che di solito abbiamo nelle doppie integrali.
Gli obiettivi degli esempi 3, 4 e 5 consistono nell'utilizzare grafici e diagrammi per determinare l'ordine di integrazione che porta al calcolo analitico dell'integrale doppio.
Esempio 3
Domanda: Calcolare il doppio integrale \( \displaystyle V = \int _0^1 \int _y^1 (y + e^{-x^2}) dx dy \) se possibile. Invertire l'ordine di integrazione se necessario per valutare l'integrale dato.
Soluzione dell'Esempio 3
Iniziamo con l'integrale interno
Sia
\( \displaystyle I = \int _y^1 (y+e^{-x^2}) dx \)
Nel tentativo di valutare \( I \) sopra, l'integrale \( \displaystyle I = \int _y^1 (e^{-x^2}) dx \) non può essere eseguito analiticamente.
Secondo i limiti di integrazione dati, la regione \( R \) di integrazione dell'integrale \( V \) può essere scritta come
\( R \) : \( y \le x \le 1 \) , \( 0 \le y \le 1 \)
con il grafico mostrato di seguito come un insieme di strisce orizzontali.
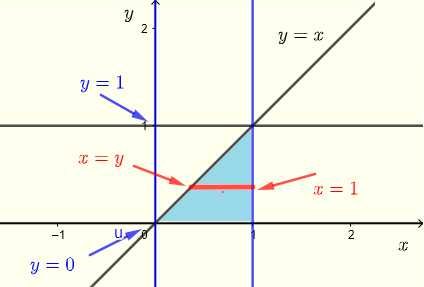
Ora usiamo le strisce verticali per descrivere la regione \( R \) come mostrato nel grafico qui sotto.
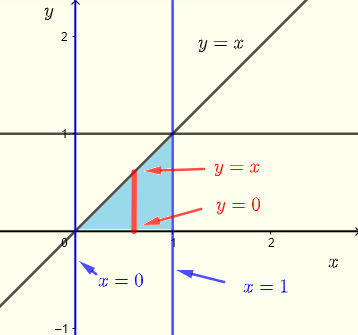
\
Disegna il grafico della regione \( R \) di integrazione per vedere se cambiando l'ordine di integrazione, possiamo procedere ulteriormente.
\( R \) : \( 0 \le x \le 1 \) , \( 0 \le y \le x \)
L'integrale \( V \) può essere scritto come
\( \displaystyle V = \int _0^1 \int _0^x (y + e^{-x^2}) dy dx \)
Valutiamo utilizzando l'integrale interno \( I \) dato da
\( \displaystyle I = \int _0^x (y + e^{-x^2}) dy \)
\( = \left[ \dfrac{y^2}{2} + y e^{-x^2} \right]_0^x \)
\( = \dfrac{x^2}{2} + x e^{-x^2} \)
Ora sostituiamo \( I \) in \( V \) e calcoliamo l'integrale dato
\( \displaystyle V = \int _0^1 (\dfrac{x^2}{2} + x e^{-x^2} ) dx \)
\( = \left[ \frac{x^3}{6}-\frac{1}{2}e^{-x^2} \right]_0^1 \)
\( = \dfrac{2}{3} - \dfrac{1}{2}e^{-1} \)
Esempio 4
Valutare il doppio integrale \( \displaystyle V = \iint_R \left(\sqrt{1+y^3}+\:x\right)\:dy \:dx \) sulla regione \( R \) ombreggiata in blu come mostrato di seguito.
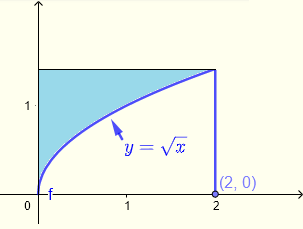
Soluzione dell'Esempio 4
Sia l'integrale interno \( \displaystyle I = \int \left(\sqrt{1+y^3}+\:x\right) \; dy \)
Si può facilmente vedere che questo integrale non è semplice da fare analiticamente.
Scambiamo l'ordine di integrazione.
\( V = \displaystyle \iint_R \left(\sqrt{1+y^3}+\:x\right)\:dx \:dy \)
La regione \( R \) può essere descritta come:
\( R\) : \( 0 \le x \le y^2 \) , \( 0 \le y \le \sqrt 2 \)
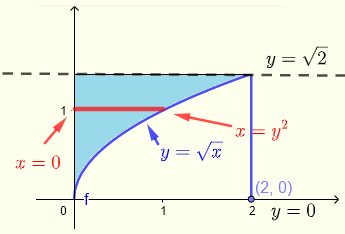
\( \displaystyle V = \int _0^{\sqrt 2} \int _0^{y^2} \left(\sqrt{1+y^3}+\:x\right) dx dy \)
Valutiamo l'integrale interno \( I \).
\( I = \displaystyle \int _0^{y^2} \left(\sqrt{1+y^3}+\:x\right) dx \)
\( = \left [ x \sqrt{1+y^3} + \dfrac{x^2}{2} \right]_0^{y^2} \)
Valutiamo e semplifichiamo
\( = y^2\sqrt{y^3+1}+\frac{y^4}{2} \)
Sostituire \( I \) in \( V \) e calcolare l'integrale esterno
\( \displaystyle V = \int _{0\:}^{\sqrt 2} \left(y^2\sqrt{y^3+1}+\frac{y^4}{2} \right) \; dy \)
Calcolare l'integrale sopra
\( \displaystyle V = \left [ \frac{2}{9}\left(y^3+1\right)^{\frac{3}{2}}+\frac{y^5}{10} \right]_0^{\sqrt 2} \)
Semplificare
\( V = \frac{2}{9}\left(\left(\sqrt{2}\right)^3+1\right)^{\frac{3}{2}}+\frac{\left(\sqrt{2}\right)^5}{10}-\dfrac{2}{9} \approx 2.00 \)
Esempio 5
Valutare il doppio integrale \( \displaystyle V = \iint_R (x+y)\:dydx \) sulla regione \( R \) delimitata dalle curve delle equazioni \( x = (y-2)^2-2 \) e \( y = - x + 6 \)
Soluzione dell'Esempio 5
Se si utilizzano strisce verticali, la regione di integrazione avrà due parti perché i limiti di \( y \) sono diversi negli intervalli \( -2 \le x \le 2 \) e \( 2 \le x \le 7 \) e i calcoli dell'integrale sono molto impegnativi.
Utilizziamo quindi strisce orizzontali.
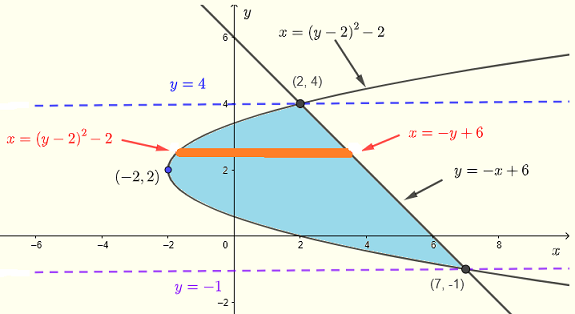
La regione \( R \) può essere descritta come:
\( R\) : \( (y-2)^2 - 2 \le x \le -y+6 \) , \( -1 \le y \le 4 \)
\( \displaystyle V = \int _{-1}^{4} \int _{(y-2)^2 - 2}^{-y+6} (x+y)\:dx \: dy \)
Sia l'integrale interno \( \displaystyle I = \int _{(y-2)^2 - 2}^{-y+6} (x+y)\:dx \)
Calcoliamo il precedente integrale
\( I = \dfrac{-y^4+6y^3-13y^2+12y+32}{2} \)
Sostituire \( I \) in \( V \) e calcolare l'integrale esterno
\( \displaystyle V = \int _{-1}^4 \left( \dfrac{-y^4+6y^3-13y^2+12y+32}{2} \right) \; dy \)
Calcoliamo il precedente integrale
\( \displaystyle V = \dfrac{1}{2} \left[-\dfrac{y^5}{5}+\dfrac{3y^4}{2}-\dfrac{13y^3}{3}+6y^2+32y\right]_{-1}^4 \)
Valutare
\( V = \dfrac{875}{12} \)
Nota
Come esercizio, dimostrare che utilizzando strisce verticali, il doppio integrale è dato da:
\( \displaystyle \int _{-2}^2\:\int _{2-\sqrt{x+2}}^{2+\sqrt{x+2}}\:\left(x+y\right)dydx+\int _2^7\:\int _{2-\sqrt{x+2}}^{-x+6}\:\left(x+y\right)dydx \)
Altre domande con risposte
Parte 1
-
Scrivere i limiti del doppio integrale \( \displaystyle V = \iint_R x y \;dy \;dx \) e \( \displaystyle V = \iint_R x y \;dx \;dy \) dove la regione \( R \) è sul piano \( xy\) tale che \(x \ge 0\) e \(y \ge 0\) e è delimitata dalla curva il cui equazione è data da
\( x^2 + y^2 = 1 \) e valutarlo.
-
Scrivere i limiti del doppio integrale \( \displaystyle V = \iint_R \sin(x^2) \;dy \;dx \) e \( \displaystyle V = \iint_R \sin(x^2) \;dx \;dy \) dove la regione \( R \) è un triangolo con i vertici nei punti \( A(0,0)\) , \( B(3,0) \) e \( C(3,3) \) e valutarlo.
Parte 2
Valutare \( \displaystyle V = \int _0^1 \int _{ \arcsin y}^{\frac{\pi }{2}}\:\left(xy\right)dxdy \)
Risposte alle domande precedenti
Parte 1:
-
Regione di integrazione
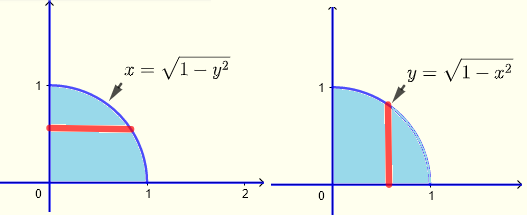
Strisce verticali
\( 0 \le x \le 1 \) , \( 0 \le y \le \sqrt{1-x^2} \)
\( \displaystyle \int _0^1\:\int _0^{\sqrt{1-x^2}}\:xy\:dy\:dx = 1/8 \)
Strisce orizzontali
\( 0 \le x \le \sqrt{1-y^2} \) , \( 0 \le y \le 1 \)
\( \displaystyle \int _0^1\:\int _0^{\sqrt{1-y^2}}\:xy\:dx\:dy = 1/8\)
-
Regione di integrazione

Strisce verticali
\( 0 \le x \le 3\) , \( 0 \le y \le x \)
\( \displaystyle \int _0^3\:\int _0^x \:\sin(x^2)\:dy\:dx = \dfrac{1}{2}\left(-\cos \left(9\right)+1\right) \)
Strisce orizzontali
\( y \le x \le 3 \) , \( 0 \le y \le 3 \)
\( \displaystyle \int _y^3\:\int _0^3\:\sin(x^2)\:dx\:dy \) Molto difficile da risolvere analiticamente.
Parte 2
\( \displaystyle V = \int _0^1 \int _{ \arcsin y}^{\frac{\pi }{2}}\:\left(xy\right)dxdy \)
Calcolare l'integrale interno \( I \) dato da
\( \displaystyle I = \int _{ \arcsin y}^{\frac{\pi }{2}}\:\left(xy\right)dx \)
\( = y \left(\dfrac{\pi^2}{8} - \dfrac{\arcsin^2(y)}{2} \right) \)
Sostituire \( I \) nella sua espressione nell'integrale \( V \)
\( \displaystyle V = \int _0^1 (y \left(\dfrac{\pi^2}{8} - \dfrac{\arcsin^2(y)}{2} \right)) dy \)
che è difficile da fare analiticamente.
Ricominciamo e ora invertiamo l'ordine di integrazione
Iniziamo graficando la regione \( R \) di integrazione
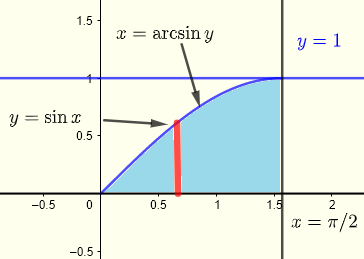
\( \displaystyle V = \int _0^{\frac{\pi }{2}} \int _0^{\sin x} x \; y \; dy \;dx \)
Sia l'integrale interno \( I = \int _0^{\sin x} x \; y \; dy \)
Calcoliamo \( I \)
\( I = x\frac{\sin ^2\left(x\right)}{2} \)
\( \sin^2(x) = \dfrac{1-\cos(2x)}{2} \)
\( I = \dfrac{x}{4}(1-cos(2x) \)
Sostituisci \( I \) in \( V \)
\( \displaystyle V = \int _0^{\frac{\pi }{2}} (\dfrac {x}{4} - \dfrac {x}{4} \cos (2x) ) dx \)
Dividi l'integranda
\( \displaystyle = \int _0^{\frac{\pi }{2}} \dfrac {x}{4} dx
- \int _0^{\frac{\pi }{2}} \dfrac {x}{4} \cos (2x) dx \)
L'integrale a destra è risolto utilizzando la tecnica dell'integrazione per parti per ottenere
\( = \left[ \frac{x^2}{8} \right]_0^{\pi/2}- \left[\frac{1}{8} x \sin (2x)+\frac{1}{16}\cos (2x) \right]_0^{\pi/2} \)
Valuta
\( = \dfrac{\pi^2+4}{32} \)
Altri Riferimenti e Link
- Calcoli di Doppie Integrali
- Howard Anton, Irl C. Bivens, Stephen Davis ; Calcolo: Trascendenti Precoci; Willey, 2012.
- Gilbert Strang; MIT, Calcolo, Wellesley-Cambridge Press, 1991
- Joel Hass, Università della California, Davis; Maurice D. Weir Naval Postgraduate School; George B. Thomas, Jr.Massachusetts Institute of Technology ; Calcolo Universitario , Trascendenti Precoci, Terza Edizione
, Boston Columbus , 2016, Pearson.
Matematica per Ingegneria con Esempi e Soluzioni