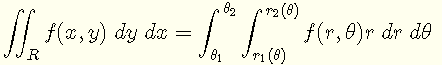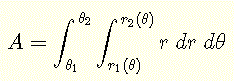Indice
Integrali Doppi in Coordinate Polari
Vengono presentati esempi su come calcolare integrali doppi in coordinate polari e regioni generali di integrazione insieme alle loro soluzioni dettagliate. Gli esempi mostrano anche che convertire gli integrali doppi da coordinate cartesiane a coordinate polari può renderne più semplice la valutazione utilizzando funzioni elementari.
Converti Integrali Doppi in Coordinate Polari
Il cambio di integrali doppi da coordinate cartesiane (o rettangolari) a coordinate polari è dato da [1]
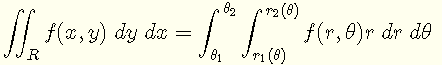
con le relazioni tra le coordinate rettangolari x e y; e le coordinate polari r e θ sono date da [6]
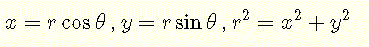
L'area A di una regione chiusa R descritta in coordinate polari è data da
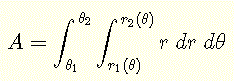
Esempi con Soluzioni Dettagliate
Esempio 1
\( \) \( \) \( \) \( \)
Domanda: Calcolare l'integrale doppio \( \displaystyle V = \iint_R \sqrt {1 - x^2 - y^2} \;dy \;dx \) dove la regione \( R \) è la superficie racchiusa da un cerchio nel piano \( xy \) con centro nell'origine e raggio uguale a \( 1\).
Soluzione all'Esempio 1
L'integrale dato è in coordinate cartesiane e non può essere risolto utilizzando funzioni elementari. Proviamo a convertirlo in coordinate polari.
Sia \( f(x,y) = \sqrt {1 - x^2 - y^2} \) ed esprimiamolo in coordinate polari.
-example-1.gif)
\( r^2 = x^2 + y^2 \)
Quindi la funzione \( f(x,y) \) in forma polare è data da
\( f(r,\theta) = \sqrt {1 - r^2} \)
La regione \( R \) di integrazione è un cerchio e può essere definita dalle disuguaglianze seguenti:
\( R: \) \( 0 \le \theta \le 2\pi \) e \( 0 \le r \le 1 \)
L'integrale dato in coordinate cartesiane può essere convertito in coordinate polari come segue
\( \displaystyle V = \iint_R \sqrt {1 - x^2 - y^2} \;dy \;dx = \int_0^{2\pi} \int_0^{1} \sqrt{1-r^2} \; r \; dr \; d\theta \)
Sia \( I \) l'integrale interno definito da
\( \displaystyle I = \int_0^{1} \sqrt{1-r^2} \; r \; dr \)
\( = \left[ -\frac{1}{3}\left(1-r^2\right)^{\frac{3}{2}} \right]_0^1 = \dfrac{1}{3} \)
Sostituendo \( I \) e calcolando \( V \)
\( \displaystyle V = \int_0^{2\pi} (1/3) \; d\theta \)
\( = \dfrac{1}{3} \left[ \theta \right]_0^{2\pi} \)
\( = \dfrac{2\pi}{3} \)
Esempio 2
Domanda: Calcolare l'integrale doppio \( \displaystyle V = \int_0^{1} \int_0^{\sqrt{1-x^2}} e^{x^2+y^2} \; dy \; dx \)
Soluzione all'Esempio 2
L'integrale dato non può essere facilmente calcolato in coordinate cartesiane, quindi è necessario utilizzare invece le coordinate polari, che potrebbero semplificarne la valutazione.
Esprimiamo \( f(x,y) = e^{x^2+y^2} \) in coordinate polari.
\( r^2 = x^2 + y^2 \)
Quindi la funzione \( f(x,y) \) in forma polare è data da
\( f(r,\theta) = e^{r^2} \)
In coordinate cartesiane, la regione \( R \) di integrazione è definita dai limiti di integrazione dati.
\( R: \) \( 0 \le x \le 1 \) e \( 0 \le y \le \sqrt{1-x^2} \)
Risolviamo l'ineguaglianza \( y \le \sqrt{1-x^2} \) graficamente
Eleviamo al quadrato entrambi i lati dell'ineguaglianza
\( y^2 \le 1-x^2 \)
Riscriviamo con i termini in \( x \) e \( y \) sul lato sinistro
\( y^2 + x^2 \le 1 \)
L'ineguaglianza sopra è l'insieme di tutti i punti \( (x,y) \) all'interno o sul cerchio con centro nell'origine \( (0,0) \) e raggio \( 1 \)
Mettendo insieme tutte le disuguaglianze, la regione di integrazione \( R \) è mostrata di seguito.

La regione sopra in forma polare è mostrata di seguito

ed è definita dalle disuguaglianze
\( R: \) \( 0 \le \theta \le \pi/2 \) e \( 0 \le r \le 1 \)
L'integrale può ora essere convertito in coordinate polari come segue
\( \displaystyle V = \int_0^{1} \int_0^{\sqrt{1-x^2}} e^{x^2+y^2} \; dy \; dx = \int_0^{\pi/2} \int_0^1 e^{r^2} r \; dr \; d\theta \)
Sia \( I \) l'integrale interno definito da
\( \displaystyle I = \int_0^1 e^{r^2} r \; dr \)
\( = \left[ \dfrac{1}{2} e{r^2} \right]_0^1 \)
\( = \dfrac{1}{2} (e - 1) \)
Sostituendo \( I \) in \( V \)
\( \displaystyle V = \int_0^{\pi/2} \dfrac{1}{2} (e - 1) \; d\theta \)
\( = \dfrac{\pi}{4} (e - 1) \)
Esempio 3
Domanda: Esprimere l'integrale \( \displaystyle V = \iint_R {x^2+y^2} \; dy \; dx \) dove \( R \) è un cerchio sul piano \( xy \) con centro nel punto \( (1,0) \) e raggio pari a \( 1 \) usando coordinate cartesiane (o rettangolari) e coordinate polari? Valutare l'integrale.
Soluzione all'Esempio 3
Prima di tutto grafichiamo la regione di integrazione \( R \) e la definiamo in termini di coordinate cartesiane e polari.
1) Coordinate cartesiane
L'equazione del cerchio con centro in \( (1,0) \) e raggio pari a \( 1 \) è data da
\( (x-1)^2 + y^2 = 1 \)
Espandiamo e raggruppiamo termini simili
\( x^2 - 2x + y^2 = 0 \)
Risolviamo l'equazione precedente per \( y \) per ottenere due soluzioni
\( y = \pm \sqrt {2x-x^2} \)
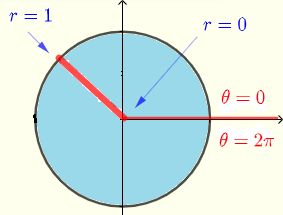
Utilizzando strisce verticali, la regione \( R \) può essere descritta dalle disuguaglianze
\( R: \) \( 0 \le x \le 2 \) e \( - \sqrt {2x-x^2} \le y \le \sqrt {2x-x^2} \)
L'integrale può essere scritto come
\( \displaystyle V = \int_0^2 \int_{-\sqrt {2x-x^2}}^{\sqrt {2x-x^2}} \; \; (x^2+y^2) \; dy \; dx \)
Sia \( I_1 \) l'integrale interno dato da
\( \displaystyle I_1 = \int_{-\sqrt {2x-x^2}}^{\sqrt {2x-x^2}} \; \; (x^2+y^2) \; dy \)
Valutiamo \( I_1 \)
\( \displaystyle I_1 = 2x^2\sqrt{2x-x^2}+2\cdot \frac{\left(2x-x^2\right)^{\frac{3}{2}}}{3} \)
Il prossimo passo per calcolare l'integrale esterno sopra è un passo impegnativo in coordinate cartesiane.
2) Coordinate polari
Utilizzando strisce dall'origine fino a un punto sul cerchio: all'origine \( r = 0 \); sul cerchio \( r = \sqrt {x^2 + y^2} \)
Convertiamo l'equazione del cerchio, \( x^2 + y^2 = 2x \), in forma polare.
Dalla relazione tra le coordinate rettangolari e polari [6], abbiamo
\( r^2 = x^2 + y^2 \) e \( x = r \cos \theta \)
Sostituendo \( x^2 + y^2 \) con \( r^2 \) e \( x \) con \( r \cos \theta \) nell'equazione \( x^2 + y^2 = 2x \) otteniamo
\( r^2 = 2 r \cos \theta \)
Dividiamo entrambi i lati dell'equazione precedente per \( r \)
\( r = 2 \cos \theta \)
In coordinate polari, la regione \( R \) può essere descritta dalle disuguaglianze
\( R: \) \( -\pi/2 \le \theta \le \pi/2 \) e \( 0 \le r \le 2 \cos \theta \)

Utilizziamo \( r^2 = x^2 + y^2 \)
per scrivere l'integrale in forma polare come
\( \displaystyle V = \int_{-\pi/2}^{\pi/2} \int_{0}^{2 \cos \theta} r^2 \; r \; dr \; d\theta \)
Sia \( I \) l'integrale interno definito da
\( \displaystyle I = \int_{0}^{2 \cos \theta} r^2 \; r \; dr \)
Valutiamo
\( \displaystyle I = \left[ r^4 / 4 \right]_{0}^{2 \cos \theta} \)
\( \displaystyle I = 4 cos^4 \theta \) (eq 1)
Riduciamo la potenza nell'espressione precedente \( \cos^4 \theta \)
\( \cos^4 \theta = \cos^2 \theta \cos^2 \theta \)
Usiamo l'identità di riduzione di potenza
\( \cos^2 \theta = \dfrac{cos (2\theta) + 1}{2} \)
Quindi
\( \cos^4 \theta = \left( \dfrac{\cos (2\theta) + 1}{2} \right)^2 \)
\( = \dfrac{\cos^2(2\theta) + 2 \cos (2\theta) + 1}{4} \)
Usiamo l'identità di riduzione di potenza un'altra volta per ottenere
\( \cos^4 \theta = \dfrac{\cos(4\theta) + 4\cos(2\theta) }{8} + 3/8 \)
Ora sostituiamo l'espressione precedente in (eq 1) per ottenere
\( I = \dfrac{\cos(4\theta) + 4\cos(2\theta) }{2} + 3/2 \)
Sostituiamo \( I \) nell'integrale e valutiamo
\( \displaystyle V = \int_{-\pi/2}^{\pi/2} (\dfrac{\cos(4\theta) + 4\cos(2\theta) }{2} + 3/2 ) \; d\theta \)
\( \displaystyle = \left[ \frac{1}{2}\left(\frac{1}{4}\sin \left(4\theta\right)+2\sin \left(2\theta\right)\right)+\frac{3}{2}\theta \right]_{-\pi/2}^{\pi/2} \)
\( = \dfrac{3\pi}{2} \)
L'integrale dato è molto più facile da valutare usando le coordinate polari.
Esempio 4
Domanda: Cambiare l'integrale \( \displaystyle V = \int_{-1}^0 \int_{-\sqrt{1-x^2}}^0 \dfrac{\sqrt{x^2+y^2}}{1+\sqrt{x^2+y^2}} \; dy \; dx \) in coordinate polari e valutarlo.
Soluzione all'Esempio 4
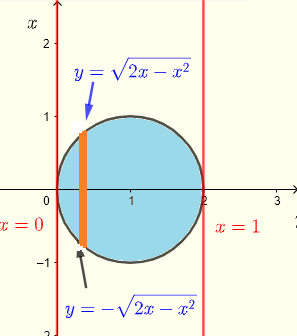
Dai limiti di integrazione nelle coordinate rettangolari, deduciamo la regione \( R \) di integrazione che è un quarto di cerchio nel quadrante III come
\( R: \) \( 0 \le x \le 2 \) e \( - \sqrt {1-x^2} \le y \le 0 \)
e il suo grafico come mostrato di seguito
In coordinate polari usando strisce dall'origine a un punto sul quarto di cerchio: all'origine \( r = 0 \). Sul cerchio \( r = 1 \), la regione \( R \) di integrazione in coordinate polari può essere definita come
\( R: \) \( \pi \le \theta \le 3\pi/2 \) e \( 0 \le r \le 1 \)
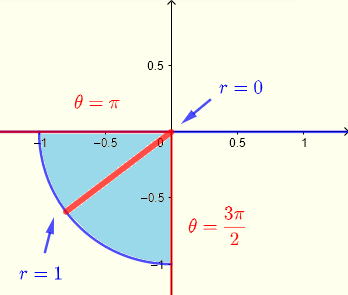
Usiamo \( r = \sqrt { x^2 + y^2 } \)
per scrivere l'integrale dato in forma polare come
\( \displaystyle V = \int_{\pi}^{3\pi/2} \int_{0}^{1} \dfrac{r}{1+r} \; r \; dr \; d\theta \)
\( \displaystyle = \int_{\pi}^{3\pi/2} \int_{0}^{1} \dfrac{r^2}{1+r} \; dr \; d\theta \)
Usiamo la divisione per espandere l'integranda \( \dfrac{r^2}{1+r} \) come segue
\( \dfrac{r^2}{1+r} = r-1+\frac{1}{r+1} \)
Sostituisci l'integranda nella forma espansa nell'integrale
\( \displaystyle V = \int_{\pi}^{3\pi/2} \int_{0}^{1} (r-1+\frac{1}{r+1}) \; dr \; d\theta \)
Integra
\( \displaystyle = \int_{\pi}^{3\pi/2} \left[ \dfrac{r^2}{2} - r + ln |r+1| \right]_0^1 d\theta \)
Valuta
\( \displaystyle = \int_{\pi}^{3\pi/2} (\ln (2)-\dfrac{1}{2}) d\theta \)
Integra
\( = \left( \ln (2)-\dfrac{1}{2} \right) \left[ \; \theta \; \right]_{\pi}^{3\pi/2} \)
Valuta
\( V = \dfrac{\pi}{2} \left( \ln (2)-\dfrac{1}{2} \right) \)
Altre domande con risposte
Parte 1
Converti ciascun integrale in coordinate polari e valutalo.
-
\( \displaystyle V = \int_{-1}^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \; \; \sin(x^2+y^2) \;dy \;dx \)
-
\( \displaystyle V = \int _0^2\:\:\int _0^{\sqrt{4-x^2}} \sqrt{x^2+y^2} \:\;dy\:\;dx\: \)
Parte 2
-
Valuta \( \displaystyle V = \iint_R \: e^{\sqrt{x^2+y^2}} \; dx \; dy \) dove \( R \) è la regione (blu) mostrata nel diagramma qui sotto.
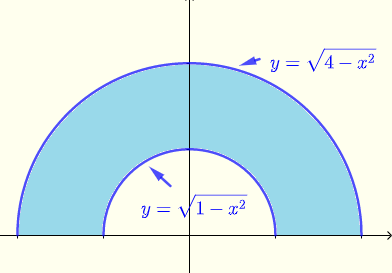
Risposte alle domande sopra
Parte 1:
-
La regione di integrazione in coordinate rettangolari (lato sinistro), data dai limiti di integrazione, e in coordinate polari (lato destro) sono mostrate di seguito.

\( \displaystyle V = \int_{-1}^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \; \; \sin(x^2+y^2) \;dy \;dx \)
Converti l'integrale sopra in coordinate polari
\( \displaystyle V = \int_{0}^{2\pi} \int_0^1 \; \; \sin(r^2) \;r \; dr \;d\theta \)
Valuta
\( = \pi (1 -\cos 1) \)
-
La regione di integrazione in coordinate rettangolari (lato sinistro), data dai limiti di integrazione, e in coordinate polari (lato destro) sono mostrate di seguito.
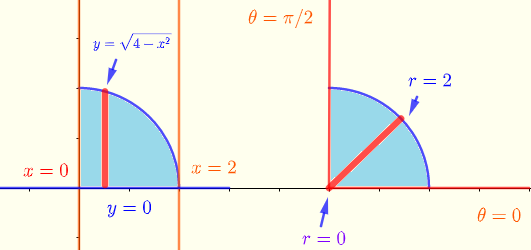
\( \displaystyle V = \int _0^2\:\:\int _0^{\sqrt{4-x^2}} \sqrt{x^2+y^2} \:\;dy\:\;dx\: \)
Converti l'integrale sopra in coordinate polari
\( \displaystyle V = \int_{0}^{\pi/2} \int_0^2 \; \; r^2 \; dr \;d\theta \)
Valuta
\( = \dfrac{4\pi }{3} \)
Part 2
Valuta l'integrale dato usando le coordinate rettangolari
\( \displaystyle V = \int_{-2}^{2} \int_0^{\sqrt{4-x^2}} \: e^{\sqrt{x^2+y^2}} \; dy \; dx - \int_{-1}^{1} \int_0^{\sqrt{1-x^2}} \: e^{\sqrt{x^2+y^2}} \; dy \; dx \)
che è piuttosto impegnativo usando le funzioni elementari.
La regione di integrazione in coordinate polari è mostrata di seguito
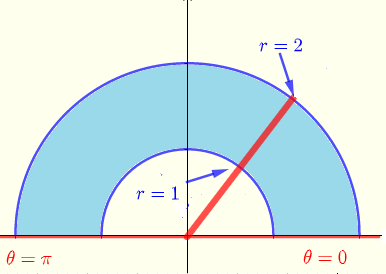
\( R: \) \( 0 \le \theta \le \pi \) and \( 1 \le r \le 2 \)
Dato
\( \displaystyle V = \iint_R \: e^{\sqrt{x^2+y^2}} \; dx \; dy \)
L'integrale dato in coordinate polari è dato da
\( \displaystyle V = \int_0^{\pi} \; \int_1^2 \: r e^{r} \; dr \; d\theta \)
Valuta
\( = \pi e^2 \)
Altre Referenze e Link
- Joel Hass, University of California, Davis; Maurice D. Weir Naval Postgraduate School; George B. Thomas, Jr. Massachusetts Institute of Technology; University Calculus, Early Transcendentals, Terza Edizione, Boston Columbus, 2016, Pearson.
- Calcolo delle Integrali Doppie
Integrali doppie su regioni generali
- Howard Anton, Irl C. Bivens, Stephen Davis; Calcolo: Trascendenti Precoci; Willey, 2012.
- Gilbert Strang; MIT, Calcolo, Wellesley-Cambridge Press, 1991
- coordinate polari
- Converti Coordinate Polari in Coordinate Rettangolari e Viceversa
Matematica per Ingegneri con Esempi e Soluzioni
-example-1.gif)