Viene presentato un calcolatore grafico interattivo online per visualizzare un impulso \( f(t) \) e la sua trasformata di Fourier \( F(\omega) \). \( t \) è il tempo e \( \omega \) è la frequenza angolare.
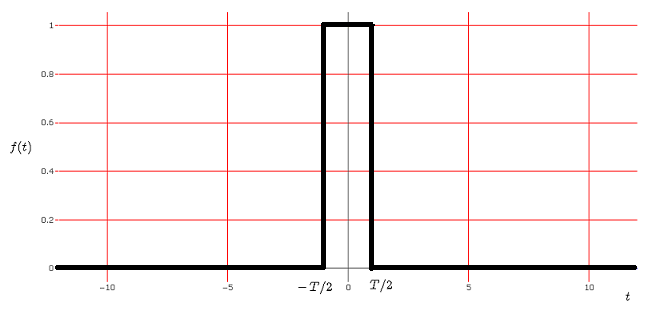La Trasformata di Fourier di \( f(t) \) è definita da
\[ F(\omega) = \int_{-\infty}^{+\infty} f(t) e^\left( - j \omega t\right) dt \\
= \int_{-T/2}^{+T/2} 1 \cdot e^\left( - j \omega t\right) dt \\
= \left[ \dfrac{ e^\left( - j \omega t \right)}{-j \omega} \right]^{T/2}_{-T/2}
\]
Valutare e semplificare per ottenere
\[ F(\omega) = \dfrac{\sin(\omega(T/2))}{\omega/2}
\]
T =