Risolvere i Problemi dei Circuiti in Corrente Alternata con Soluzioni

Indice

La legge di Kirchhoff e la legge di Ohm sono estese e utilizzate per risolvere i problemi dei circuiti in corrente alternata utilizzando impedenze in forme complesse.
Tutte le grandezze come tensioni, correnti e impedenze sono rappresentate da numeri complessi in forma standard e polare .

Riepilogo dei Numeri Complessi

L'unità immaginaria è definita da \( j = \sqrt {-1} \) o \( j^2 = - 1 \)
Un numero complesso \( Z \) nella forma standard \( Z = a + j b \) può essere scritto in forma polare come
\( Z = r \; \angle \; \theta \)
dove \( r \) e \( \theta \) sono il modulo e l'argomento di \( Z \), rispettivamente e sono definiti da
\( r = |Z| = \sqrt {a^2 + b^2} \) e \( \theta = \arctan \left( \dfrac{b}{a} \right) \) all'interno dell'intervallo \( -\pi \lt \theta \le \pi \)
È più semplice dividere o moltiplicare i numeri complessi in forma polare
Sia \( Z_1 = r_1 \; \angle \; \theta_1 \) e \( Z_2 = r_2 \; \angle \; \theta_2 \)
\( Z_1 \cdot Z_2 = r_1 \cdot r_2 \; \angle \; \theta_1 + \theta_2 \)
\( \dfrac{Z_1}{Z_2} = \dfrac{r_1}{r_2} \; \angle \; \theta_1 - \theta_2 \)

Problemi con Soluzioni

Problema 1
Trova la magnitudine e lo sfasamento (forma polare) della corrente attraverso e delle tensioni ai capi del resistore \( R \) e del condensatore \( C \) nel circuito sottostante dato che la sorgente di tensione \( v_i = 10 \cos (\omega t ) \) V, le resistenze \( R = 100 \; \Omega \), \( C = 0.47 \; \mu F \), frequenza \( f = 1 \) kHz e \( \omega = 2 \pi f \).

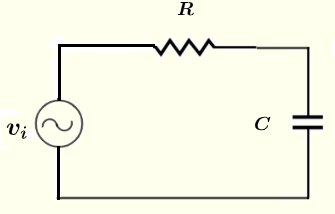
Soluzione al Problema 1
Siano \( V_i \), \( V_R \) \( V_C \) e \( I \) le forme complesse di \( v_i \), \( v_R \) \( v_C \) e \( i \) rispettivamente.


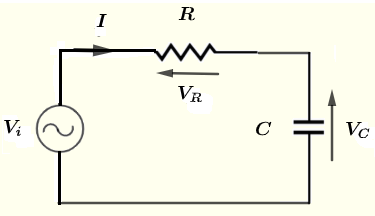
Usa la legge di Kirchhoff della tensione intorno al circuito per scrivere l'equazione
\( V_i - V_R - V_C = 0 \) e la legge di Ohm per una resistenza e la reattanza di un condensatore
\( V_R = R \cdot I \)
\( V_C = X_C \cdot I \)
dove \( X_C = \dfrac{1}{j \omega C} \)
Sostituisci \( V_R \) e \( V_C \) con le loro es pressioni nell'equazione (1)
\( V_i - Z_R I - Z_C I = 0 \) Risolvere il sopra per \( I \) \( I = \dfrac{V_i}{Z_R + Z_C} \) Calcola \( V_R \) e \( V_C \) usando la legge di Ohm come segue \( V_R = Z_R I = \dfrac{V_i Z_R }{Z_R + Z_C} \) \( V_C = Z_C I = \dfrac{V_i Z_C }{Z_R + Z_C} \) In forma polare complessa \( v_i = 10 \cos (\omega t ) \) può essere scritto come \( V_i = 10 \; \angle \; 0 \) Sostituisci ora \( V_i \), \( Z_R \) e \( Z_C \) con le loro espressioni sopra per ottenere \( I = \dfrac{10 \; \angle \; 0}{R - j \dfrac{1}{\omega C}} \) \( V_R = \dfrac{10 R \; \angle \; 0 \; }{R - j \dfrac{1}{\omega C}} \) \( V_C = \dfrac{ (10 \; \angle \; 0 \;) (- j \dfrac{1}{\omega C}) }{R - j \dfrac{1}{\omega C}} \) Fai in modo che il denominatore sia \( Z_D = R - j \dfrac{1}{\omega C} \) e riscrivilo in forma complessa Modulo di \( Z_D \) : \( | Z_D | = \sqrt {R^2 + \dfrac{1}{\omega^2 C^2}} \) Argomento di \( Z_D \) : \( \phi = \arctan \dfrac{-\dfrac{1}{\omega C}}{R} = \arctan \dfrac{-1}{R \omega C} \) Riscrivi ora la quantità complessa \( - j \dfrac{1}{\omega C} \) in forma polare \( - j \dfrac{1}{\omega C} = \dfrac{1}{\omega C} \; \angle \; -\dfrac{\pi}{2} \) Sostituisci ora tutte le quantità complesse in \( I \), \( V_R \) e \( V_C \) con la loro forma polare e riscrivi \( I = \dfrac{10 \; \angle \; 0}{{ | Z_D | \; \angle \; \phi}} \) \( V_R = \dfrac{10 R \; \angle \; 0 \; }{ | Z_D | \; \angle \; \phi} \) \( V_C = \dfrac{10 \; \angle \; 0 \; (\dfrac{1}{\omega C} \; \angle \; -\dfrac{\pi}{2}) }{{ | Z_D | \; \angle \; \phi}} \) Semplifica il sopra \( I = \dfrac{10} { | Z_D | } \; \angle \; - \phi \) \( V_R = \dfrac{10 R}{ | Z_D |} \; \angle \; - \phi \) \( V_C = \dfrac{10}{ \omega C | Z_D | } \; \angle \; -\dfrac{\pi}{2}- \phi \) Ora sostituisci tutte le quantità note con i loro valori numerici \( \omega = 2 \cdot \pi \cdot f = 2 \cdot \pi 10^3 = 2000 \pi \) \( | Z_D | = \sqrt {R^2 + \dfrac{1}{\omega^2 C^2}} = \sqrt {100^2 + \dfrac{1}{(2000 \pi)^2 (0.47 \cdot 10^{-6})^2}} = 353.08 \; \Omega \) \( \phi = \arctan \dfrac{-\dfrac{1}{\omega C}}{R} = \arctan \dfrac{-\dfrac{1}{2000 \pi \cdot 0.47 \cdot 10^{-6} }}{100} = -73.55^{\circ} \) Quindi \( I = \dfrac{10} { | Z_D | } \; \angle \; - \phi = 0.0283 \; \angle \; 73.55^{\circ} \) La magnitudine di \( I \) è \( 0.02832 \; A\) e lo sfasamento è \( 73.55^{\circ} \) \( V_R = \dfrac{10 R}{ | Z_D |} \; \angle \; - \phi = 2.832 \; \angle \; 73.55^{\circ} \) La magnitudine di \( V_R \) è \( 2.832 \; V\) e lo sfasamento è \( 73.55^{\circ} \) \( V_C = \dfrac{10}{ \omega C | Z_D | } \; \angle \; -\dfrac{\pi}{2}- \phi = 9.591 \; \angle \; -16.45^{\circ} \) La magnitudine di \( V_C \) è \( 9.591 \; V\) e lo sfasamento è \( -16.45^{\circ} \)

Problema 2

Trova la magnitudine e lo sfasamento (forma polare) della tensione \( v_o \) nel circuito sottostante dato che la sorgente di tensione \( v_i = 10 \cos (\omega t ) \; V \), le resistenze \( R = 100 \; \Omega \), \( C = 0.47 \; \mu F \), \( L = 300 \; mH \) e la frequenza \( f = 2 \) kHz con \( \omega = 2 \pi f \).


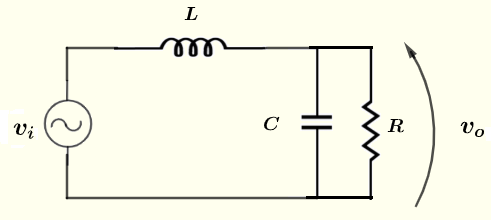
Soluzione al Problema 2
Siano \( I \), \( V_i \) e \( V_0 \) le forme complesse di \( i \), \( v_i \) e \( v_o \) rispettivamente.
\( V_i \) può essere scritto in forma polare come segue
\( V_i = 10 \; \angle \; 0 \)
Le impedenze del resistore \( R \) sono date da
\( Z_R = R \; \)
Le impedenze del condensatore \( C \) sono date da
\( Z_C = - j \dfrac{1}{\omega C} \; \)
Il resistore \( R \) e il condensatore \( C \) sono in parallelo. L'impedenza \( Z \) equivalente a \( R \) e \( C \) è data da

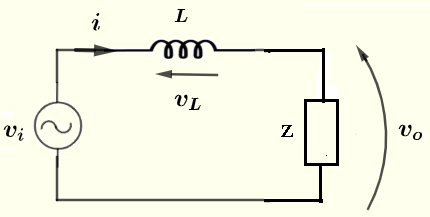
\( Z = \dfrac{Z_R \cdot Z_C}{Z_R + Z_C} \)
L'induttore \( L \) ha impedenza complessa \( Z_L \) data da
\( Z_L = j \omega L \)
Usa la legge di Kirchhoff della tensione intorno al circuito per scrivere l'equazione
\( V_i - V_L - V_0 = 0\)      (1)
Usa la legge di Ohm per scrivere
\( V_L = Z_L I \) e \( V_0 = Z I \)
Sostituisci \( V_L \) e \( V_0 \) con le loro espressioni nell'equazione (1)
\( V_i - Z_L I - Z I = 0 \)
Risolvi per \( I \)
\( I = \dfrac{V_i}{ Z_L + Z} \)
Usa la legge di Ohm per scrivere
\( V_o = Z I = \dfrac{Z}{ Z_L + Z} V_i\)
Sostituisci le quantità conosciute per trovare i valori numerici
\( \omega = 2 \pi f = 2 \pi \cdot 2000 = 4000 \pi \)
\( Z_R = R = 100 \)
\( Z_C = - j \dfrac{1}{\omega C} = - j \dfrac{1}{4000 \pi \cdot 0.47 \cdot 10^{-6}} = - 169.314 j \)

\( Z = \dfrac{R \cdot Z_C}{R + Z_C} \) ( (\( R \) e \( C \) in parallelo )

\( = \dfrac{100 \cdot (- 169.314 j)}{100 - 169.314 j } = 74.138 -43.787 j\)
e
\( Z_L = j \omega L = 4000 \pi \cdot 300 \cdot 10^{-3} j = 3769.911 j \)
\( V_o = \dfrac{Z}{ Z_L + Z} V_i \)

\( = \dfrac{Z}{ Z_L + Z} V_i \)

\( = \dfrac{74.138 -43.787 j}{ 3769.911 j + 74.138 -43.787 j} V_i \)
Semplifica
\( = (-0.01135 -0.02012 j) V_i \)
Scrivi il numero complesso \( (-0.01135 -0.02012 j) \) in forma polare e sostituisci \(V_i \) con i suoi valori in forma polare sopra.
\( = ( 0.02310 \angle -119.43^{\circ} ) (10 \; \angle \; 0) \)
Semplifica
\( V_o = 0.23 \; \angle \; -119.43^{\circ} \)

Problema 3

Trova la magnitudine e lo sfasamento (forma polare) della tensione \( v_o \) nel circuito sottostante dato che la sorgente di tensione \( v_i = 10 \cos (\omega t ) \; V \), le resistenze \( R_1 = 220 \; \Omega \), \( R_2 = 2.2 \; k\Omega \), \( R_3 = 1 \; k\Omega \), \( C_1 = 0.47 \; \mu F \), \( C_2 = 1.5 \; \mu F \), \( L = 30\; mH \) e la frequenza \( f = 2.5 \) kHz con \( \omega = 2 \pi f \).

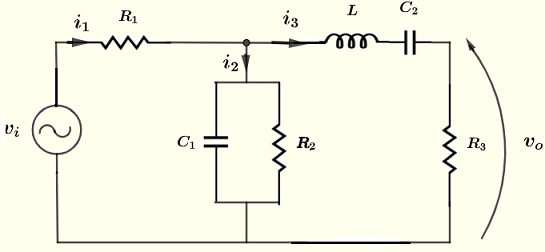
Soluzione all'Esempio 3
Siano \( I_1 \), \( I_2 \), \( I_3 \), \( V_i \) e \( V_0 \) le forme complesse di \( i_1 \), \( i_2 \), \( i_3 \), \( v_i \) e \( v_o \) rispettivamente.
\( V_i \) può essere scritto in forma polare come segue
\( V_i = 10 \; \angle \; 0 \)
\( V_o \) può essere calcolato usando la legge di Ohm
\( V_o = R_3 I_3\)
Quindi dobbiamo calcolare \( I_3 \)
Raggruppiamo le impedenze, come mostrato nel circuito sotto, in modo tale che
\( Z_1 = R_1 \)
\( Z_2 = \dfrac{R_2 ( - \dfrac{1}{\omega C_1} j)}{R_2 - \dfrac{1}{\omega C_1} j} \)      ( \( C_1 \) e \( R_2 \) sono in parallelo)
\( z_3 = R_3 + j \omega L - \dfrac{1}{ \omega C_2} j \)      ( \( C_2 \), \( L \) e \( R_3 \) sono in serie)

La legge di Kirchhoff della tensione applicata ai due circuiti chiusi fornisce 2 equazioni
\( V_i - V_{z_1} - V_{z_2} = 0 \)
\( V_{z_2} - V_{z_3} = 0 \)
Applica la legge di Ohm per scrivere \( V_{z_1} = Z_1 I_1 \), \( V_{z_2} = Z_2 I_2 \) e \( V_{z_3} = Z_3 I_3 \) e sostituisci nelle equazioni sopra per ottenere equazioni che includono solo correnti.
\( V_i - Z_1 I_1 - Z_2 I_2 = 0 \)     (1)
\( Z_2 I_2 - Z_3 I_3 = 0 \)     (2)
Usiamo quindi la legge di Kirchhoff della corrente al nodo A per scrivere
\( I_1 = I_2 + I_3 \)     (3)
Abbiamo 3 equazioni con tre incognite \( I_1 \), \( I_2 \) , e \( I_3 \), ma ne abbiamo bisogno solo di \(I_3\).
Usa l'equazione (3) per sostituire \( I_1 \) nell'equazione (1) con \( I_2 + I_3 \) ed eliminare \( I_1 \) dalle equazioni ottenendo un sistema di due equazioni e due incognite.
\( V_i - Z_1 ( I_2 + I_3) - Z_2 I_2 = 0 \)     (4)
\( Z_2 I_2 - Z_3 I_3 = 0 \)     (5)
Riscrivi il sistema di equazioni nella forma standard
\( (Z_1 + Z_2 ) I_2 + Z_1 I_3 = V_i \)     (4)
\( Z_2 I_2 - Z_3 I_3 = 0 \)     (5)
Usa il determinante per risolvere il sistema di equazioni sopra
\( I_3 = \dfrac{\begin{vmatrix} Z_1 + Z_2 & V_i \\ Z_2 & 0 \end{vmatrix}}{\begin{vmatrix} Z_1 + Z_2 & + Z_1 \\ Z_2 & -Z_3 \end{vmatrix}} \)
Valuta i determinanti per trovare
\( I_3 = \dfrac{Z_2}{(Z_1+Z_2)Z_3 + Z_1 Z_2} V_i \)

Calcoli Numerici
\( \omega = 2 \pi f = 5000 \pi \)
\( Z_1 = 220 \)
\( Z_2 = \dfrac{2200 ( - \dfrac{1}{5000 \pi \cdot 0.47 10^{-6}} j)}{2200 - \dfrac{1}{5000 \pi \cdot 0.47 10^{-6}} j} \)

\( Z_2 = 8.30804 -134.93950 j \)

\( z_3 = 1000 + 5000 \pi \cdot 30 \cdot 10^{-3} j - \dfrac{1}{ 5000 \pi \cdot 1.5 \cdot 10^{-6}} j \)
\( Z_3 = 1000 + 428.79757 j \)
\( I_3 = (0.00013 - 0.00043 j)V_i = 0.00044 \angle -73.18^{\circ} \cdot 10 \angle 0\)
\( V_0 = R_3 I_3 = 1000 \cdot 0.00044 \angle -73.18^{\circ} \cdot 10 \angle 0 \)
Semplifica
\( V_0 = 4.4 \angle -73.18^{\circ} V \)

Altri Problemi con Soluzioni

Problema 4
Dato \( v_i = 10 \angle 0^{\circ} \) , \( R = 200 \; \Omega \), \( C = 0.47 \; \mu F \), \( L = 40 \; mH \) , frequenza \( f = 1 \) kHz.
Trova la corrente \( I \) e la tensione \( V_0 \) attraverso e attraverso l'induttore nelle forme complesse.

Risposta al Problema 4

Risposta: \( I = 0.047 \angle -47.84^{\circ}\) , \(V_0 = 11.38 \angle 42.16^{\circ} \)

Problema 5
Dato \( v_i = 10 \angle 0^{\circ} \) , \( R_1 = 100 \; \Omega \), \( C = 0.47 \; \mu F \), \( R_2 = 120 \; \Omega \), \( R_3 = 200 \; \Omega \), \( R_4 = 400 \; \Omega \), \( L = 20 \; mH \) , frequenza \( f = 2 \) kHz.
Trova le correnti \( I_1 \), \( I_2 \) , \( I_3 \) e le tensioni attraverso ciascuna resistenza nelle forme complesse.

Risposta al Problema 5
Risposte
Correnti: \( I_1 = 0.054 \angle 10.55^{\circ} \; , \; I_2 = 0.048 \angle 23.01^{\circ} \; , \; I_3 = 0.013 \angle -42.22^{\circ} \)
Tensioni: \( V_{R_1} = 5.49 \angle 10.55^{\circ} \; , \; V_{R_2} = 4.71 \angle -12.32^{\circ} \; , \; V_{R_3} = 2.60 \angle -42.22^{\circ} \; , \; V_{R_4} = 2.77 \angle 15.63^{\circ} \)

Altri Riferimenti e Link