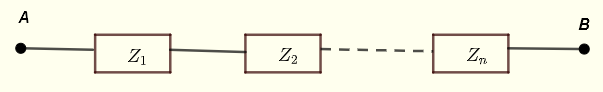
L'impedenza equivalente tra i punti A e B è data da
\[ Z_{AB} = Z_1 + Z_2 + ... + Z_n\]
Qui viene discusso come le impedenze complesse vengono utilizzate per calcolare le impedenze equivalenti alle impedenze in serie e parallelo nei circuiti in corrente alternata. Tutti i passaggi vengono mostrati utilizzando calcoli simbolici e quindi vengono utilizzati valori numerici.
Poiché il simbolo \( i \) è usato per le correnti nei circuiti in corrente alternata, qui usiamo \( j \) come unità immaginaria definita da \( j^2 = -1 \) o \( j = \sqrt{-1} \)
Siano \( Z_1 \), \( Z_2 \), ... \( Z_n \) impedenze in serie come mostrato di seguito.
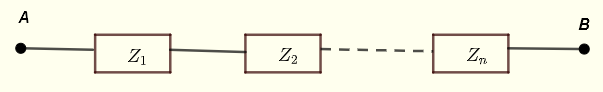
L'impedenza equivalente tra i punti A e B è data da
\[ Z_{AB} = Z_1 + Z_2 + ... + Z_n\]
Esempio 1
Trova l'impedenza complessa equivalente al circuito RLC in serie mostrato di seguito dato:
Frequenza \( f = 1 \; kHz \), \( C = 10 \; \mu F \), \( L = 10 \; mH \) e \( R = 100 \; \Omega \)

Soluzione dei Problemi 1
Sia
\( Z_R = R \), \( Z_C = \dfrac{1}{j \omega C} = \dfrac{-j}{\omega C} \), \( Z_L = j \omega L\)
Applica la regola delle impedenze di un circuito in serie
\( Z_{AB} = Z_R + Z_C + Z_L = R - \dfrac{j}{\omega C} + j \omega L \)
Sia
\( X_L = \omega L = 2 \pi f L \) e \( X_C = \dfrac{1}{\omega C} = \dfrac{1}{2 \pi f C} \)
e riscrivi \( Z_{AB} \) come segue
\( Z_{AB} = R + j(X_L - X_C) \)
Sostituisci con i valori numerici
\( X_L = \omega L = 2 \pi f L = 2 \pi 10^3 10^{-2} = 62.83 \Omega \)
\( X_C = \dfrac{1}{\omega C} = \dfrac{1}{2 \pi f C} = \dfrac{1}{2 \pi 10^3 10^{-5} } = 15.92 \Omega \)
Raggruppa i termini immaginari
\( Z_{AB} = 100 + j ( 62.83 - 15.92 ) \)
Semplifica
\( Z_{AB} = 100 + j ( 62.83 - 15.92 ) = 100 + 46.91 j\)
Scrivi quanto sopra in forma esponenziale
\( Z_{AB} = \sqrt {100^2 + 46.91^2} e^{j \arctan{\dfrac{46.91}{100}}} = 110.45 e^{j 0.44} \)
\( Z_{AB} \) scritto in forma fasoriale
\( Z_{AB} = 110.45 \angle 0.44 \; rad = 110.45 \angle 25.13^{\circ} \)
Un calcolatore di impedenza per circuiti RLC in serie può essere utilizzato per ulteriori esercitazioni.
Siano \( Z_1 \), \( Z_2 \), ... \( Z_n \) impedenze in parallelo come mostrato di seguito.
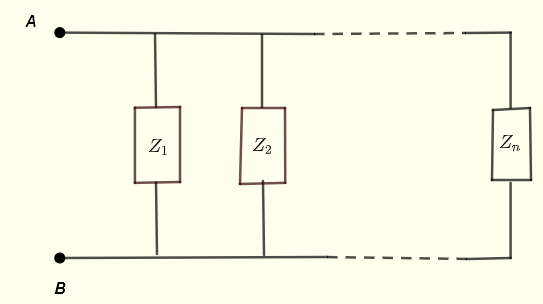
L'impedenza equivalente tra i punti A e B è data da
\[ \dfrac{1
}{Z_{AB}} = \dfrac{1}{Z_1} + \dfrac{1}{Z_2} + ... + \dfrac{1}{Z_n} \]
Esempio 2
Trova l'impedenza complessa equivalente al circuito RLC in parallelo mostrato di seguito dato:
Frequenza \( f = 1.5 \; kHz \), \( C = 15 \; \mu F \), \( L = 20 \; mH \) e \( R = 50 \; \Omega \)

Soluzione dei Problemi 2
Sia
\( Z_R = R \), \( Z_C = \dfrac{1}{j \omega C} \), \( Z_L = j \omega L\)
Applica la regola delle impedenze di un circuito in parallelo
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{Z_R} + \dfrac{1}{Z_C} + \dfrac{1}{Z_L} \)
\( = \dfrac{1}{R} + \dfrac{1}{\dfrac{1}{j \omega C}} + \dfrac{1}{j \omega L} \)
Sia
\( X_L = \omega L \) e \( X_C = \dfrac{1}{\omega C} \)
e riscrivi quanto sopra come
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{R} + \dfrac{1}{\dfrac{X_C}{j}} + \dfrac{1}{j X_L} \)
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{R} + \dfrac{j}{{X_C}} - j \dfrac{1}{ X_L} \)
\( = \dfrac{1}{R} + j (\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} ) \)
Il modulo \( r \) del numero complesso sopra è dato da
\( r = \sqrt { (\dfrac{1}{R})^2 + (\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} )^2} \)
e il suo argomento \( \alpha \) è dato da
\( \alpha = \arctan \left(\dfrac{\dfrac{1}{{X_C}} - \dfrac{1}{ X_L}}{\dfrac{1}{R}} \right) \)
\( = \arctan \left(\dfrac{R}{X_C}-\dfrac{R}{X_L} \right) \)
Ora utilizziamo la forma esponenziale del numero complesso per scrivere
\( \dfrac{1}{Z_{AB}} = r e^{j\alpha} \)
Scriviamo ora l'impedenza equivalente \( Z_{AB} \) come un numero complesso in forma esponenziale
\( Z_{AB} = \dfrac{1}{r} e^{-j \alpha} \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} e^{-j \arctan \left(\dfrac{R}{X_C}-\dfrac{R}{X_L} \right) } \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} e^{j \arctan \left(\dfrac{R}{X_L}-\dfrac{R}{X_C} \right) } \)
Ora utilizziamo i valori dati
\( f = 1.5 \; kHz \), \( C = 15 \; \mu F \), \( L = 20 \; mH \) e \( R = 50 \; \Omega \)
\( X_L = \omega L = 2 \pi f L = 2 \pi 1.5 \times 10^3 \times 20 10^{-3 } = 188.50 \)
\( X_C = \dfrac{1}{\omega C} = \dfrac{1}{ 2\pi f C} = \dfrac{1}{ 2\pi 1.5 \times 10^3 \times 15 10^{-6}} = 7.07\)
Modulo: \( \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{50}\right)^2 + \left(\dfrac{1}{{7.07}} - \dfrac{1}{ 188.50} \right)^2}} \)
\( = 7.27 \)
Argomento: \( \arctan \left(\dfrac{R}{X_L}-\dfrac{R}{X_C} \right) \)
\( = \arctan \left(\dfrac{50}{188.50}-\dfrac{50}{7.07} \right) \)
\( = - 81.64^{\circ} \)
Un calcolatore di impedenza per circuiti RLC in parallelo può essere utilizzato per ulteriori esercitazioni.