Circuito Serie RLC Risonante

Indice

Circuiti Risonanti serie RLC e formule della frequenza risonante , le frequenze di taglio sono sviluppate, la larghezza di banda e il fattore di qualità sono definiti e tutti sono utilizzati negli esempi con soluzioni dettagliate. \( \) \( \) \( \) \( \)
Di seguito, la lettera maiuscola \( I \) è la forma complessa (polare) della corrente reale \( i \) e la lettera maiuscola \( V_i \) è la forma complessa (polare) della tensione reale \( v_i \).
Un calcolatore di circuiti serie RLC risonanti può essere utilizzato per verificare i calcoli degli esempi seguenti e anche per ulteriori esercitazioni e indagini su questi circuiti.

A - Circuito serie RLC risonante

Considera il circuito serie RLC mostrato di seguito.

Per un circuito alimentato da una sorgente di tensione di frequenza \( f \), l'impedenza totale \( Z \) del circuito serie RLC è data da:
\[ Z = R + j \left(\omega L - \dfrac{1}{\omega C} \right) \]
La relazione tra la corrente \( I \) e la tensione \( V_i \) è data da
\[ I = \dfrac{V_i}{Z} \]
dove \( V_i \) e \( I \) sono la forma complessa della tensione \( v_i \) e la corrente \( i \) rispettivamente.
Utilizzando la definizione del modulo di un numero complesso, il modulo \( |Z| \) è dato da
\( |Z| = \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} \)
Se \( V_0 \) è il valore di picco della sorgente di tensione \( v_i = V_0 \cos (\omega t) \), allora il valore di picco \( I_0 \) di \( I \) è dato da
\( I_0 = \dfrac{V_0}{ |Z| } = \dfrac{V_0}{ \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} } \)
La frequenza di risonanza è definita come la frequenza per cui \( I_0 \) è massimo o quando il modulo di \( Z \) è minimo.
Poiché la resistenza \( R \) è indipendente dalla frequenza, il valore minimo di \( |Z| \) si verifica a \( \omega = \omega_r \) tale che
\( \left(\omega_r L - \dfrac{1}{\omega_r C} \right) = 0 \)
Risolvendo quanto sopra per \( \omega_r \) si ottiene la frequenza risonante
\[ \omega_r = \dfrac{1}{\sqrt {L C}} \quad \quad (I) \]
Alla frequenza risonante \( \omega = \omega_r \), abbiamo:
1) \( Z = R \)
Per \( V_0 \), il valore di picco della sorgente di tensione \( v_i \), il valore di picco \( I_0 \) di \( I \) è dato da
2) \( I_0 = \dfrac{V_0}{R} \)
Sia \( X_L = \omega L \) e \( X_C = \dfrac{1}{\omega C} \)
3) \( X_L = X_C \)

Esempio 1
Sia \( R=300 \; \Omega \), \( L = 100 \; mH \) e \( C = 100 \mu F \) nel circuito serie RLC sopra.
a) Trovare la frequenza risonante \( \omega_r \)
b) Graficare \( |Z| \), \( X_L = \omega L \), \( X_C = \dfrac{1}{\omega C} \) e \( I_0 \) come funzione della frequenza \( \omega \) e discutere i grafici ottenuti.

Soluzione all'Esempio 1
a)
La frequenza risonante \( \omega_r \) è data da
\( \omega_r = \dfrac{1}{\sqrt {L C}} = \dfrac{1}{\sqrt{100\times10^{-3} \times 100 \times 10^{-6}}} \approx 316.23\)
b)
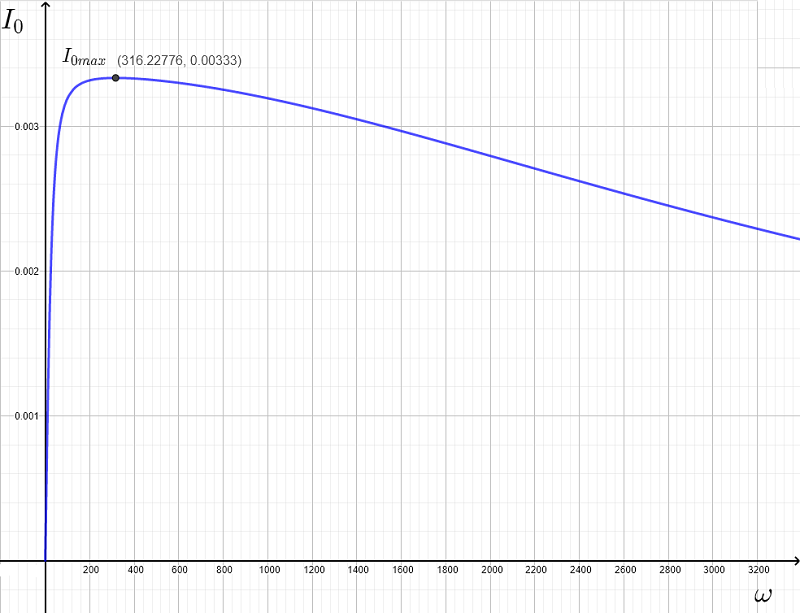
Di seguito sono mostrati i grafici di \( |Z| \), \( X_L \) e \( X_C \).
Dai grafici, \( |Z| \) ha un valore minimo pari a \( R = 300 \; \Omega \) (punto A)
I grafici di \( X_L \) e \( X_C \) si intersecano (punto B) e quindi \( X_L = X_C \) o \( \left(\omega_r L - \dfrac{1}{\omega_r C} \right) = 0 \) .



Nel grafico seguente è mostrata la corrente \( I_0 \) e è massima alla frequenza risonante \( \omega_r \approx 316.23\) (dopo l'arrotondamento a 2 cifre decimali)

B - Potenza Media in un Circuito Risonante

La potenza media \( P_a \) consegnata al circuito serie RLC è data da: \[ \displaystyle \quad \quad P_a = \dfrac{V_0^2}{2 |Z|} \cos \theta \quad \quad (II) \] dove \( \theta \) è l'argomento dell'impedenza \( Z = R + j \left(\omega L - \dfrac{1}{\omega C} \right) \) e è dato da
\( \theta = \arctan \left( \dfrac{ \omega L - \dfrac{1}{\omega C} }{R} \right) \)
Utilizzando le proprietà delle funzioni trigonometriche inverse, abbiamo
\( \tan \theta = \left( \dfrac{ \omega L - \dfrac{1}{\omega C} }{R} \right) \)
\( \theta \) può essere considerato come un angolo acuto di un triangolo rettangolo come mostrato di seguito. (Usa la definizione della tangente di un angolo in un triangolo rettangolo e osserva che puoi ottenere \( \tan \theta \) come definito sopra.)



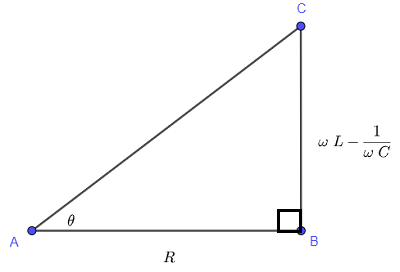
Usiamo ora lo stesso triangolo e calcoliamo il fattore di potenza \( \cos \theta \)
L'ipotenusa del triangolo è calcolata come segue
\( AC = \sqrt {R^2 + \left( \omega L - \dfrac{1}{\omega C} \right)^2} \)
\( \cos \theta = \dfrac{AB}{AC} = \dfrac{R}{\sqrt {R^2 + \left( \omega L - \dfrac{1}{\omega C} \right)^2}} \)
Sostituisci \( \cos \theta \) e \( |Z| \) nella formula (II) data sopra ed esprimi la potenza \( P_a \) come
\( \displaystyle \quad \quad P_a = \dfrac{V_0^2}{2 \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} }\dfrac{R}{\sqrt {R^2 + \left( \omega L - \dfrac{1}{\omega C} \right)^2}} \)
Semplifica
\[ \displaystyle \quad \quad P_a = \dfrac{V_0^2 R}{2 \left({R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} \right) } \quad \quad (III) \]
Alla frequenza risonante \( \omega_r = \dfrac{1}{\sqrt {LC}} \), abbiamo \( \left(\omega_r L - \dfrac{1}{\omega_r C} \right) = 0 \) e quindi la potenza è massima e uguale a \[ P_{a max} = \dfrac{V_0^2}{2 \; R} \quad \quad (IV) \]

C - Frequenze di Taglio di un Circuito Risonante e Fattore di Qualità

Definiamo ora le frequenze di taglio come le frequenze \( \omega_c \) a cui la potenza \( P_a(\omega) \) in (III) è la metà della potenza massima \( P_{a max} \) in (IV).
Dobbiamo quindi risolvere l'equazione
\( P_a (\omega_c ) = \dfrac{1}{2} \left(\dfrac{V_0^2}{2 \; R} \right) \)

\( \dfrac{V_0^2 R}{2 \left({R^2 + \left(\omega_c L - \dfrac{1}{\omega_c C} \right)^2} \right) } = \dfrac{1}{2} \dfrac{V_0^2}{2 \; R} \)
Semplifica a
\( \dfrac{ R}{2 \left({R^2 + \left(\omega_c L - \dfrac{1}{\omega_c C} \right)^2} \right) } = \dfrac{1}{4 R} \)
Moltiplica incrociato, semplifica e riscrivi l'equazione sopra come
\( (\omega_c L - \dfrac {1}{\omega_c C } ) = R^2 \)
Risolviamo estraendo la radice quadrata per ottenere due equazioni
\( \omega_c L - \dfrac {1}{\omega_c C} = \pm R \)
Moltiplica tutti i termini per \( \omega_c C \) e semplifica
\( \omega_c^2 L C \pm \omega_c R C - 1 = \pm \omega_c R C \)
Riscrivi come equazioni quadratiche in forma standard
\( \omega_c^2 L C \pm \omega_c R C - 1 = 0\)
Risolviamo la prima equazione quadratica \( \quad \omega_c^2 L C + \omega_c R C - 1 = 0\)
per ottenere due soluzioni
\( \omega_{c1} = \dfrac {- R C \pm \sqrt{ (R C)^2 + 4 L C }}{ 2 L C } \)

Risolviamo la seconda equazione quadratica \( \quad \omega_c^2 L C - \omega_c R C - 1=0\)
per ottenere due soluzioni
\( \omega_{c2} = \dfrac {R C \pm \sqrt{ (R C)^2 + 4 L C}}{ 2 L C } \)
Abbiamo un totale di 4 soluzioni. Nota che la quantità \( \sqrt{ (R C)^2 + 4 L C } \) è maggiore di \( RC \) e quindi solo due soluzioni sono valide poiché la frequenza di taglio è una quantità positiva.
Le frequenze di taglio \( \omega_{c1} \) e \( \omega_{c2} \) sono le due soluzioni date
\( \omega_{c1} = \dfrac {- R C + \sqrt{ (R C)^2 + 4 L C }}{ 2 L C } \)

\( \omega_{c2} = \dfrac {R C + \sqrt{ (R C)^2 + 4 L C}}{ 2 L C } \)
Abbiamo già trovato la frequenza risonante \( \omega_r = \dfrac{1}{\sqrt{LC}} \) Usa semplice algebra per riscrivere \( \omega_{c1} \) e \( \omega_{c1} \) in termini di \( \omega_r \)
\[ \omega_{c1} = - \dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} \quad \quad (V) \]
\[ \omega_{c2} = \dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} \quad \quad (VI) \]

Nota che
\[ \omega_{c1} \times \omega_{c2} = \omega_r^2 \quad \quad (VII) \]

La larghezza di banda del circuito risonante è definita da: \( \Delta \omega = \omega_{c2} - \omega_{c1} \)

Il fattore di qualità \( Q \) è definito da
\( Q = \dfrac{\omega_r}{\Delta \omega} \)
Sostituisci
\( Q = \dfrac {\omega_r} { \left(\dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} - \left(-\dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} \right) \right)} \)
Semplifica
\[ Q = \omega_r \dfrac{L}{R} \quad \quad (VIII) \]

D - Altri Esempi con Soluzioni Dettagliate

Esempio 3
Un circuito risonante serie RLC deve essere progettato in modo che abbia le frequenze \( f_{c_1} = 650 \) Hertz e \( f_{c_2} = 950 \) Hertz come frequenze di taglio inferiore e superiore.
a) Calcola la capacità del condensatore \( C \) e l'induttanza dell'induttore \( L \) se la resistenza della resistenza \( R \) è uguale a \( 30 \Omega \).
b) Qual è il fattore di qualità del circuito?

Soluzione all'Esempio 3
a)
Calcola le frequenze angolari.
\( \omega_{c_1} = 2 \pi f_{c_1} = 1300 \pi \) rad/s
\( \omega_{c_2} = 2 \pi f_{c_1} = 1900 \pi \) rad/s
Usa la formula (VII) sviluppata sopra
\( \omega_{c_1} \times \omega_{c_2} = \omega_{r}^2 \) per calcolare la frequenza risonante \( \omega_{r} \) del circuito.
\( \omega_{r} = \sqrt {\omega_{c_1} \times \omega_{c_2}} = \sqrt {1300 \pi \times 1900 \pi } = 100 \sqrt{247} \pi = 4937.400 \) rad/s
\( \omega_{c_2} - \omega_{c_1} = \dfrac{R}{L} \)
Quindi
\( L = \dfrac{R } {\omega_{c_2} - \omega_{c_1}} = \dfrac{30} {1900 \pi - 1300 \pi } = 0.01591 \) H
\( \omega_{r} = \dfrac{1}{\sqrt {L C} } \)
Quindi
\( C = \dfrac{1}{\omega_{r}^2 L} = \dfrac{1}{(100 \sqrt{247} \pi)^2 \times 0.01591} = 2.5783 \times 10^{-6} \) F

b)
Il fattore di qualità è dato da
\( Q = \dfrac{\omega_{r}}{\omega_{c_2} - \omega_{c_1}} = \dfrac{100 \sqrt{247} \pi}{1900 \pi - 1300 \pi } = 2.62\)

Altri Riferimenti e Link

• Calcolatore di Circuito Risonante Serie RLC
• Circuiti RLC in serie
• Calcolatore di Impedenza del Circuito Serie RLC
• Calcolatore di Impedenza del Circuito Parallelo RLC
• Calcolatore Grafico di Corrente Serie RLC