Calcoli di Corrente e Tensioni in un Circuito RLC in Serie

Indice

Si discute qui come impedenze complesse sono utilizzate per analizzare correnti e tensioni nei circuiti RLC in serie. I numeri complessi semplificano notevolmente i calcoli delle impedenze, delle correnti e delle tensioni nei circuiti CA.
Poiché il simbolo \( i \) è usato per le correnti nei circuiti CA, qui usiamo \( j \) come unità immaginaria definita da \( j^2 = -1 \) o \( j = \sqrt{-1} \)
Le lettere minuscole per corrente e tensioni vengono utilizzate per quantità reali. Le lettere maiuscole per corrente e tensioni vengono utilizzate per quantità complesse in forma polare.

A - Impedenze come Numeri Complessi e Fasori di un circuito RLC in serie

Per un circuito alimentato da una sorgente di tensione di frequenza \( f \), le impedenze dei diversi componenti RLC sono date da:
Le impedenze in forma complessa \( Z_R \) di una resistenza di resistenza \( R \) è data da \[ Z_R = R \] Le impedenze in forma complessa \( Z_L \) di un induttore di induttanza \( L \), anche chiamata reattanza induttiva, è data da \[ Z_L = j \omega L \] Le impedenze in forma complessa \( Z_C \) di un condensatore di capacità \( C \) , anche chiamata reattanza capacitiva, è data da \[ Z_C = - \dfrac{1}{\omega C} j \] dove \( \omega = 2 \pi f \)
La cosa più importante da notare è che le reattanze induttive e capacitive dipendono dalla frequenza della sorgente di tensione.

Sia \( V_i \), \( I \), \( V_R \), \( V_L \) e \( V_C \) la forma complessa di \( v_i \), \( i \), \( v_R \), \( v_L \) e \( v_C \) rispettivamente.
Applica la legge di Kirchhoff della tensione estesa alle impedenze complesse per scrivere
\( V_i - V_R - V_L - V_C = 0\)     (1)
Applica la legge di Ohm estesa alle impedenze complesse per scrivere
\( V_R = Z_R I \)
\( V_L = Z_L I \)
\( V_C = Z_C I \)
Sostituisci quanto sopra nell'equazione (1) per ottenere
\( V_i = Z_R I + Z_L I + Z_C I = 0\)
Risolvi quanto sopra per \( I \)
\( I = \dfrac{V_i}{Z_R + Z_L + Z_C } \)
Sia \( Z \) l'impedenza complessa equivalente del circuito RLC in serie definita come
\[ Z = Z_R + Z_L + Z_C = R + j \left(\omega L - \dfrac{1}{\omega C} \right) \]
Il modulo di \( Z \): \[ |Z| = \sqrt{R^2 + \left(\omega L - \dfrac{1}{\omega C}\right)^2} \]
L' argomento di \( Z \): \[ \theta = arctan \left( \dfrac {\omega L - \dfrac{1}{\omega C}}{R} \right) \]
Nota che sia il modulo che l'argomento dell'impedenza \( Z \) dipendono dalla frequenza (\( \omega = 2 \pi f \)) della sorgente di tensione. Questa proprietà è utile nella progettazione di filtri e ha molte altre applicazioni nei circuiti elettronici.
Scrivi \( Z \) in forma polare
\[ Z = |Z| \; \angle \; \theta \]
Le espressioni per \( Z_R, Z_L, Z_C \) e \( Z \), fatte sopra, potrebbero essere interpretate geometricamente usando fasori come mostrato di seguito.


Nella parte (a), \( Z_R, Z_L\) e \( Z_C \) sono rappresentati in un sistema di assi con la parte reale lungo l'asse orizzontale e la parte immaginaria lungo l'asse verticale.
Nella parte (b), \( Z = Z_R + Z_L + Z_C \) è tracciato geometricamente utilizzando l'addizione vettoriale (o numeri complessi)
Nella parte (c), un triangolo rettangolo con l'ipotenusa che rappresenta il modulo di \( Z \): utilizzando il teorema di Pitagora: \( |Z| = \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C}\right)^2} \) esattamente come ottenuto sopra utilizzando i numeri complessi.
Ancora utilizzando il triangolo rettangolo, l'angolo: \( \theta = \arctan \left (\dfrac{\omega L - \dfrac{1}{\omega C}}{R} \right) \)

B - Corrente e Tensioni di un circuito RLC in serie

Sia \( v_i = V_0 \cos ( \omega t) \) , \( V_0 \) il picco della tensione di ingresso
Formula di Euler dei numeri complessi
\( e^{j \omega t} = \cos (\omega t) + j \sin (\omega t )\)
Quindi \( v_i \) può essere scritto anche come
\( v_i \) è uguale alla parte reale di \( e^{j \omega t} \)
Ora tralasciamo la "Parte reale di" e facciamo tutti i calcoli in numeri complessi e definiamo \( V_i \) in forma complessa come
\( V_i = V_0 e^{j \omega t} \)
e deduciamo \( I \) in forma complessa
\( I = \frac{V_0 e^{j\omega t}}{|Z| \; \angle \; \theta} \)
e \( I \) in forma polare è dato da
\( I = \dfrac{V_0}{|Z|} \; \angle \; \omega t - \theta \)
\( I = I_0 \; \angle \; \omega t - \theta \) , dove \( I_0 = \dfrac{V_0}{|Z|} \)
Riscrivi le impedenze \( Z_R, Z_L\) e \( Z_C \) in forma polare
\( Z_R = R = R \; \angle \; 0 \)
\( Z_L = j \omega L = \omega L \; \angle \; \pi/2\)
\( Z_C = - \dfrac{1}{\omega C} j = \dfrac{1}{\omega C} \; \angle \; - \pi/2\ \)
Le tensioni sono date da
\( V_R = Z_R I = (R \; \angle \; 0) (I_0 \; \angle \; {\omega t - \theta}) = R I_0 \angle \; \omega t - \theta \)
\( V_L = Z_L I = (\omega L \; \angle \; \pi/2) (I_0 \; \angle \; {j\omega t - \theta}) = \omega L I_0 \; \angle \; {\omega t - \theta + \pi/2} \)
\( V_C = Z_C I = (\dfrac{1}{\omega C} \; \angle \; - \pi/2) (I_0 \; \angle \; {j\omega t - \theta}) = \dfrac{I_0}{\omega C} \; \angle \; {\omega t - \theta - \pi/2} \)
La corrente \( I \) e le tensioni \( V_R \) , \( V_C \) e \( V_C \) sono mostrate di seguito utilizzando fasori.

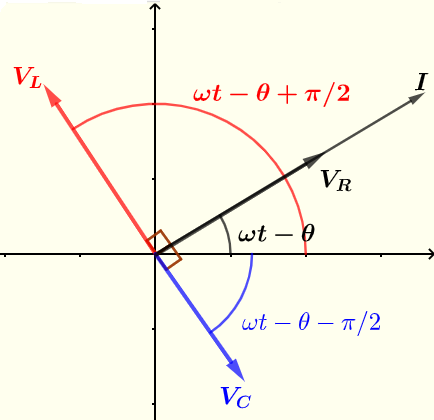
La corrente e le tensioni reali sono date dalla parte reale della forma complessa (o polare) della corrente e delle tensioni ottenute sopra.
\( i = \dfrac{V_0}{|Z|} \cos( \omega t - \theta) \)

\( v_R = R \dfrac{V_0}{|Z|} \cos(\omega t - \theta) \)

\( v_L = \omega L \dfrac{V_0}{|Z|} \cos(\omega t - \theta + \pi/2) \)

\( v_C = \dfrac{V_0}{\omega C|Z|} \cos(\omega t - \theta - \pi/2) \)

NOTA che la variazione nel tempo \( \omega t \) potrebbe essere omessa durante i calcoli e può essere aggiunta alla fine se necessario scrivere correnti e tensioni come funzione del tempo. Gli esempi di seguito mostrano come i circuiti RLC vengono analizzati ignorando la dipendenza dal tempo.

C - Esempi con Soluzioni Dettagliate

Esempio 1
In un circuito RLC in serie, la tensione di ingresso è data da \( v_i = 20 \cos (\omega t) \), dove \( \omega = 1000 \; rad/s \), la capacità del condensatore \( C = 200 \; \mu F \), l'induttanza dell'induttore \( L = 400 \; mH\) e la resistenza del resistore \( R = 400 \; \Omega \).
a) Trovare le impedenze del condensatore, dell'induttore e del resistore e l'impedenza \( Z \) equivalente al circuito RLC in forma complessa.
b) Trovare la corrente e tutte le tensioni in forma complessa.
c) Trovare la corrente e le tensioni reali.

Soluzione all'Esempio 1
a)
Le impedenze in forma complessa \( Z_R \) di una resistenza di resistenza \( R \) è data da
\( Z_R = R = 400 \; \Omega \)
Le impedenze in forma complessa \( Z_L \) di un induttore di induttanza \( L \), anche chiamata reattanza induttiva, è data da
\( Z_L = j \omega L = j \cdot 1000 \cdot 400 \cdot 10^{-3} = 400 j \; \Omega \)
Le impedenze in forma complessa \( Z_C \) di un condensatore di capacità \( C \) , anche chiamata reattanza capacitiva, è data da
\( Z_C = - \dfrac{1}{\omega C} j = - \dfrac{1}{1000 \cdot 200 \cdot 10^-6} j = - 5 j \; \Omega \)
\( Z = Z_R + Z_L + Z_C = 400 + 400 j - 5 j = 400 + 395 j \)
b)
\( v_i = 20 cos ( \omega t) \), quindi la forma polare della tensione di ingresso \( V_i = 20 \; \angle \; 0\)
Abbiamo visto sopra che la corrente in forma polare è data da
\( I = \dfrac{V_i}{Z_R + Z_L + Z_C } \)
Sostituisci le quantità note
\( I = \dfrac{20 \; \angle \; 0}{400 + 395 j}\)
Riscrivi il denominatore in forma polare
\( 400 + 395 j = \sqrt {400^2+395^2} \; \angle \; \arctan\left(\dfrac{395}{400}\right) = 562.16 \; \angle \; 44.64^{\circ} \)
Valuta \( I \)
\( I = \dfrac{20 \; \angle \; 0}{562.16 \; \angle \; 44.64^{\circ}} = \dfrac{20}{562.16} \; \angle \; 0 - 44.64^{\circ} \)
Semplifica
\( I = 0.0356 \; \; \angle \; - 44.64^{\circ} \) A
\( V_R = R I = 400 (0.0356 \; \; \angle \; - 44.64^{\circ}) = 14.24 \; V \; \angle \; - 44.64^{\circ}\) V
\( V_L = Z_L I = 400 j (0.0356 \; \; \angle \; - 44.64^{\circ}) = 14.24 \; V \; \angle \; 45.36^{\circ}\) V
\( V_C = Z_C I = - 5 j (0.0356 \; \; \angle \; - 44.64^{\circ}) = 0.18 \; V \; \angle \; -134.6^{\circ}\) V

Ulteriori Riferimenti e Link