Utilizzare i Numeri Complessi nei Circuiti CA

Tabella dei Contenuti

Viene qui discusso come i numeri complessi possono essere utilizzati per analizzare e calcolare correnti e tensioni nei circuiti CA (corrente alternata) e anche come la resistenza, l'impedenza di un condensatore e l'impedenza di un'induttanza sono rappresentate da numeri complessi. Viene inoltre mostrato come l'uso di impedenze complesse consenta l'uso di una legge simile alla legge di Ohm per modellare matematicamente i circuiti CA. Due motivi principali che rendono l'uso dei numeri complessi adatto per modellare i circuiti CA, e molti altri fenomeni a onde sinusoidali in diversi settori dell'ingegneria, sono:
1) i segnali CA (e molti altri fenomeni a onde sinusoidali) sono caratterizzati da una ampiezza e una fase che sono, rispettivamente, molto simili al modulo e all'argomento dei numeri complessi.
2) le operazioni di base come l'addizione, la sottrazione, la moltiplicazione e la divisione dei numeri complessi sono più facili da eseguire e da programmare su un computer.
Nota
1) Poiché il simbolo \( i \) è usato per le correnti nei circuiti CA, qui usiamo \( j \) come unità immaginaria definita da \( j^2 = -1 \) o \( j = \sqrt{-1} \)
2) Il simbolo \( \Re e\) rappresenta la parte reale di un numero complesso.

A - Parte Reale dei Numeri Complessi

Un numero complesso in forma standard \( Z = a + j b \) può essere scritto in forma esponenziale come segue
\( \displaystyle Z = r e^{j \theta} \)      con \( j^2 = -1 \)
e in forma polare come segue
\( Z = r \angle \theta \)
dove \( r = \sqrt{a^2 +b^2} \) è il modulo di \( Z \) e \( \tan \theta = \dfrac{b}{a} \) il suo argomento.
Prendi la parte reale, scritta come \( \Re e \) , di ciascun lato di un numero complesso in forma esponenziale
\( \Re e (r e^{j \theta}) = \Re e (r ( \cos \theta + j \sin \theta )) = \Re e (r \cos \theta + j r \sin \theta ) = r \cos \theta \)
In quello che segue, \( \Re e \) significa la parte reale di un dato numero complesso.

B - Derivata delle Funzioni Complesse con una Variabile

Sia \( f(t) \) una funzione complessa con una variabile \( t \) scritta nella forma
\( f(t) = a(t) + j b(t) \)
dove \( a(t) \) è la parte reale di \( f(t) \), \( b(t) \) è la parte immaginaria di \( f(t) \) e \( j = \sqrt {-1}\) è l'unità immaginaria.
Sia \( f'(t) \) la prima derivata di \( f(t) \) rispetto a \( t \) definita da
\( f'(t) = \lim_{h\to 0} \dfrac{f(t+h) - f(t) }{h} \)
Sostituisci \( f(t+h) \) con \( a(t+h) + j b(t+h) \) nella formula sopra.
\( f'(t) = \lim_{h\to 0} \dfrac{ a(t+h) + j b(t+h) - (a(t) + jb(t))}{h} \)
Separa i termini come segue
\( f'(t) = \lim_{h\to 0} \dfrac{ a(t+h) - a(t)}{h} + j \lim_{h\to 0} \dfrac{ j b(t+h) - jb(t)) }{h} \)
\( f'(t) = a'(t) + j b'(t) \)
È ora facile mostrare che la parte reale della derivata di \( f(t) \) è uguale a la derivata della parte reale di \( f(t) \) che può essere scritta come
\( \Re e(f'(t)) = a'(t) = (\Re e(f(t))' \)
o
\( \Re e \left ( \dfrac{df(t)}{dt} \right) = \dfrac {d a(t)}{dt} = \dfrac {d \left (\Re e(f(t)) \right)}{dt} \)

C - Integrale di Funzioni Complesse con una Variabile

Sia \( f(t) \) una funzione complessa con una variabile \( t \) scritta nella forma
\( f(t) = a(t) + j b(t) \)
dove \( a(t) \) è la parte reale di \( f(t) \), \( b(t) \) è la parte immaginaria di \( f(t) \) e \( j = \sqrt {-1}\) è l'unità immaginaria.
Sia \( F(t) \) definita dall'integrale indefinito
\( \displaystyle F(t) = \int f(t) dt = \int (a(t) + j b(t)) dt = \int a(t) dt + j \int b(t) dt \)
È ora facile mostrare che la parte reale dell'integrale di \( f(t) \) è uguale a l'integrale indefinito della parte reale di \( f(t) \) che può essere scritto come
\( \displaystyle \Re e \left( \int f(t) dt \right) = \int a(t) dt = \int \left( \Re e f(t) \right) dt \)

Utilizziamo ora i concetti sopra esposti per analizzare semplici circuiti CA utilizzando numeri complessi.

D - Sorgente di Tensione CA e Numeri Complessi

In quello che segue, \( v(t) \) è una sorgente di tensione CA, che varia nel tempo \( t \), data da
\( v(t) = V_0 \cos(\omega t) \)
dove \( V_0 \) è un numero reale uguale alla tensione di picco e \( \omega = 2 \pi f \) è anch'esso un numero reale con \( f \) la frequenza della sorgente di tensione.
Utilizzando numeri complessi, \( v(t) \) può essere scritto anche come
\( v(t) = V_0 \cos(\omega t) = \Re e ( V_0 \cos(\omega t) + j V_0 \sin(\omega t) ) = \Re e (V_0 e^{j\omega t} ) \)

E - Resistore in un circuito CA

Consideriamo un semplice circuito CA con un resistore come mostrato di seguito. Sia \( v(t) \) una sorgente di tensione CA data da
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
dove \( V_0 \) e \( \omega \) sono quantità reali.


La relazione tra la corrente \( i \) attraverso e la tensione \( v(t)_R \) attraverso il resistore \( R \) è data da
\( v(t)_R = R i \)
Utilizzando il singolo loop mostrato sopra, abbiamo
\( v(t) = v(t)_R \)
\( v(t) \) è data da \( v(t) = V_0 \cos(\omega t) \)
quindi
\( v(t)_R = V_0 cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
combinando quanto sopra, scriviamo
\( R i = \Re e (V_0 e^{j\omega t} ) \)       (I)
Sia \( V_R = V_0 e^{j\omega t} \) e riscriviamo (I) come
\( R i = \Re e V_R \)
poiché \( R \) è una quantità reale, quanto sopra può essere scritto come
\( i = \Re e \left( \dfrac{V_R }{R} \right) \)
Sia \( Z_R \) definito come l'impedenza di un resistore in modo che
\( Z_R = R \)
Poiché \( R \) è reale, l'impedenza \( Z_R \) di un resistore è un numero reale.
La corrente \( i \) può quindi essere scritta come
\( i = \Re e \left( \dfrac{ V_R } {Z_R} \right) \)
Sia
\( I = \dfrac{ V_R } {Z_R} \)
Quanto sopra fornisce una relazione simile alla legge di Ohm nei circuiti a corrente continua (CC). La relazione tra le grandezze complesse \( I \), \( V_R \) e \( R \) semplifica i calcoli.
Ciò semplifica i calcoli nel senso che eseguiamo i calcoli utilizzando impedenze complesse, tensione e corrente e poi prendiamo la parte reale come risposta finale.

F - Condensatore in un circuito CA

Consideriamo un semplice circuito CA con un condensatore come mostrato di seguito. Sia \( v(t) \) una sorgente di tensione CA data da
\( v(t) = V_0 cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)

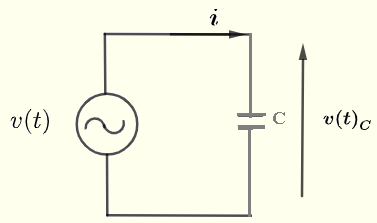
La relazione tra la corrente \( i \) attraverso e la tensione \( v(t)_C \) attraverso il condensatore \( C \) è data da
\( \displaystyle v(t)_C = \dfrac{1}{C } \ int i dt \)
Utilizzando il singolo loop mostrato sopra, abbiamo
\( v(t) = v(t)_C \)
Dato
\( v(t) = V_0 cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
combiamo tutto quanto sopra per scrivere
\( \displaystyle \Re e (V_0 e^{j\omega t} ) = \dfrac{1}{C} \int i dt \)
Prendiamo la derivata di entrambi i lati
\( \displaystyle \dfrac{d}{dt} (\Re e (V_0 e^{j\omega t}) ) = \dfrac{d}{dt} \left(\dfrac{1}{C} \int i dt \right) \)
Utilizziamo il risultato sopra discusso nella parte B sopra, riscriviamo quanto sopra come
\( \displaystyle \Re e \dfrac{d}{dt} \left( V_0 e^{j\omega t} \right) = \dfrac{d}{dt} \left(\dfrac{1}{C} \int i dt \right) \)
Semplifichiamo
\( \Re e \left( j \omega V_0 e^{j\omega t} \right) = \dfrac{1}{C} i \)
Poiché la capacità \( C \) è una quantità reale, possiamo scrivere
\( i = \Re e \left( j \omega C \; V_0 e^{j\omega t} \right) \)
Sia \( V_C = V_0 e^{j\omega t} \) e definiamo \( Z_C \) come l'impedenza complessa di un condensatore in modo che
\( Z_C = \dfrac{1}{j \omega C} = - \dfrac {j} { \omega C} \)
Poiché \( C \) è reale, l'impedenza \( Z_C \) di un condensatore è un numero puramente immaginario.
La corrente \( i \) può quindi essere scritta come
\( i = \Re e \left( \dfrac{ V_C } {Z_C} \right) \)
Sia
\( I = \dfrac{ V_C } {Z_C} \)
Quanto sopra è simile alla legge di Ohm nei circuiti a corrente continua (CC). La relazione tra le grandezze complesse \( I \), \( V_C \) e \( Z_C \) semplifica i calcoli.
Ciò semplifica i calcoli nel senso che eseguiamo i calcoli utilizzando impedenze complesse, tensione e corrente e poi prendiamo la parte reale come risposta finale.

G - Induttore in un circuito CA

Consideriamo un semplice circuito CA con un condensatore come mostrato di seguito. Sia \( v(t) \) una sorgente di tensione CA data da
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)

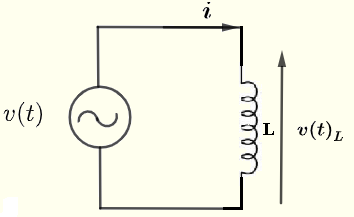
La relazione tra la corrente \( i \) attraverso e la tensione \( v(t)_L \) attraverso l'induttore con induttanza \( L \) è data da
\( v(t)_L = L \dfrac {d i}{ dt} \)
Utilizzando il singolo loop mostrato sopra, abbiamo
\( v(t) = v(t)_L \)
Dato
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
combiamo tutto quanto sopra per scrivere
\( \Re e (V_0 e^{j\omega t} ) = L \dfrac {d i}{ dt} \)
Prendiamo l'integrale indefinito di entrambi i lati
\( \displaystyle \int \Re e (V_0 e^{j\omega t}) dt = \int L \dfrac {d i}{ dt} dt \)
Usiamo il risultato già discusso nella parte C sopra, riscriviamo quanto sopra come
\( \displaystyle \Re e \int V_0 e^{j\omega t} dt = \int L \dfrac {d i}{ dt} dt \)
Calcoliamo gli integrali su entrambi i lati
\( \Re e \left( \dfrac{1}{j\omega} V_0 e^{j\omega t} \right) = L i \)
Poiché l'induttanza \( L \) è una quantità reale, possiamo scrivere
\( i = \Re e \left( \dfrac{1}{j \omega L} \; V_0 e^{j\omega t} \right) \)
Sia \( V_L = V_0 e^{j\omega t} \) e \( Z_L \) sia definito come l'impedenza di un induttore in modo che
\( Z_L = j \omega L \)
Poiché \( L \) è reale, l'impedenza \( Z_L \) di un condensatore è un numero puramente immaginario.
La corrente \( i \) può quindi essere scritta come
\( i = \Re e \left( \dfrac{ V_L } {Z_L} \right) \)
Sia
\( I = \dfrac{ V_L } {Z_L} \)
Quanto sopra fornisce una relazione simile alla legge di Ohm tra le grandezze complesse \( I \), \( V_L \) e \( Z_L \).
Ciò semplifica i calcoli nel senso che eseguiamo i calcoli utilizzando l'impedenza complessa, tensione e corrente e poi prendiamo la parte reale come risposta finale.

H - Conclusion: Legge di Ohm con Impedenze Complesse

Abbiamo visto sopra che le impedenze di resistori, condensatori e induttori possono essere definite come quantità complesse che possono essere puramente reali o puramente immaginarie, date da
1) Per un resistore \( R\) ; l'impedenza è data da \[ Z_R = R \] e la relazione tra la corrente \( I \) (in forma complessa) attraverso e la tensione \( V_R \) (in forma complessa) attraverso il resistore \( R \) è la legge di Ohm in CA e è data da: \[ I = \dfrac{V_R}{Z_R} \] 2) Per un condensatore \( C \) ; l'impedenza è data da \[ Z_C = -\dfrac{j}{\omega C} \] e la relazione tra la corrente \( I \) (in forma complessa) attraverso e la tensione \( V_C \) (in forma complessa) attraverso il condensatore \( C \) è la legge di Ohm in CA e è data da: \[ I = \dfrac{V_C}{Z_C} \] 3) Per un induttore \( L \) ; l'impedenza è data da \[ Z_L = j \omega L \] e la relazione tra la corrente \( I \) (in forma complessa) attraverso e la tensione \( V_L \) (in forma complessa) attraverso l'induttore \( L \) è la legge di Ohm in AC e è data da: \[ I = \dfrac{V_C}{Z_L} \] Concludiamo che la legge di Ohm è valida nei circuiti CA quando si usano numeri complessi per modellare le impedenze di resistori, condensatori e induttori.
Si può anche dimostrare che le leggi di Kirchhoff sono valide nei circuiti CA quando si usano numeri complessi per modellare le impedenze di resistori, condensatori e induttori.
Le impedenze equivalenti a impedenze in serie e in parallelo possono essere calcolate utilizzando regole simili per resistori in serie e in parallelo.

E - Esempi con Soluzioni

Esempio 1
Trova la corrente \( i \), la tensione \( v(t)_R \) attraverso il resistore \( R \) e la tensione \( v(t)_L \) attraverso l'induttore \( L \) in termini di \( V_0 \), \( R \), \( L \) e \( \omega \) dato
sorgente di tensione: \( v(t) = V_0 \cos(\omega t) \) , \( \omega = 2 \pi f \) e \( f \) è la frequenza.

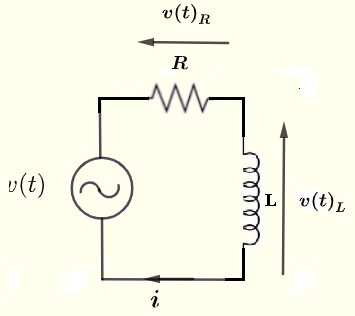
Soluzione per Esempio 1
Sia \( V \) la forma complessa della sorgente di tensione \( v(t) \).
Sia \( V_R \) la forma complessa della tensione \( v(t)_R\) attraverso il resistore R.
Sia \( V_L \) la forma complessa della tensione \( v(t)_L\) attraverso l'induttore L
Sia \( I \) la forma complessa della corrente \( i \) attraverso il resistore e il condensatore nel circuito dato.
Sia l'impedenza complessa di un resistore \( Z_R = R \) e quella dell'induttore \( Z_L = j \omega L \) (vedi parte H sopra).
Ridisegna il circuito con le quantità complesse definite sopra e puoi applicare le leggi di Ohm e Kirchhoff.

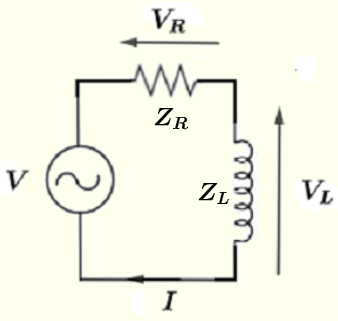
Utilizzando la legge di Kirchhoff sul loop che compone il circuito, abbiamo
\( V = V_R + V_L \)         (I)
Utilizzando la legge di Ohm per riscrivere \( V_R \) e \( V_L \) come
\( V_R = Z_R I \)
\( V_L = Z_L I \)
Sostituisci nell'equazione (I)
\( V = Z_R I + Z_L I = R I + j \omega L I = I(R + j \omega L ) \)
Risolvere quanto sopra per \( I \)
\( I = \dfrac{V}{R+j \omega L} \)         (II)
Il denominatore \( R+j \omega L \) è un numero complesso che può essere scritto in forma complessa come
\( R+j \omega L = r e^{j\theta} \)
dove
\( r = |Z| = \sqrt {R^2 + (L\omega)^2} \) è il modulo
\( \theta = \arctan \left(\dfrac{\omega L}{R} \right) \) è l'argomento come mostrato nel piano complesso sotto.

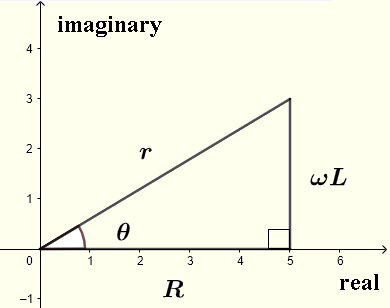
Sia \( V = V_0 e^{j\omega t} \)
Sostituisci \( V \) e \( R+j \omega L \) con le loro forme complesse in (II) e scrivi
\( I = \dfrac{V_0 e^{j\omega t}}{r e^{j\theta}} \)
Usa le regole esponenziali per semplificare quanto sopra
\( I = \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
Usa la legge di Ohm per scrivere
\( V_R = R I = \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)

\( V_L = Z_L I = \dfrac{j V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
Scrivi \( j \) in forma esponenziale \( j = e^{j \pi/2} \)in \( V_L \)
\( V_L = \dfrac{ e^{j \pi/2} V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
Usa la regola esponenziale per riscrivere quanto sopra come
\( V_L = \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t + \pi/2 -\theta)} \)
Ora usiamo le quantità complesse calcolate sopra per calcolare \( i \), \( v(t)_R \) e \( v(t)_L \) prendendo le parti reali come segue:
\( i = \Re e I = \Re e \left( \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \right) \)
che dà
\[ i = \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t-\theta) \] \( v(t)_R = \Re e V_R = \Re e \left( \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \right) \) \[ v(t)_R = \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t-\theta) \] \( v(t)_L = \Re e V_L = \Re e \left( \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t + \pi/2 -\theta)} \right) \) \[ v(t)_L = \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t + \pi/2 -\theta) \]

Altre Referenze e Link