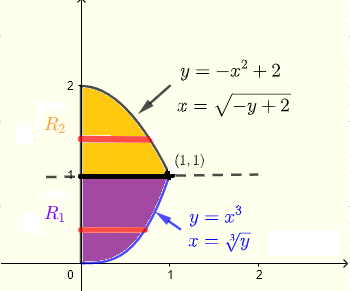Inhaltsverzeichnis
Doppelintegrale über allgemeine Bereiche
Beispiele zur Berechnung und Auswertung von Doppelintegralen über allgemeine Bereiche werden zusammen mit ihren detaillierten Lösungen präsentiert.
Wichtige Hinweise
1) Das Erstellen von Grafiken und Diagrammen für allgemeine nicht rechteckige Bereiche als erster Schritt erleichtert die Berechnung von Doppelintegralen mit allgemeinen Bereichen.
2) Im Allgemeinen sind vier Schritte erforderlich, um Doppelintegrale über allgemeine Integrationsbereiche zu berechnen:
SCHRITT 1: Erstellen Sie ein Diagramm und/oder eine Grafik des Integrationsbereichs.
SCHRITT 2: Entscheiden Sie, wie Sie den allgemeinen Bereich entweder mit vertikalen oder horizontalen Streifen beschreiben und somit die Reihenfolge der Integration festlegen.
SCHRITT 3: Beschreiben Sie den allgemeinen Integrationsbereich mit Ungleichungen.
SCHRITT 4: Berechnen Sie das Integral.
3) Im Folgenden beschreiben wir einen gegebenen Bereich \( R \) der Integration entweder als eine unendliche Menge von vertikalen Streifen, die es ermöglicht, das Integral als \( \displaystyle \iint_R f(x,y) \;dy \;dx \) auszudrücken, oder als horizontale Streifen, die es ermöglicht, das Integral als \( \displaystyle \iint_R f(x,y) \;dx \;dy \) auszudrücken.
Berechnungen von Doppelintegralen über allgemeine Bereiche
Das Ziel der Beispiele 1 und 2 ist es, anhand von Grafiken und Diagrammen die Integrationsgrenzen für allgemeine Bereiche zu bestimmen und das Doppelintegral zu berechnen.
Beispiel 1
Frage: Berechnen Sie das Doppelintegral \( \displaystyle V = \iint_R (x^2+y) \;dy \;dx \), wobei der Bereich \( R \) ein Dreieck in der \( xy\)-Ebene ist, das durch die \(x\)-Achse, die \(y\)-Achse und die Linie \( y = - x + 2 \) begrenzt wird.
Lösung zu Beispiel 1
Vier Hauptschritte zur Berechnung von Doppelintegralen mit allgemeinen Integrationsbereichen.
SCHRITT 1 Erstellen Sie ein Diagramm und/oder eine Grafik, die den allgemeinen Bereich darstellt.
Wir beginnen mit dem Zeichnen eines Diagramms oder einer Grafik des Integrationsbereichs \( R \). In diesem Beispiel ist es ein Dreieck mit Seiten auf den \(x\)- und \(y\)-Achsen, und die dritte Seite wird durch die Gleichung der Linie \( y = - x + 2 \) beschrieben.
Dieses Dreieck kann auch durch drei Eckpunkte definiert werden: den Ursprung und die Schnittpunkte der Linie \( y = - x + 2 \) mit den Achsen \( x \) und \( y \), die durch die Punkte \( (2,0) \) und \( (0,2) \) dargestellt werden, wie im untenstehenden Diagramm gezeigt.

Es gibt zwei Möglichkeiten, das gegebene Integral über den gegebenen Bereich zu berechnen.
SCHRITT 2 Entscheiden Sie, wie Sie den allgemeinen Bereich mithilfe von Streifen beschreiben.
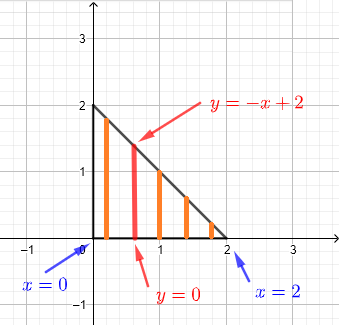
1) Wir verwenden vertikale Streifen, um den Bereich \( R \) zu beschreiben, wie im untenstehenden Diagramm gezeigt.
Wir gehen davon aus, dass der Bereich R als eine unendliche Menge vertikaler Streifen betrachtet werden kann, wie im untenstehenden Diagramm gezeigt.
Ein gegebener vertikaler Streifen beginnt bei \( y = 0 \) und endet bei \( y = - x + 2 \). Da alle Streifen, die den Bereich \( R \) beschreiben, enthalten sein müssen, muss \( x \) Werte von \( x = 0 \) bis \( x = 2 \) annehmen. Daher kann der Integrationsbereich \( R \) durch folgende Ungleichungen definiert werden:
SCHRITT 3 Beschreiben Sie den allgemeinen Integrationsbereich mit Ungleichungen.
\( R \) : \( 0 \le x \le 2 \) , \( 0 \le y \le - x + 2 \)
SCHRITT 4 Berechnen Sie das Integral.
Das Integral kann wie folgt geschrieben werden:
\( \displaystyle V = \int_0^2 \int_0^{-x+2} (x^2+y) \;dy \;dx \)
\( = \displaystyle \int_0^2 ( -x^3 +\dfrac{5}{2} x^2 - 2x + 2) \;dx = 8/3\)
Wir beantworten nun dieselbe Frage, aber unter Verwendung horizontaler Streifen.
SCHRITT 1 ist derselbe wie oben
SCHRITT 2 Entscheiden Sie, wie Sie den allgemeinen Bereich mithilfe von Streifen beschreiben.
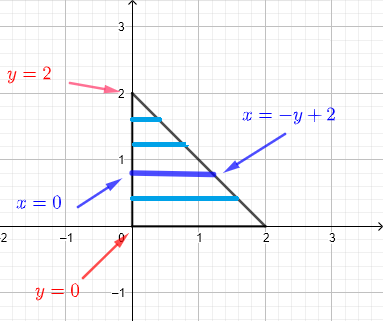
2) Wir verwenden horizontale Streifen, um den Bereich \( R \) zu beschreiben, wie im untenstehenden Diagramm gezeigt.
Wir gehen davon aus, dass der Bereich R als eine unendliche Menge horizontaler Streifen betrachtet werden kann, wie im untenstehenden Diagramm gezeigt.
Ein gegebener horizontaler Streifen beginnt bei \( x = 0 \) und endet bei \( x = - y + 2 \). Da alle Streifen enthalten sein müssen, um den Bereich \( R \) zu beschreiben, muss \( y \) Werte von \( y = 0 \) bis \( y = 2 \) annehmen. Daher kann der Integrationsbereich \( R \) durch folgende Ungleichungen definiert werden:
SCHRITT 3 Beschreiben Sie den allgemeinen Integrationsbereich mit Ungleichungen.
\( R \) : \( 0 \le x \le - y + 2 \) , \( 0 \le y \le 2 \)
SCHRITT 4 Berechnen Sie das Integral.
Das Integral kann wie folgt geschrieben werden:
\( \displaystyle V = \int_0^2 \int_0^{-y+2} (x^2+y) \;dx \;dy \)
\( = \displaystyle \int_0^2 (-\dfrac{1}{3} y^3 + y^2 - 2 y + \dfrac{8}{3} ) \;dy = 8/3 \)
Hinweise In beiden Fällen ist das Integral, dessen Grenzen Variablen enthalten, das innere Integral.
Beispiel 2
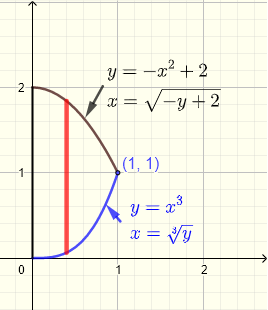
Frage: Berechnen Sie das Doppelintegral \( \displaystyle V = \iint_R (x+y) \;dy \;dx \), wobei der Bereich \( R \) auf der \( xy\)-Ebene durch die \(y\)-Achse und die Kurven der Gleichungen \( y = x^3 \) und \( y = - x^2 + 2 \) begrenzt wird.
Lösung zu Beispiel 2
Wir beginnen mit der Analyse des Bereichs \( R \), wie im untenstehenden Diagramm gezeigt. Die beiden Kurven schneiden sich an einem Punkt, dessen \( x \)-Koordinate durch die Lösung des Gleichungssystems gegeben ist:
\( y = x^3 \)
\(y = - x^2 + 2 \)
Eine Möglichkeit, das oben genannte System zu lösen, besteht darin, die beiden Gleichungen zu subtrahieren und zu vereinfachen, um \( y \) zu eliminieren und nur eine Gleichung in \(x \) zu erhalten, um die Gleichung zu erhalten:
\( 0 = x^3 + x^2 - 2 \)
Mit Hilfe des Diagramms ist es leicht zu erkennen, dass \( x = 1 \) eine Lösung des obigen Gleichungssystems ist, was Sie analytisch überprüfen können.
Die \(y\)-Koordinate des Schnittpunkts der beiden Kurven wird gefunden, indem \( x \) durch die bereits gefundene Lösung \( 1 \) in eine der Gleichungen der Kurven eingesetzt wird, um \( y = (1)^3 = 1 \) zu finden.
Daher ist der Schnittpunkt durch \( (1,1) \) gegeben.
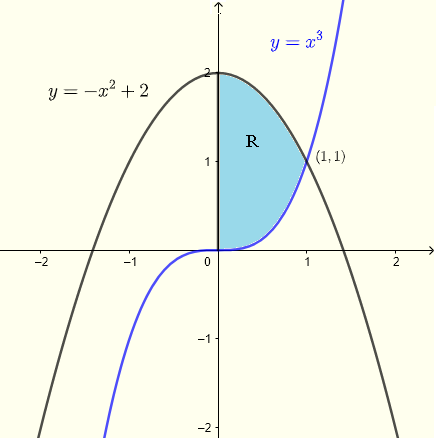
1) Unter Verwendung von vertikalen Streifen
Ein gegebener vertikaler Streifen beginnt auf der Kurve \( y = x^3 \) und endet auf der Kurve \( x = - x^2 + 2 \). Für den gesamten Bereich muss \( x \) alle Werte von \( x = 0 \) bis \( x = 1 \) annehmen. Daher ist der Integrationsbereich \( R \) gegeben durch:
\( R \) : \( 0 \le x \le 1 \) , \( x^3 \le y \le - x^2 + 2 \)
Daher kann das Integral wie folgt berechnet werden:
\( \displaystyle V = \int_0^1 \int_{x^3}^{-x^2+2} (x+y) \;dy \;dx = \dfrac{803}{420}\)
2) Unter Verwendung von horizontalen Streifen
Ein gegebener horizontaler Streifen beginnt an der \(y\)-Achse \( x = 0 \) und endet entweder auf der Kurve \( x = \sqrt[3]y \) oder auf der Kurve \( x = \sqrt{- y+ 2} \). Aufgrund der beiden verschiedenen Kurven kann der Bereich \( R \) in zwei Bereiche \( R_1 \) und \( R_2 \) unterteilt werden.
Für den Bereich \( R_1 \) muss \( y \) alle Werte von \( y = 0 \) bis \( y = 1 \) annehmen, und für den Bereich \( R_2 \) muss \( y \) alle Werte von \( y = 1 \) bis \( y = 2 \) annehmen.
Daher hat der Integrationsbereich \( R \) zwei Teile:
\( R_1 \) : \( 0 \le x \le \sqrt[3]y \) , \( 0 \le y \le 1 \)
und
\( R_2 \) : \( 0 \le x \le \sqrt{- y+ 2} \) , \( 1 \le y \le 2 \)
Daher kann das Integral wie folgt berechnet werden:
\( \displaystyle V = \iint_{R_1} (x+y) \;dx \;dy + \iint_{R_2} (x+y) \;dx \;dy \)
\( \displaystyle = \int_0^1 \int_{0}^{\sqrt[3]y} (x+y) \;dx \;dy + \int_1^2 \int_{0}^{\sqrt{-y+2}} (x+y) \;dx \;dy = \dfrac{803}{420}\)
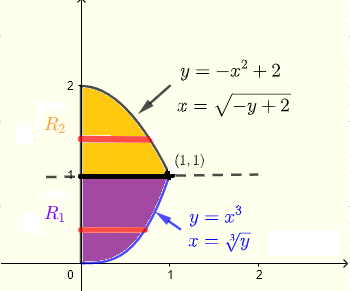
Beispiele, bei denen die Wahl der Integrationsreihenfolge von der gegebenen Aufgabe abhängt
In den Beispielen 3, 4 und 5 zeigen wir, dass es manchmal nicht möglich ist, die Reihenfolge der Integration wie gewöhnlich bei Doppelintegralen zu wählen.
Das Ziel der Beispiele 3, 4 und 5 ist es, anhand von Grafiken und Diagrammen die Integrationsreihenfolge zu bestimmen, die zur analytischen Berechnung des Doppelintegrals führt.
Beispiel 3
Frage: Bewerten Sie das Doppelintegral \( \displaystyle V = \int _0^1 \int _y^1 (y + e^{-x^2}) dx dy \), wenn möglich. Ändern Sie die Reihenfolge der Integration, wenn dies zur Auswertung des gegebenen Integrals erforderlich ist.
Lösung zu Beispiel 3
Beginnen wir mit dem inneren Integral.
Sei
\( \displaystyle I = \int _y^1 (y+e^{-x^2}) dx \)
Bei dem Versuch, \( I \) auszuwerten, kann das Integral \( \displaystyle I = \int _y^1 (e^{-x^2}) dx \) nicht analytisch gelöst werden.
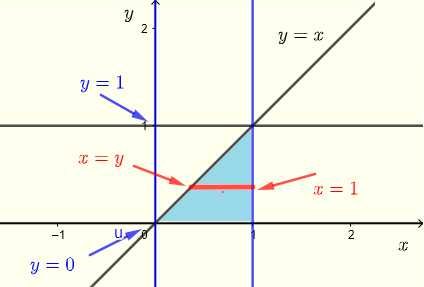
Gemäß den gegebenen Integrationsgrenzen kann der Integrationsbereich \( R \) des Integrals \( V \) wie folgt beschrieben werden:
\( R \) : \( y \le x \le 1 \) , \( 0 \le y \le 1 \)
mit dem unten gezeigten Diagramm als einer Reihe horizontaler Streifen.
Lassen Sie uns nun vertikale Streifen verwenden, um den Bereich \( R \) zu beschreiben, wie im untenstehenden Diagramm gezeigt.
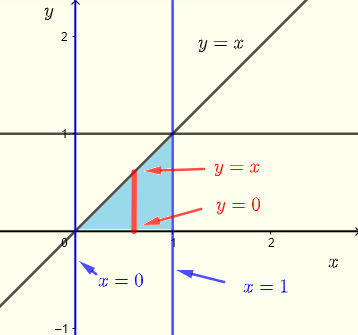
Graphieren Sie den Bereich \( R \) der Integration, um zu sehen, ob durch Ändern der Integrationsreihenfolge eine weitere Vorgehensweise möglich ist.
\( R \) : \( 0 \le x \le 1 \) , \( 0 \le y \le x \)
Das Integral \( V \) kann wie folgt geschrieben werden:
\( \displaystyle V
-------------------------------------------------------------------------------------
kann daher wie folgt geschrieben werden:
\( \displaystyle V = \int_0^2 \int_0^{-y+2} (x^2+y) \;dx \;dy \)
\( = \displaystyle \int_0^2 (-\dfrac{1}{3} y^3 + y^2 - 2 y + \dfrac{8}{3} ) \;dy = 8/3 \)
Hinweis: In beiden Fällen ist das Integral, dessen Grenzen Variablen enthalten, das innere Integral.
Beispiel 2
Frage: Berechnen Sie das Doppelintegral \( \displaystyle V = \iint_R (x+y) \;dy \;dx \), wobei der Bereich \( R \) in der \( xy\)-Ebene liegt und durch die \( y \)-Achse, die Kurven mit den Gleichungen \( y = x^3 \) und \( y = - x^2 + 2 \) begrenzt ist.
Lösung zu Beispiel 2
Wir beginnen mit der Analyse des Bereichs \( R \), wie im untenstehenden Diagramm gezeigt. Die beiden Kurven schneiden sich in einem Punkt, dessen \( x \)-Koordinate durch die Lösung des Gleichungssystems gegeben ist:
\( y = x^3 \)
\( y = - x^2 + 2 \)
Eine Möglichkeit, das obige System zu lösen, besteht darin, die beiden Gleichungen voneinander abzuziehen und zu vereinfachen, um \( y \) zu eliminieren und eine Gleichung in \( x \) zu erhalten:
\( 0 = x^3 + x^2 - 2 \)
Mit Hilfe des Diagramms ist leicht zu erkennen, dass \( x = 1 \) eine Lösung des obigen Gleichungssystems ist, was Sie analytisch überprüfen können.
Die \( y \)-Koordinate des Schnittpunkts der beiden Kurven wird gefunden, indem \( x \) durch die bereits gefundene Lösung \( 1 \) in eine der Gleichungen der Kurven eingesetzt wird, um \( y = (1)^3 = 1 \) zu erhalten.
Daher ist der Schnittpunkt gegeben durch \( (1,1) \).

1) Verwendung von vertikalen Streifen
Ein gegebener vertikaler Streifen beginnt auf der Kurve \( y = x^3 \) und endet auf der Kurve \( x = - x^2 + 2 \). Für den gesamten Bereich muss \( x \) alle Werte von \( x = 0 \) bis \( x = 1 \) annehmen. Daher ist der Bereich \( R \) der Integration durch folgende Ungleichungen gegeben:
\( R \) : \( 0 \le x \le 1 \) , \( x^3 \le y \le - x^2 + 2 \)
Das Integral kann daher wie folgt berechnet werden:
\( \displaystyle V = \int_0^1 \int_{x^3}^{-x^2+2} (x+y) \;dy \;dx = \dfrac{803}{420}\)

2) Verwendung von horizontalen Streifen
Ein gegebener horizontaler Streifen beginnt an der \( y \)-Achse \( x = 0 \) und endet entweder auf der Kurve \( x = \sqrt[3]{y} \) oder auf der Kurve \( x = \sqrt{- y + 2} \). Aufgrund der beiden verschiedenen Kurven kann der Bereich \( R \) in zwei Bereiche \( R_1 \) und \( R_2 \) aufgeteilt werden.
Für den Bereich \( R_1 \) muss \( y \) alle Werte von \( y = 0 \) bis \( y = 1 \) annehmen, und für den Bereich \( R_2 \) muss \( y \) alle Werte von \( y = 1 \) bis \( y = 2 \) annehmen.
Daher hat der Integrationsbereich \( R \) zwei Teile:
\( R_1 \) : \( 0 \le x \le \sqrt[3]{y} \) , \( 0 \le y \le 1 \)
und
\( R_2 \) : \( 0 \le x \le \sqrt{- y + 2} \) , \( 1 \le y \le 2 \)
Daher kann das Integral wie folgt berechnet werden:
\( \displaystyle V = \iint_{R_1} (x+y) \;dx \;dy + \iint_{R_2} (x+y) \;dx \;dy \)
\( \displaystyle = \int_0^1 \int_{0}^{\sqrt[3]{y}} (x+y) \;dx \;dy + \int_1^2 \int_{0}^{\sqrt{-y+2}} (x+y) \;dx \;dy = \dfrac{803}{420}\)
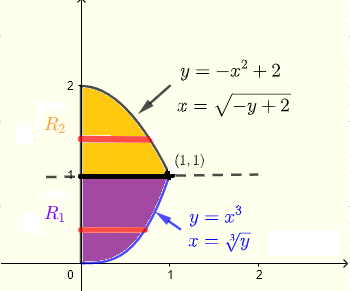
Beispiele, bei denen die Wahl der Integrationsreihenfolge von der gegebenen Aufgabe abhängt
In den Beispielen 3, 4 und 5 zeigen wir, dass es manchmal keine zwei Wahlmöglichkeiten für die Integrationsreihenfolge gibt, die wir normalerweise bei Doppelintegralen haben.
Das Ziel der Beispiele 3, 4 und 5 ist es, anhand von Grafiken und Diagrammen die Integrationsreihenfolge zu bestimmen, die zur analytischen Berechnung des Doppelintegrals führt.
Beispiel 3
Frage: Berechnen Sie das Doppelintegral \( \displaystyle V = \int _0^1 \int _y^1 (y + e^{-x^2}) \,dx \,dy \), wenn möglich. Kehren Sie die Reihenfolge der Integration um, wenn es notwendig ist, das gegebene Integral zu berechnen.
Lösung zu Beispiel 3
Beginnen wir mit dem inneren Integral:
Sei
\( \displaystyle I = \int _y^1 (y + e^{-x^2}) \,dx \)
Bei dem Versuch, \( I \) zu berechnen, wird schnell klar, dass das Integral \( \displaystyle I = \int _y^1 (e^{-x^2}) \,dx \) nicht analytisch gelöst werden kann.
Gemäß den angegebenen Integrationsgrenzen kann der Integrationsbereich \( R \) des Integrals \( V \) wie folgt beschrieben werden:
\( R \) : \( y \le x \le 1 \) , \( 0 \le y \le 1 \)
Das Diagramm zeigt diesen Bereich als eine Menge horizontaler Streifen.

Lassen Sie uns nun vertikale Streifen verwenden, um den Bereich \( R \) zu beschreiben, wie im untenstehenden Diagramm gezeigt.

Graphen Sie den Bereich \( R \) der Integration, um zu sehen, ob durch Änderung der Integrationsreihenfolge das Integral weiter bearbeitet werden kann.
\( R \) : \( 0 \le x \le 1 \) , \( 0 \le y \le x \)
Das Integral \( V \) kann wie folgt geschrieben werden:
\( \displaystyle V = \int _0^1 \int _0^x (y + e^{-x^2}) \,dy \,dx \)
Berechnen Sie das innere Integral \( I \):
\( \displaystyle I = \int _0^x (y + e^{-x^2}) \,dy \)
\( = \left[ \dfrac{y^2
-------------------------------------------------------------------
}{2} + y \cdot e^{-x^2} \right]_0^x \)
\( = \dfrac{x^2}{2} + x \cdot e^{-x^2} \)
Wir setzen nun \( I \) in \( V \) ein und berechnen das gegebene Integral:
\( \displaystyle V = \int _0^1 \left(\dfrac{x^2}{2} + x \cdot e^{-x^2}\right) dx \)
\( = \left[ \frac{x^3}{6} - \frac{1}{2}e^{-x^2} \right]_0^1 \)
\( = \dfrac{2}{3} - \dfrac{1}{2}e^{-1} \)
Beispiel 4
Frage: Berechnen Sie das Doppelintegral \( \displaystyle V = \iint_R \left(\sqrt{1+y^3} + x \right)\,dy \,dx \) über den Bereich \( R \), der im untenstehenden Diagramm blau schattiert ist.
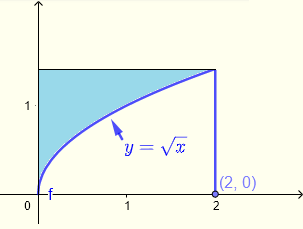
Lösung zu Beispiel 4
Sei das innere Integral \( \displaystyle I = \int \left(\sqrt{1+y^3} + x \right) \,dy \)
Es ist leicht zu erkennen, dass dieses Integral analytisch schwer zu berechnen ist.
Lassen Sie uns die Reihenfolge der Integration ändern:
\( V = \displaystyle \iint_R \left(\sqrt{1+y^3} + x \right)\,dx \,dy \)
Der Bereich \( R \) kann wie folgt beschrieben werden:
\( R\) : \( 0 \le x \le y^2 \) , \( 0 \le y \le \sqrt{2} \)
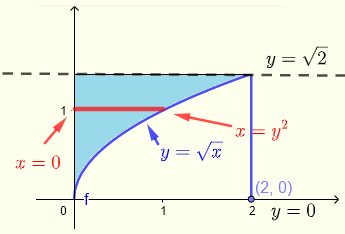
\( \displaystyle V = \int _0^{\sqrt 2} \int _0^{y^2} \left(\sqrt{1+y^3} + x \right) dx dy \)
Berechnen Sie das innere Integral \( I \):
\( I = \displaystyle \int _0^{y^2} \left(\sqrt{1+y^3} + x \right) \,dx \)
\( = \left[ x \cdot \sqrt{1+y^3} + \dfrac{x^2}{2} \right]_0^{y^2} \)
Auswerten und vereinfachen:
\( = y^2 \cdot \sqrt{1+y^3} + \frac{y^4}{2} \)
Setzen Sie \( I \) in \( V \) ein und berechnen Sie das äußere Integral:
\( \displaystyle V = \int _{0\:}^{\sqrt 2} \left(y^2 \cdot \sqrt{1+y^3} + \frac{y^4}{2} \right) \,dy \)
Berechnen Sie das obige Integral:
\( \displaystyle V = \left[ \frac{2}{9}\left(y^3+1\right)^{\frac{3}{2}} + \frac{y^5}{10} \right]_0^{\sqrt 2} \)
Vereinfachen:
\( V = \frac{2}{9}\left(\left(\sqrt{2}\right)^3 + 1\right)^{\frac{3}{2}} + \frac{\left(\sqrt{2}\right)^5}{10} - \dfrac{2}{9} \approx 2.00 \)
Beispiel 5
Frage: Berechnen Sie das Doppelintegral \( \displaystyle V = \iint_R (x+y)\,dy\,dx \) über den Bereich \( R \), der durch die Kurven mit den Gleichungen \( x = (y-2)^2 - 2 \) und \( y = -x + 6 \) begrenzt wird.
Lösung zu Beispiel 5
Wenn vertikale Streifen verwendet werden, hat der Integrationsbereich zwei Teile, da die Grenzen von \( y \) in den Intervallen \( -2 \le x \le 2 \) und \( 2 \le x \le 7 \) unterschiedlich sind, und die Berechnung des Integrals ist sehr anspruchsvoll.
Daher verwenden wir horizontale Streifen.
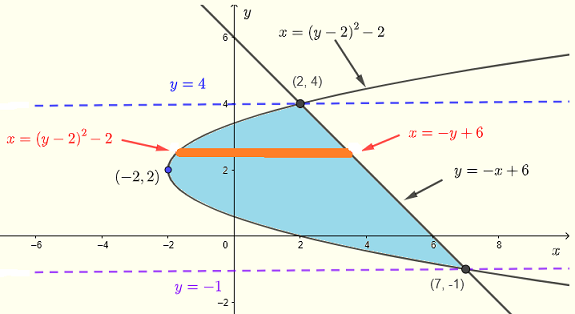
Der Bereich \( R \) kann wie folgt beschrieben werden:
\( R\) : \( (y-2)^2 - 2 \le x \le -y + 6 \) , \( -1 \le y \le 4 \)
\( \displaystyle V = \int _{-1}^{4} \int _{(y-2)^2 - 2}^{-y + 6} (x + y)\,dx \,dy \)
Berechnen Sie das innere Integral \( I \):
\( \displaystyle I = \int _{(y-2)^2 - 2}^{-y + 6} (x + y)\,dx \)
Berechnen Sie das obige Integral:
\( I = \dfrac{-y^4 + 6y^3 - 13y^2 + 12y + 32}{2} \)
Setzen Sie \( I \) in \( V \) ein und berechnen Sie das äußere Integral:
\( \displaystyle V = \int _{-1}^4 \left( \dfrac{-y^4 + 6y^3 - 13y^2 + 12y + 32}{2} \right) \,dy \)
Berechnen Sie das obige Integral:
\( \displaystyle V = \dfrac{1}{2} \left[-\dfrac{y^5}{5} + \dfrac{3y^4}{2} - \dfrac{13y^3}{3} + 6y^2 + 32y \right]_{-1}^4 \)
Auswerten:
\( V = \dfrac{875}{12} \)
Hinweis
Als Übung zeigen Sie, dass das Doppelintegral unter Verwendung von vertikalen Streifen durch folgendes Integral gegeben ist:
\( \displaystyle \int _{-2}^2\:\int _{2-\sqrt{x+2}}^{2+\sqrt{x+2}}\:\left(x+y\right)dy\,dx + \int _2^7\:\int _{2-\sqrt{x+2}}^{-x+6}\:\left(x+y\right)dy\,dx \)
Weitere Fragen mit Antworten
Teil 1
-
Schreiben Sie die Grenzen des Doppelintegrals \( \displaystyle V = \iint_R x \cdot y \,dy \,dx \) und \( \displaystyle V = \iint_R x \cdot y \,dx \,dy \), wobei der Bereich \( R \) in der \( xy\)-Ebene liegt, sodass \(x \ge 0\) und \(y \ge 0\) und durch die Kurve begrenzt wird, deren Gleichung durch
\( x^2 + y^2 = 1 \) gegeben ist, und werten Sie es aus.
-
Schreiben Sie die Grenzen des Doppelintegrals \( \displaystyle V = \iint_R \sin(x^2) \,dy \,dx \) und \( \displaystyle V = \iint_R \sin(x^2) \,dx \,dy \), wobei der Bereich \( R \) ein Dreieck mit den Eckpunkten \( A(0,0)\), \( B(3,0) \) und \( C(3,3) \) ist, und werten Sie es aus.
Teil 2
Werten Sie \( \displaystyle V = \int _0^1 \int _{\arcsin(y)}^{\frac{\pi }{2}}\:(x \cdot y) \,dx\,dy \) aus.
Antworten auf die obigen Fragen
Teil 1:
-
Integrationsbereich:
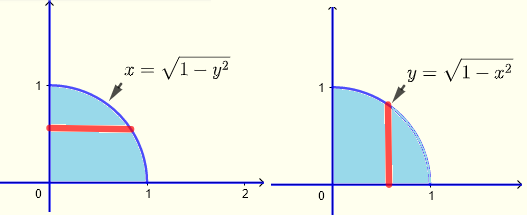
Vertikale Streifen:
\( 0 \le x \le 1 \) , \( 0 \le y \le \sqrt{1-x^2} \)
\( \displaystyle \int _0^1\:\int _0^{\sqrt{1-x^2}}\:xy\:dy\:dx = 1/8 \)
Horizontale Streifen:
\( 0 \le x \le \sqrt{1-y^2} \) , \( 0 \le y \le 1 \)
\( \displaystyle \int _0^1\:\int _0^{\sqrt{1-y^2}}\:xy\:dx\:dy = 1/8\)
-
Integrationsbereich:

Vertikale Streifen:
\( 0 \le x \le 3\) , \( 0 \le y \le x \)
\( \displaystyle \int _0^3\:\int _0^x \:\sin(x^2)\:dy\:dx = \dfrac{1}{2}\left(-\cos \left(9\right)+1\right) \)
Horizontale Streifen:
\( y \le x \le 3 \) , \( 0 \le y \le 3 \)
\( \displaystyle \int _y^3\:\int _0^3\:\sin(x^2)\:dx\:dy \) Sehr schwierig, analytisch zu lösen.
Teil 2:
\( \displaystyle V = \int _0^1 \int _{\arcsin(y)}^{\frac{\pi }{2}}\:(x \cdot y) \,dx\,dy \)
Berechnen Sie das innere Integral \( I \) gegeben durch:
\( \displaystyle I = \int _{\arcsin(y)}^{\frac{\pi }{2}}\:(x \cdot y) \,dx \)
\( = y \cdot \left(\dfrac{\pi^2}{8} - \dfrac{\arcsin^2(y)}{2} \right) \)
Setzen Sie \( I \) in \( V \) ein:
\( \displaystyle V = \int _0^1 \left(y \cdot \left(\dfrac{\pi^2}{8} - \dfrac{\arcsin^2(y)}{2} \right)\right) \,dy \)
was schwierig ist, analytisch zu lösen.
Lassen Sie uns neu beginnen und nun die Integrationsreihenfolge umkehren:
Lassen Sie uns zuerst den Integrationsbereich \( R \) grafisch darstellen:
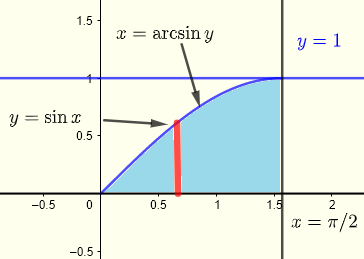
\( \displaystyle V = \int _0^{\frac{\pi }{2}} \int _0^{\sin(x)} x \cdot y \,dy \,dx \)
Berechnen Sie das innere Integral \( I = \int _0^{\sin(x)} x \cdot y \,dy \):
\( I = x \cdot \frac{\sin^2(x)}{2} \)
\( \sin^2(x) = \dfrac{1-\cos(2x)}{2} \)
\( I = \dfrac{x}{4}(1-\cos(2x)) \)
Setzen Sie \( I \) in \( V \) ein:
\( \displaystyle V = \int _0^{\frac{\pi }{2}} \left(\dfrac{x}{4} - \dfrac{x}{4} \cdot \cos(2x)\right) \,dx \)
Teilen Sie den Integranden auf:
\( \displaystyle = \int _0^{\frac{\pi }{2}} \dfrac{x}{4} \,dx - \int _0^{\frac{\pi }{2}} \dfrac{x}{4} \cdot \cos(2x) \,dx \)
Das rechte Integral wird durch die Methode der partiellen Integration berechnet:
\( = \left[ \frac{x^2}{8} \right]_0^{\pi/2} - \left[\frac{1}{8} x \cdot \sin(2x) + \frac{1}{16} \cos(2x) \right]_0^{\pi/2} \)
Auswerten:
\( = \dfrac{\pi^2 + 4}{32} \)
Weitere Referenzen und Links
- Doppelintegral-Berechnungen
- Howard Anton, Irl C. Bivens, Stephen Davis; Calculus: Early Transcendentals; Willey, 2012.
- Gilbert Strang; MIT, Calculus, Wellesley-Cambridge Press, 1991
- Joel Hass, University of California, Davis; Maurice D. Weir, Naval Postgraduate School; George B. Thomas, Jr., Massachusetts Institute of Technology; University Calculus, Early Transcendentals, Third Edition, Boston Columbus, 2016, Pearson.
Ingenieurmathematik mit Beispielen und Lösungen