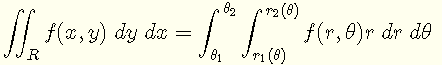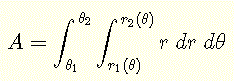Inhaltsverzeichnis
Doppelintegrale in Polarkoordinaten
Beispiele zur Berechnung von Doppelintegralen in Polarkoordinaten und in allgemeinen Integrationsbereichen werden zusammen mit ihren detaillierten Lösungen vorgestellt. Die Beispiele zeigen auch, dass die Umwandlung von Doppelintegralen von kartesischen in Polarkoordinaten die Berechnung mit elementaren Funktionen erleichtern kann.
Umwandlung von Doppelintegralen in Polarkoordinaten
Die Umwandlung von Doppelintegralen von kartesischen (oder rechteckigen) in Polarkoordinaten erfolgt nach [1].
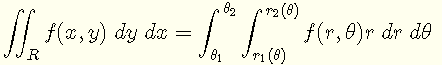
Die Beziehungen zwischen den rechteckigen Koordinaten x und y sowie den Polarkoordinaten r und θ sind gegeben durch [6].
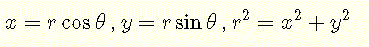
Die Fläche A eines geschlossenen Bereichs R, der in Polarkoordinaten beschrieben wird, ist gegeben durch
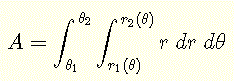
Beispiele mit detaillierten Lösungen
Beispiel 1
\( \) \( \) \( \) \( \)
Frage: Berechnen Sie das Doppelintegral \( \displaystyle V = \iint_R \sqrt {1 - x^2 - y^2} \;dy \;dx \), wobei der Bereich \( R \) die Fläche ist, die von einem Kreis in der \( xy\)-Ebene mit Mittelpunkt im Ursprung und einem Radius von \( 1 \) eingeschlossen wird.
Lösung zu Beispiel 1
Das gegebene Integral ist in rechteckigen Koordinaten und kann nicht mit elementaren Funktionen berechnet werden. Versuchen wir, es in Polarkoordinaten umzuwandeln.
Sei \( f(x,y) = \sqrt {1 - x^2 - y^2} \) und drücken Sie es in Polarkoordinaten aus.
-example-1.gif)
\( r^2 = x^2 + y^2 \)
Daher ist die Funktion \( f(x,y) \) in Polarkoordinaten gegeben durch
\( f(r,\theta) = \sqrt {1 - r^2} \)
Der Integrationsbereich \( R \) ist ein Kreis und kann durch Ungleichungen wie folgt definiert werden:
\( R: \) \( 0 \le \theta \le 2\pi \) und \( 0 \le r \le 1 \)
Das gegebene Integral in rechteckigen Koordinaten kann wie folgt in Polarkoordinaten umgewandelt werden:
\( \displaystyle V = \iint_R \sqrt {1 - x^2 - y^2} \;dy \;dx = \int_0^{2\pi} \int_0^{1} \sqrt{1-r^2} \; r \; dr \; d\theta \)
Sei \( I \) das innere Integral, definiert durch
\( \displaystyle I = \int_0^{1} \sqrt{1-r^2} \; r \; dr \)
\( = \left[ -\frac{1}{3}\left(1-r^2\right)^{\frac{3}{2}} \right]_0^1 = \dfrac{1}{3} \)
Setzen Sie \( I \) ein und berechnen Sie \( V \):
\( \displaystyle V = \int_0^{2\pi} (1/3) \; d\theta \)
\( = \dfrac{1}{3} \left[ \theta \right]_0^{2\pi} \)
\( = \dfrac{2\pi}{3} \)
Beispiel 2
Frage: Berechnen Sie das Doppelintegral \( \displaystyle V = \int_0^{1} \int_0^{\sqrt{1-x^2}} e^{x^2+y^2} \; dy \; dx \).
Lösung zu Beispiel 2
Das gegebene Integral kann in rechteckigen Koordinaten nicht einfach berechnet werden, daher müssen stattdessen Polarkoordinaten verwendet werden, was die Berechnung erleichtern kann.
Drücken wir \( f(x,y) = e^{x^2+y^2} \) in Polarkoordinaten aus.
\( r^2 = x^2 + y^2 \)
Daher ist die Funktion \( f(x,y) \) in Polarkoordinaten gegeben durch
\( f(r,\theta) = e^{r^2} \)
In rechteckigen Koordinaten ist der Integrationsbereich \( R \) durch die gegebenen Integrationsgrenzen definiert.
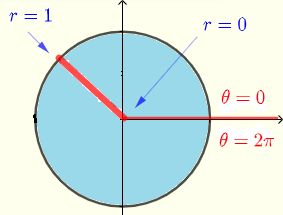
\( R: \) \( 0 \le x \le 1 \) und \( 0 \le y \le \sqrt{1-x^2} \)
Lösen wir die Ungleichung \( y \le \sqrt{1-x^2} \) grafisch.
Quadrieren Sie beide Seiten der Ungleichung:
\( y^2 \le 1-x^2 \)
Schreiben Sie die Terme in \( x \) und \( y \) auf der linken Seite um:
\( y^2 + x^2 \le 1 \)
Die obige Ungleichung beschreibt alle Punkte \( (x,y) \) innerhalb oder auf dem Kreis mit Mittelpunkt im Ursprung \( (0,0) \) und einem Radius von \( 1 \).
Zusammenfassend kann der Integrationsbereich \( R \) wie unten gezeigt beschrieben werden.

Der obige Bereich in Polarkoordinaten wird unten gezeigt.

und ist durch die Ungleichungen definiert:
\( R: \) \( 0 \le \theta \le \pi/2 \) und \( 0 \le r \le 1 \)
Das Integral kann nun in Polarkoordinaten wie folgt umgewandelt werden:
\( \displaystyle V = \int_0^{1} \int_0^{\sqrt{1-x^2}} e^{x^2+y^2} \; dy \; dx = \int_0^{\pi/2} \int_0^1 e^{r^2} r \; dr \; d\theta \)
Sei \( I \) das innere Integral, definiert durch:
\( \displaystyle I = \int_0^1 e^{r^2} r \; dr \)
\( = \left[ \dfrac{1}{2} e^{r^2} \right]_0^1 \)
\( = \dfrac{1}{2} (e - 1) \)
Setzen Sie \( I \) in \( V \) ein:
\( \displaystyle V = \int_0^{\pi/2} \dfrac{1}{2} (e - 1) \; d\theta \)
\( = \dfrac{\pi}{4} (e - 1) \)
Beispiel 3
Frage: Drücken Sie das Integral \( \displaystyle V = \iint_R {x^2+y^2} \; dy \; dx \) aus, wobei \( R \) ein Kreis in der \( xy \)-Ebene mit Mittelpunkt im Punkt \( (1,0) \) und einem Radius von \( 1 \) ist, unter Verwendung von kartesischen (oder rechteckigen) und Polarkoordinaten? Bewerten Sie das Integral.
Lösung zu Beispiel 3
Zuerst zeichnen wir den Integrationsbereich \( R \) und definieren ihn in rechteckigen und Polarkoordinaten.
1) Rechteckige Koordinaten
Die Gleichung des Kreises mit Mittelpunkt im Punkt \( (1,0) \) und einem Radius von \( 1 \) ist gegeben durch:
\( (x-1)^2 + y^2 = 1 \)
Entwickeln Sie die Gleichung und gruppieren Sie die ähnlichen Terme:
\( x^2 - 2x + y^2 = 0 \)
Lösen Sie die obige Gleichung für \( y \), um zwei Lösungen zu erhalten:
\( y = \pm \sqrt {2x-x^2} \)
Unter Verwendung vertikaler Streifen kann der Bereich \( R \) durch die Ungleichungen beschrieben werden:
\( R: \) \( 0 \le x \le 2 \) und \( - \sqrt {2x-x^2} \le y \le \sqrt {2x-x^2} \)
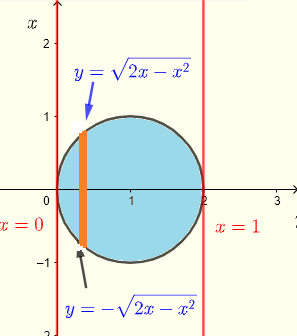
Das Integral kann geschrieben werden als:
\( \displaystyle V = \int_0^2 \int_{-\sqrt {2x-x^2}}^{\sqrt {2x-x^2}} \; \; (x^2+y^2) \; dy \; dx \)
Sei \( I_1 \) das innere Integral, gegeben durch:
\( \displaystyle I_1 = \int_{-\sqrt {2x-x^2}}^{\sqrt {2x-x^2}} \; \; (x^2+y^2) \; dy \)
Bewerten Sie \( I_1 \):
\( \displaystyle I_1 = 2x^2\sqrt{2x-x^2}+2\cdot \frac{\left(2x-x^2\right)^{\frac{3}{2}}}{3} \)
Der nächste Schritt, das äußere Integral in rechteckigen Koordinaten zu berechnen, ist eine Herausforderung.
2) Polarkoordinaten
Verwenden Sie Streifen vom Ursprung zu einem Punkt auf dem Kreis: am Ursprung \( r = 0 \); am Kreis \( r = \sqrt {x^2 + y^2} \).
Lassen Sie uns die Gleichung des Kreises, \( x^2 + y^2 = 2x \), in Polarkoordinaten umwandeln.
Aus der Beziehung zwischen rechteckigen und Polarkoordinaten [6] wissen wir:
\( r^2 = x^2 + y^2 \) und \( x = r \cos \theta \)
Ersetzen Sie \( x^2 + y^2 \) durch \( r^2 \) und \( x \) durch \( r \cos \theta \) in der Gleichung \( x^2 + y^2 = 2x \), um zu erhalten:
\( r^2 = 2 r \cos \theta \)
Teilen Sie beide Seiten der obigen Gleichung durch \( r \):
\( r = 2 \cos \theta \)
In Polarkoordinaten kann der Bereich \( R \) durch die Ungleichungen beschrieben werden:
\( R: \) \( -\pi/2 \le \theta \le \pi/2 \) und \( 0 \le r \le 2 \cos \theta \)

Verwenden Sie \( r^2 = x^2 + y^2 \), um das Integral in Polarkoordinaten umzuschreiben als:
\( \displaystyle V = \int_{-\pi/2}^{\pi/2} \int_{0}^{2 \cos \theta} r^2 \; r \; dr \; d\theta \)
Sei das innere Integral \(I\) definiert durch:
\( \displaystyle I = \int_{0}^{2 \cos \theta} r^2 \; r \; dr \)
Bewerten Sie:
\( \displaystyle I = \left[ r^4 / 4 \right]_{0}^{2 \cos \theta} \)
\( \displaystyle I = 4 cos^4 \theta \) (Gleichung 1)
Reduzieren Sie die Potenz im obigen Ausdruck \( \cos^4 \theta \):
\( \cos^4 \theta = \cos^2 \theta \cos^2 \theta \)
Verwenden Sie die Identität zur Reduzierung der Potenz:
\( \cos^2 \theta = \dfrac{cos (2\theta) + 1}{2} \)
Daher:
\( \cos^4 \theta = \left( \dfrac{\cos (2\theta) + 1}{2} \right)^2 \)
\( = \dfrac{\cos^2(2\theta) + 2 \cos (2\theta) + 1}{4} \)
Verwenden Sie erneut die Identität zur Reduzierung der Potenz:
\( \cos^4 \theta = \dfrac{\cos(4\theta) + 4\cos(2\theta) }{8} + 3/8 \)
Nun setzen Sie den obigen Ausdruck in Gleichung 1 ein, um zu erhalten:
\( I = \dfrac{\cos(4\theta) + 4\cos(2\theta) }{2} + 3/2 \)
Setzen Sie \( I \) in das Integral ein und bewerten Sie:
\( \displaystyle V = \int_{-\pi/2}^{\pi/2} (\dfrac{\cos(4\theta) + 4\cos(2\theta) }{2} + 3/2 ) \; d\theta \)
\( \displaystyle = \left[ \frac{1}{2}\left(\frac{1}{4}\sin \left(4\theta\right)+2\sin \left(2\theta\right)\right)+\frac{3}{2}\theta \right]_{-\pi/2}^{\pi/2} \)
\( = \dfrac{3\pi}{2} \)
Das gegebene Integral ist viel einfacher unter Verwendung von Polarkoordinaten zu bewerten.
Beispiel 4
Frage: Wandeln Sie das Integral \( \displaystyle V = \int_{-1}^0 \int_{-\sqrt{1-x^2}}^0 \dfrac{\sqrt{x^2+y^2}}{1+\sqrt{x^2+y^2}} \; dy \; dx \) in Polarkoordinaten um und bewerten Sie es.
Lösung zu Beispiel 4
Aus den Integrationsgrenzen in rechteckigen Koordinaten schließen wir den Integrationsbereich \( R \), der ein Viertel eines Kreises im dritten Quadranten ist:
\( R: \) \( 0 \le x \le 2 \) und \( - \sqrt {1-x^2} \le y \le 0 \)
und seine Grafik wie unten gezeigt:
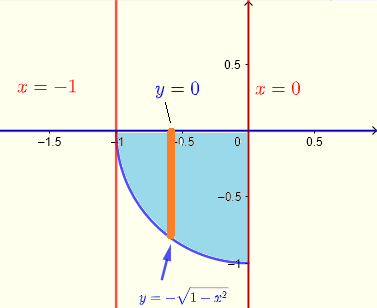
In Polarkoordinaten, unter Verwendung von Streifen vom Ursprung zu einem Punkt auf dem Viertel eines Kreises: am Ursprung \( r = 0 \). Am Kreis \( r = 1 \), kann der Integrationsbereich \( R \) in Polarkoordinaten wie folgt definiert werden:
\( R: \) \( \pi \le \theta \le 3\pi/2 \) und \( 0 \le r \le 1 \)
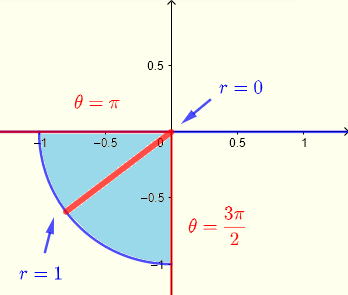
Verwenden Sie \( r = \sqrt { x^2 + y^2 } \), um das gegebene Integral in Polarkoordinaten umzuschreiben:
\( \displaystyle V = \int_{\pi}^{3\pi/2} \int_{0}^{1} \dfrac{r}{1+r} \; r \; dr \; d\theta \)
\( \displaystyle = \int_{\pi}^{3\pi/2} \int_{0}^{1} \dfrac{r^2}{1+r} \; dr \; d\theta \)
Verwenden Sie die Division, um den Integranden \( \dfrac{r^2}{1+r} \) wie folgt zu erweitern:
\( \dfrac{r^2}{1+r} = r-1+\frac{1}{r+1} \)
Setzen Sie den erweiterten Integranden in das Integral ein:
\( \displaystyle V = \int_{\pi}^{3\pi/2} \int_{0}^{1} (r-1+\frac{1}{r+1}) \; dr \; d\theta \)
Integrieren:
\( \displaystyle = \int_{\pi}^{3\pi/2} \left[ \dfrac{r^2}{2} - r + ln |r+1| \right]_0^1 d\theta \)
Bewerten:
\( \displaystyle = \int_{\pi}^{3\pi/2} (\ln (2)-\dfrac{1}{2}) d\theta \)
Integrieren:
\( = \left( \ln (2)-\dfrac{1}{2} \right) \left[ \; \theta \; \right]_{\pi}^{3\pi/2} \)
Bewerten:
\( V = \dfrac{\pi}{2} \left( \ln (2)-\dfrac{1}{2} \right) \)
Mehr Fragen mit Antworten
Teil 1
Wandeln Sie jedes Integral in Polarkoordinaten um und bewerten Sie es.
-
\( \displaystyle V = \int_{-1}^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \; \; \sin(x^2+y^2) \;dy \;dx \)
-
\( \displaystyle V = \int _0^2\:\:\int _0^{\sqrt{4-x^2}} \sqrt{x^2+y^2} \:\;dy\:\;dx\: \)
Teil 2
-
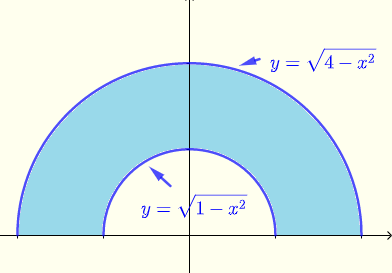
Bewerten Sie \( \displaystyle V = \iint_R \: e^{\sqrt{x^2+y^2}} \; dx \; dy \), wobei \( R \) der im Diagramm unten gezeigte Bereich (blau) ist.
Antworten auf die obigen Fragen
Teil 1:
-
Der Integrationsbereich in rechteckigen (linke Seite) und Polarkoordinaten (rechte Seite) ist unten gezeigt.

\( \displaystyle V = \int_{-1}^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \; \; \sin(x^2+y^2) \;dy \;dx \)
Wandeln Sie das obige Integral in Polarkoordinaten um:
\( \displaystyle V = \int_{0}^{2\pi} \int_0^1 \; \; \sin(r^2) \;r \; dr \;d\theta \)
Bewerten:
\( = \pi (1 -\cos 1) \)
-
Der Integrationsbereich in rechteckigen (linke Seite) und Polarkoordinaten (rechte Seite) ist unten gezeigt.
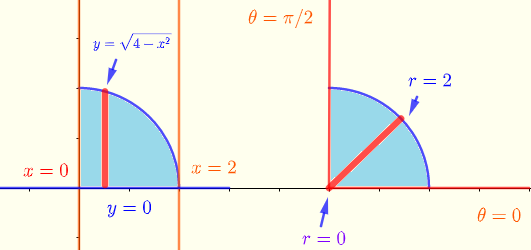
\( \displaystyle V = \int _0^2\:\:\int _0^{\sqrt{4-x^2}} \sqrt{x^2+y^2} \:\;dy\:\;dx\: \)
Wandeln Sie das obige Integral in Polarkoordinaten um:
\( \displaystyle V = \int_{0}^{\pi/2} \int_0^2 \; \; r^2 \; dr \;d\theta \)
Bewerten:
\( = \dfrac{4\pi }{3} \)
Teil 2
Bewerten Sie das gegebene Integral unter Verwendung rechteckiger Koordinaten:
\( \displaystyle V = \int_{-2}^{2} \int_0^{\sqrt{4-x^2}} \: e^{\sqrt{x^2+y^2}} \; dy \; dx - \int_{-1}^{1} \int_0^{\sqrt{1-x^2}} \: e^{\sqrt{x^2+y^2}} \; dy \; dx \)
was mit elementaren Funktionen sehr herausfordernd ist.
Der Integrationsbereich in Polarkoordinaten ist unten gezeigt.
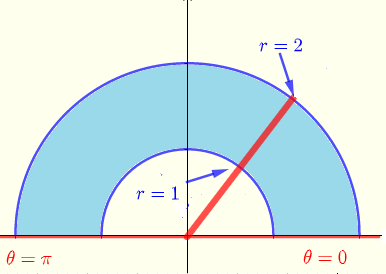
\( R: \) \( 0 \le \theta \le \pi \) und \( 1 \le r \le 2 \)
Gegeben:
\( \displaystyle V = \iint_R \: e^{\sqrt{x^2+y^2}} \; dx \; dy \)
Das gegebene Integral in Polarkoordinaten ist:
\( \displaystyle V = \int_0^{\pi} \; \int_1^2 \: r e^{r} \; dr \; d\theta \)
Bewerten:
\( = \pi e^2 \)
Weitere Referenzen und Links
- Joel Hass, University of California, Davis; Maurice D. Weir, Naval Postgraduate School; George B. Thomas, Jr., Massachusetts Institute of Technology; University Calculus, Early Transcendentals, Third Edition
, Boston Columbus, 2016, Pearson.
- Doppelintegral-Berechnungen
Doppelintegrale über allgemeine Bereiche
- Howard Anton, Irl C. Bivens, Stephen Davis; Calculus: Early Transcendentals; Willey, 2012.
- Gilbert Strang; MIT, Calculus, Wellesley-Cambridge Press, 1991
- Polarkoordinaten
- Umwandlung von Polarkoordinaten in rechteckige Koordinaten und umgekehrt
Technische Mathematik mit Beispielen und Lösungen
-example-1.gif)