Ein interaktiver Online-Grafikrechner zur Visualisierung eines Pulses \( f(t) \) und seiner Fourier-Transformation \( F(\omega) \) wird präsentiert. \( t \) ist die Zeit und \( \omega \) ist die Winkelgeschwindigkeit.
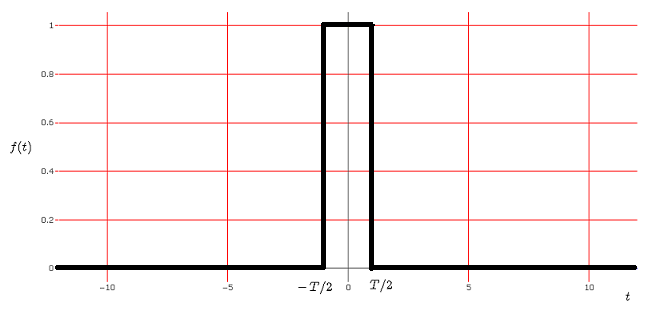Die Fourier-Transformation von \( f(t) \) ist definiert durch:
\[ F(\omega) = \int_{-\infty}^{+\infty} f(t) e^\left( - j \omega t\right) dt \\
= \int_{-T/2}^{+T/2} 1 \cdot e^\left( - j \omega t\right) dt \\
= \left[ \dfrac{ e^\left( - j \omega t \right)}{-j \omega} \right]^{T/2}_{-T/2}
\]
Bewerten und vereinfachen, um zu erhalten:
\[ F(\omega) = \dfrac{\sin(\omega(T/2))}{\omega/2}
\]
T =