AC-Schaltungsprobleme mit Lösungen lösen

Inhaltsverzeichnis

Kirchhoffs und Ohms Gesetz wird erweitert und verwendet, um AC-Schaltungsprobleme unter Verwendung von Impedanzen in komplexen Formen zu lösen.
Alle Größen wie Spannungen, Ströme und Impedanzen werden durch komplexe Zahlen in Standard- und Polarformen dargestellt.

Überblick über komplexe Zahlen

Die imaginäre Einheit wird definiert durch \( j = \sqrt {-1} \) oder \( j^2 = - 1 \)
Eine komplexe Zahl \( Z \) in der Standardform \( Z = a + j b \) kann in Polarform geschrieben werden als
\( Z = r \; \angle \; \theta \)
wobei \( r \) und \( \theta \) der Betrag und das Argument von \( Z \) sind und definiert werden durch
\( r = |Z| = \sqrt {a^2 + b^2} \) und \( \theta = \arctan \left( \dfrac{b}{a} \right) \) im Bereich \( -\pi \lt \theta \le \pi \)
Es ist einfacher, komplexe Zahlen in Polarform zu multiplizieren oder zu dividieren.
Seien \( Z_1 = r_1 \; \angle \; \theta_1 \) und \( Z_2 = r_2 \; \angle \; \theta_2 \)
\( Z_1 \cdot Z_2 = r_1 \cdot r_2 \; \angle \; \theta_1 + \theta_2 \)
\( \dfrac{Z_1}{Z_2} = \dfrac{r_1}{r_2} \; \angle \; \theta_1 - \theta_2 \)

Probleme mit Lösungen

Problem 1
Finden Sie die Amplitude und die Phasenverschiebung (Polarform) des Stroms durch und der Spannungen über den Widerstand \( R \) und den Kondensator \( C \) in der unten dargestellten Schaltung, wobei die Spannungsquelle \( v_i = 10 \cos (\omega t ) \) V, die Widerstände \( R = 100 \; \Omega \), \( C = 0,47 \; \mu F \), die Frequenz \( f = 1 \) kHz und \( \omega = 2 \pi f \) gegeben sind.

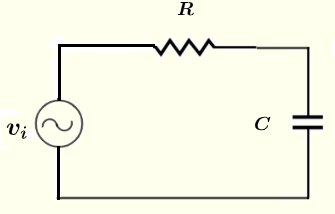
Lösung zu Problem 1
Seien \( V_i \), \( V_R \) \( V_C \) und \( I \) die komplexen Formen von \( v_i \), \( v_R \) \( v_C \) und \( i \) bzw.


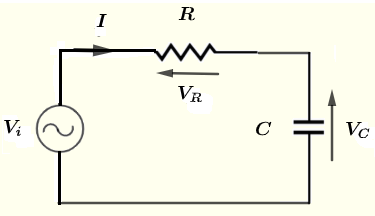
Verwenden Sie das Kirchhoff'sche Spannungsgesetz, um die Gleichung
\( V_i - V_R - V_C = 0\)      (1)
Die komplexen Impedanzen des Widerstands \( R \) und der Kapazität \( C \) sind gegeben durch
\( Z_R = R \; \)       (reell)
\( Z_C = - j \dfrac{1}{\omega C} \; \)       (imaginär)

Verwenden Sie das Ohmsche Gesetz, um
\( V_R = Z_R I \) und \( V_C = Z_C I \) zu schreiben
Ersetzen Sie \( V_R \) und \( V_C \) durch ihren Ausdruck in Gleichung (1)
\( V_i - Z_R I - Z_C I = 0 \)
Lösen Sie die obige Gleichung nach \( I \) auf
\( I = \dfrac{V_i}{Z_R + Z_C} \)

Berechnen Sie \( V_R \) und \( V_C \) mit dem Ohmschen Gesetz wie folgt
\( V_R = Z_R I = \dfrac{V_i Z_R }{Z_R + Z_C} \)

\( V_C = Z_C I = \dfrac{V_i Z_C }{Z_R + Z_C} \)


In komplexer Polarform kann \( v_i = 10 \cos (\omega t ) \) geschrieben werden als
\( V_i = 10 \; \angle \; 0 \)

Nun ersetzen wir \( V_i \), \( Z_R \) und \( Z_C \) durch ihre oben genannten Ausdrücke, um
\( I = \dfrac{10 \; \angle \; 0}{R - j \dfrac{1}{\omega C}} \)

\( V_R = \dfrac{10 R \; \angle \; 0 \; }{R - j \dfrac{1}{\omega C}} \)

\( V_C = \dfrac{ (10 \; \angle \; 0 \;) (- j \dfrac{1}{\omega C}) }{R - j \dfrac{1}{\omega C}} \)

Sei der Nenner in allen obigen Ausdrücken \( Z_D = R - j \dfrac{1}{\omega C} \) und schreiben Sie ihn in komplexer Form
Betrag von \( Z_D \) : \( | Z_D | = \sqrt {R^2 + \dfrac{1}{\omega^2 C^2}} \)

Argument von \( Z_D \) : \( \phi = \arctan \dfrac{-\dfrac{1}{\omega C}}{R} = \arctan \dfrac{-1}{R \omega C} \)

Nun schreiben wir die komplexe Größe \( - j \dfrac{1}{\omega C} \) in Polarform
\( - j \dfrac{1}{\omega C} = \dfrac{1}{\omega C} \; \angle \; -\dfrac{\pi}{2} \)

Nun ersetzen wir alle komplexen Größen in \( I \), \( V_R \) und \( V_C \) durch ihre Polarform und schreiben sie um
\( I = \dfrac{10 \; \angle \; 0}{{ | Z_D | \; \angle \; \phi}} \)

\( V_R = \dfrac{10 R \; \angle \; 0 \; }{ | Z_D | \; \angle \; \phi} \)

\( V_C = \dfrac{10 \; \angle \; 0 \; (\dfrac{1}{\omega C} \; \angle \; -\dfrac{\pi}{2}) }{{ | Z_D | \; \angle \; \phi}} \)

Vereinfachen Sie das oben Gesagte

\( I = \dfrac{10} { | Z_D | } \; \angle \; - \phi \)

\( V_R = \dfrac{10 R}{ | Z_D |} \; \angle \; - \phi \)

\( V_C = \dfrac{10}{ \omega C | Z_D | } \; \angle \; -\dfrac{\pi}{2}- \phi \)

Nun ersetzen wir alle bekannten Größen durch ihre numerischen Werte
\( \omega = 2 \cdot \pi \cdot f = 2 \cdot \pi 10^3 = 2000 \pi \)
\( | Z_D | = \sqrt {R^2 + \dfrac{1}{\omega^2 C^2}} = \sqrt {100^2 + \dfrac{1}{(2000 \pi)^2 (0,47 \cdot 10^{-6})^2}} = 353,08 \; \Omega \)
\( \phi = \arctan \dfrac{-\dfrac{1}{\omega C}}{R} = \arctan \dfrac{-\dfrac{1}{2000 \pi \cdot 0,47 \cdot 10^{-6} }}{100} = -73,55^{\circ} \)
Daher

\( I = \dfrac{10} { | Z_D | } \; \angle \; - \phi = 0,0283 \; \angle \; 73,55^{\circ} \)
Betrag von \( I \) ist \( 0,02832 \; A\) und die Phasenverschiebung ist \( 73,55^{\circ} \)

\( V_R = \dfrac{10 R}{ | Z_D |} \; \angle \; - \phi = 2,832 \; \angle \; 73,55^{\circ} \)
Betrag von \( V_R \) ist \( 2,832 \; V\) und die Phasenverschiebung ist \( 73,55^{\circ} \)

\( V_C = \dfrac{10}{ \omega C | Z_D | } \; \angle \; -\dfrac{\pi}{2}- \phi = 9,591 \; \angle \; -16,45^{\circ} \)
Betrag von \( V_C \) ist \( 9,591 \; V\) und die Phasenverschiebung ist \( -16,45^{\circ} \)

Problem 2

Finden Sie die Amplitude und die Phasenverschiebung (Polarform) der Spannung \( v_o \) in der unten dargestellten Schaltung, wobei die Spannungsquelle \( v_i = 10 \cos (\omega t ) \; V \), die Widerstände \( R = 100 \; \Omega \), \( C = 0,47 \; \mu F \), \( L = 300 \; mH \), die Frequenz \( f = 2 \) kHz und \( \omega = 2 \pi f \) gegeben sind.


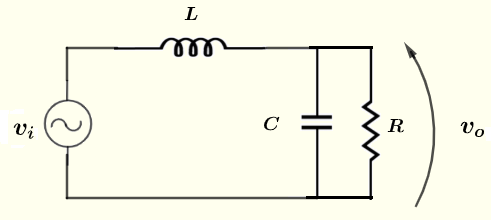
Lösung zu Problem 2
Seien \( I \), \( V_i \) und \( V_0 \) die komplexen Formen von \( i \), \( v_i \) und \( v_o \) bzw.
\( V_i \) kann in Polarform wie folgt geschrieben werden
\( V_i = 10 \; \angle \; 0 \)
Die Impedanz des Widerstands \( R \) ist gegeben durch
\( Z_R = R \; \)
Die Impedanz des Kondensators \( C \) ist gegeben durch
\( Z_C = - j \dfrac{1}{\omega C} \; \)
Der Widerstand \( R \) und der Kondensator \( C \) sind parallel geschaltet. Die Impedanz \( Z \), die \( R \) und \( C \) äquivalent ist, ist gegeben durch

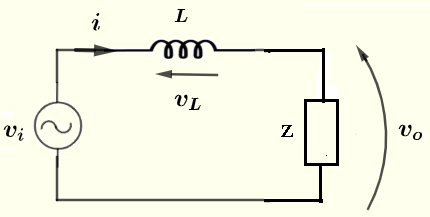
\( Z = \dfrac{Z_R \cdot Z_C}{Z_R + Z_C} \)
Die Impedanz der Induktivität \( L \) ist gegeben durch \( Z_L \)
\( Z_L = j \omega L \)
Verwenden Sie das Kirchhoff'sche Spannungsgesetz, um die Gleichung
\( V_i - V_L - V_0 = 0\)      (1)
Verwenden Sie das Ohmsche Gesetz, um
\( V_L = Z_L I \) und \( V_0 = Z I \) zu schreiben
Ersetzen Sie \( V_L \) und \( V_0 \) durch ihren Ausdruck in Gleichung (1)
\( V_i - Z_L I - Z I = 0 \)
Lösen Sie für \( I \)
\( I = \dfrac{V_i}{ Z_L + Z} \)
Verwenden Sie das Ohmsche Gesetz, um
\( V_o = Z I = \dfrac{Z}{ Z_L + Z} V_i\)
Ersetzen Sie durch bekannte Größen, um numerische Werte zu finden
\( \omega = 2 \pi f = 2 \pi \cdot 2000 = 4000 \pi \)
\( Z_R = R = 100 \)
\( Z_C = - j \dfrac{1}{\omega C} = - j \dfrac{1}{4000 \pi \cdot 0,47 \cdot 10^{-6}} = - 169,314 j \)

\( Z = \dfrac{R \cdot Z_C}{R + Z_C} \) ( (\( R \) und \( C \) in Parallelschaltung )

\( = \dfrac{100 \cdot (- 169,314 j)}{100 - 169,314 j } = 74,138 -43,787 j\)
und
\( Z_L = j \omega L = 4000 \pi \cdot 300 \cdot 10^{-3} j = 3769,911 j \)
\( V_o = \dfrac{Z}{ Z_L + Z} V_i \)

\( = \dfrac{Z}{ Z_L + Z} V_i \)

\( = \dfrac{74,138 -43,787 j}{ 3769,911 j + 74,138 -43,787 j} V_i \)
Vereinfachen
\( = (-0,01135 -0,02012 j) V_i \)
Schreiben Sie die komplexe Zahl \( (-0,01135 -0,02012 j) \) in Polarform und setzen Sie \( V_i \) durch ihre Werte in Polarform, die oben angegeben sind.
\( = ( 0,02310 \angle -119,43^{\circ} ) (10 \; \angle \; 0) \)
Vereinfachen
\( V_o = 0,23 \; \angle \; -119,43^{\circ} \)

Problem 3

Finden Sie die Amplitude und die Phasenverschiebung (Polarform) der Spannung \( v_o \) in der unten dargestellten Schaltung, wobei die Spannungsquelle \( v_i = 10 \cos (\omega t ) \; V \), die Widerstände \( R_1 = 220 \; \Omega \), \( R_2 = 2,2 \; k\Omega \), \( R_3 = 1 \; k\Omega \), \( C_1 = 0,47 \; \mu F \), \( C_2 = 1,5 \; \mu F \), \( L = 30\; mH \), die Frequenz \( f = 2,5 \) kHz und \( \omega = 2 \pi f \) gegeben sind.

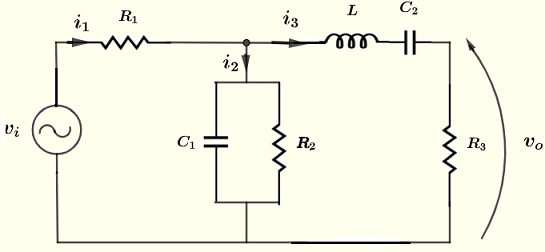
Lösung zu Beispiel 3
Seien \( I_1 \), \( I_2 \), \( I_3 \), \( V_i \) und \( V_0 \) die komplexen Formen von \( i_1 \), \( i_2 \), \( i_3 \), \( v_i \) und \( v_o \) bzw.
\( V_i \) kann in Polarform wie folgt geschrieben werden
\( V_i = 10 \; \angle \; 0 \)
\( V_o \) kann unter Verwendung des Ohmschen Gesetzes berechnet werden
\( V_o = R_3 I_3\)
Daher müssen wir \( I_3 \) berechnen
Lassen Sie uns die Impedanzen gruppieren, wie in der unten gezeigten Schaltung, so dass
\( Z_1 = R_1 \)
\( Z_2 = \dfrac{R_2 ( - \dfrac{1}{\omega C_1} j)}{R_2 - \dfrac{1}{\omega C_1} j} \)      ( \( C_1 \) und \( R_2 \) sind in Parallelschaltung)
\( z_3 = R_3 + j \omega L - \dfrac{1}{ \omega C_2} j \)      ( \( C_2 \), \( L \) und \( R_3 \) sind in Reihenschaltung)

Das Kirchhoff'sche Spannungsgesetz, angewendet auf die beiden geschlossenen Schleifen, ergibt 2 Gleichungen
\( V_i - V_{z_1} - V_{z_2} = 0 \)
\( V_{z_2} - V_{z_3} = 0 \)
Verwenden Sie das Ohmsche Gesetz, um \( V_{z_1} = Z_1 I_1 \), \( V_{z_2} = Z_2 I_2 \) und \( V_{z_3} = Z_3 I_3 \) zu schreiben und setzen Sie in die obigen Gleichungen ein, um Gleichungen nur mit Strömen zu erhalten.
\( V_i - Z_1 I_1 - Z_2 I_2 = 0 \)     (1)
\( Z_2 I_2 - Z_3 I_3 = 0 \)     (2)
Nun verwenden wir das Kirchhoff'sche Stromgesetz am Knotenpunkt A, um zu schreiben
\( I_1 = I_2 + I_3 \)     (3)
Wir haben 3 Gleichungen mit drei Unbekannten \( I_1 \), \( I_2 \) und \( I_3 \), aber wir benötigen nur \( I_3 \).
Verwenden Sie Gleichung (3), um \( I_1 \) in Gleichung (1) durch \( I_2 + I_3 \) zu ersetzen und so \( I_1 \) aus den Gleichungen zu eliminieren und am Ende ein System von zwei Gleichungen und zwei Unbekannten zu erhalten.
\( V_i - Z_1 ( I_2 + I_3) - Z_2 I_2 = 0 \)     (4)
\( Z_2 I_2 - Z_3 I_3 = 0 \)     (5)
Schreiben Sie das obige Gleichungssystem in Standardform
\( (Z_1 + Z_2 ) I_2 + Z_1 I_3 = V_i \)     (4)
\( Z_2 I_2 - Z_3 I_3 = 0 \)     (5)
Verwenden Sie Determinanten, um das obige Gleichungssystem zu lösen
\( I_3 = \dfrac{\begin{vmatrix} Z_1 + Z_2 & V_i \\ Z_2 & 0 \end{vmatrix}}{\begin{vmatrix} Z_1 + Z_2 & + Z_1 \\ Z_2 & -Z_3 \end{vmatrix}} \)
Bewerten Sie die Determinanten, um zu finden
\( I_3 = \dfrac{Z_2}{(Z_1+Z_2)Z_3 + Z_1 Z_2} V_i \)

Numerische Berechnungen
\( \omega = 2 \pi f = 5000 \pi \)
\( Z_1 = 220 \)
\( Z_2 = \dfrac{2200 ( - \dfrac{1}{5000 \pi \cdot 0,47 10^{-6}} j)}{2200 - \dfrac{1}{5000 \pi \cdot 0,47 10^{-6}} j} \)

\( Z_2 = 8,30804 -134,93950 j \)

\( z_3 = 1000 + 5000 \pi \cdot 30 \cdot 10^{-3} j - \dfrac{1}{ 5000 \pi \cdot 1,5 \cdot 10^{-6}} j \)
\( Z_3 = 1000 + 428,79757 j \)
\( I_3 = (0,00013 - 0,00043 j)V_i = 0,00044 \angle -73,18^{\circ} \cdot 10 \angle 0\)
\( V_0 = R_3 I_3 = 1000 \cdot 0,00044 \angle -73,18^{\circ} \cdot 10 \angle 0 \)
Vereinfachen
\( V_0 = 4,4 \angle -73,18^{\circ} V \)

Weitere Probleme mit Antworten

Problem 4
Gegeben ist \( v_i = 10 \angle 0^{\circ} \), \( R = 200 \; \Omega \), \( C = 0,47 \; \mu F \), \( L = 40 \; mH \), Frequenz \( f = 1 \) kHz.
Finden Sie den Strom \( I \) durch und die Spannung \( V_0 \) über der Induktivität in komplexer Form.

Antwort zu Problem 4

Antwort: \( I = 0,047 \angle -47,84^{\circ}\), \(V_0 = 11,38 \angle 42,16^{\circ} \)

Problem 5
Gegeben ist \( v_i = 10 \angle 0^{\circ} \), \( R_1 = 100 \; \Omega \), \( C = 0,47 \; \mu F \), \( R_2 = 120 \; \Omega \), \( R_3 = 200 \; \Omega \), \( R_4 = 400 \; \Omega \), \( L = 20 \; mH \), Frequenz \( f = 2 \) kHz.
Finden Sie die Ströme \( I_1 \), \( I_2 \), \( I_3 \) und die Spannungen über jedem Widerstand in komplexer Form.

Antwort zu Problem 5
Antworten:
Ströme: \( I_1 = 0,054 \angle 10,55^{\circ} \; , \; I_2 = 0,048 \angle 23,01^{\circ} \; , \; I_3 = 0,013 \angle -42,22^{\circ} \)
Spannungen: \( V_{R_1} = 5,49 \angle 10,55^{\circ} \; , \; V_{R_2} = 4,71 \angle -12,32^{\circ} \; , \; V_{R_3} = 2,60 \angle -42,22^{\circ} \; , \; V_{R_4} = 2,77 \angle 15,63^{\circ} \)

Weitere Referenzen und Links