Resonanz-Serienschaltung RLC

Inhaltsverzeichnis

Resonante RLC-Serienschaltungen und Formeln für die Resonanzfrequenz , die Grenzfrequenzen , die Bandbreite und den Gütefaktor werden entwickelt und mit Beispielen und detaillierten Lösungen dargestellt. \( \) \( \) \( \) \( \)
Im Folgenden ist der Großbuchstabe \( I \) die komplexe (polare) Form des realen Stroms \( i \) und der Großbuchstabe \( V_i \) die komplexe (polare) Form der realen Spannung \( v_i \).
Ein Resonanz-Serienschaltung RLC-Rechner kann verwendet werden, um die Berechnungen der untenstehenden Beispiele zu überprüfen und auch für weitere Übungen und Untersuchungen dieser Schaltungen.

A - Resonanz-Serienschaltung RLC

Betrachten Sie die unten dargestellte Serienschaltung RLC.

Für eine Schaltung, die von einer Spannungsquelle mit der Frequenz \( f \) versorgt wird, wird die Gesamtimpedanz \( Z \) der Serienschaltung RLC wie folgt gegeben:
\[ Z = R + j \left(\omega L - \dfrac{1}{\omega C} \right) \]
Die Beziehung zwischen dem Strom \( I \) und der Spannung \( V_i \) wird durch
\[ I = \dfrac{V_i}{Z} \]
gegeben, wobei \( V_i \) und \( I \) die komplexe Form der Spannung \( v_i \) bzw. des Stroms \( i \) sind.
Verwendet man die Definition des Betrags einer komplexen Zahl, so wird der Betrag \( |Z| \) durch
\( |Z| = \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} \)
Wenn \( V_0 \) der Spitzenwert der Spannungsquelle \( v_i = V_0 \cos (\omega t) \) ist, dann wird der Spitzenwert \( I_0 \) von \( I \) durch
\( I_0 = \dfrac{V_0}{ |Z| } = \dfrac{V_0}{ \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} } \)
Die Resonanzfrequenz wird definiert als die Frequenz, bei der \( I_0 \) maximal ist oder wenn der Betrag von \( Z \) minimal ist.
Da der Widerstand \( R \) unabhängig von der Frequenz ist, tritt der minimale Wert von \( |Z| \) bei \( \omega = \omega_r \) auf, sodass
\( \left(\omega_r L - \dfrac{1}{\omega_r C} \right) = 0 \)
Lösen Sie das Obige nach \( \omega_r \) auf, um die Resonanzfrequenz zu erhalten
\[ \omega_r = \dfrac{1}{\sqrt {L C}} \quad \quad (I) \]
Bei der Resonanzfrequenz \( \omega = \omega_r \), haben wir:
1) \( Z = R \)
Für \( V_0 \), den Spitzenwert der Spannungsquelle \( v_i \), wird der Spitzenwert \( I_0 \) von \( I \) durch
2) \( I_0 = \dfrac{V_0}{R} \)
gegeben.
Setzen Sie \( X_L = \omega L \) und \( X_C = \dfrac{1}{\omega C} \)
3) \( X_L = X_C \)

Beispiel 1
Gegeben: \( R=300 \; \Omega \), \( L = 100 \; mH \) und \( C = 100 \mu F \) in der obigen Serienschaltung RLC.
a) Bestimmen Sie die Resonanzfrequenz \( \omega_r \)
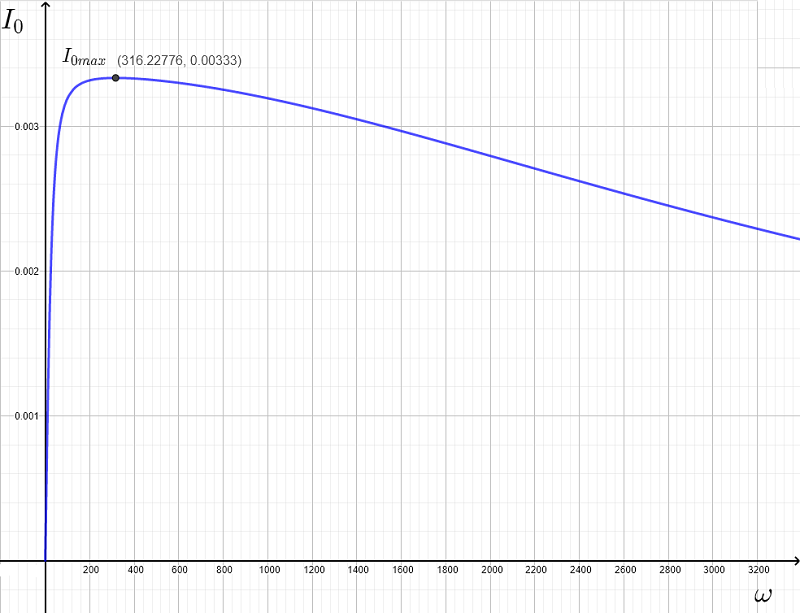
b) Zeichnen Sie die Graphen von \( |Z| \), \( X_L = \omega L \), \( X_C = \dfrac{1}{\omega C} \) und \( I_0 \) als Funktion der Frequenz \( \omega \) und diskutieren Sie die erhaltenen Graphen.

Lösung für Beispiel 1
a)
Die Resonanzfrequenz \( \omega_r \) wird durch
\( \omega_r = \dfrac{1}{\sqrt {L C}} = \dfrac{1}{\sqrt{100\times10^{-3} \times 100 \times 10^{-6}}} \approx 316,23\)
gegeben. b)
Nachfolgend werden die Graphen von \( |Z| \), \( X_L \) und \( X_C \) dargestellt.
Aus den Graphen hat \( |Z| \) einen minimalen Wert von \( R = 300 \; \Omega \) (Punkt A).
Die Graphen von \( X_L \) und \( X_C \) schneiden sich (Punkt B) und daher ist \( X_L = X_C \) oder \( \left(\omega_r L - \dfrac{1}{\omega_r C} \right) = 0 \).



Im unten stehenden Diagramm ist der Strom \( I_0 \) dargestellt, der bei der Resonanzfrequenz \( \omega_r \approx 316,23\) (nach Rundung auf 2 Dezimalstellen) maximal ist.

B - Durchschnittsleistung in einem Resonanzkreis

Die Durchschnittsleistung \( P_a \), die der Serienschaltung RLC geliefert wird, wird durch: \[ \displaystyle \quad \quad P_a = \dfrac{V_0^2}{2 |Z|} \cos \theta \quad \quad (II) \] gegeben, wobei \( \theta \) das Argument der Impedanz \( Z = R + j \left(\omega L - \dfrac{1}{\omega C} \right) \) ist und wie folgt gegeben wird:
\( \theta = \arctan \left( \dfrac{ \omega L - \dfrac{1}{\omega C} }{R} \right) \)
Verwenden Sie die Eigenschaften der Umkehrtrigonometrie, erhalten wir
\( \tan \theta = \left( \dfrac{ \omega L - \dfrac{1}{\omega C} }{R} \right) \)
\( \theta \) kann als spitzer Winkel eines rechtwinkligen Dreiecks angenommen werden, wie unten gezeigt. (Verwenden Sie die Definition des Tangens eines Winkels in einem rechtwinkligen Dreieck und sehen Sie, dass Sie \( \tan \theta \) wie oben definiert erhalten können.)



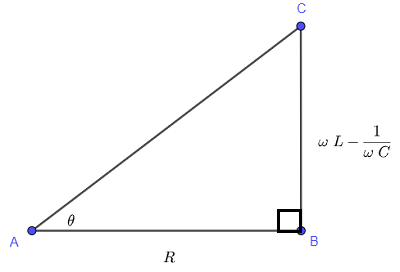
Wir verwenden nun dasselbe Dreieck und berechnen den Leistungsfaktor \( \cos \theta \)
Die Hypotenuse des Dreiecks wird wie folgt berechnet
\( AC = \sqrt {R^2 + \left( \omega L - \dfrac{1}{\omega C} \right)^2} \)
\( \cos \theta = \dfrac{AB}{AC} = \dfrac{R}{\sqrt {R^2 + \left( \omega L - \dfrac{1}{\omega C} \right)^2}} \)
Setzen Sie \( \cos \theta \) und \( |Z| \) in die obige Formel (II) ein und drücken Sie die Leistung \( P_a \) wie folgt aus:
\( \displaystyle \quad \quad P_a = \dfrac{V_0^2}{2 \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} }\dfrac{R}{\sqrt {R^2 + \left( \omega L - \dfrac{1}{\omega C} \right)^2}} \)
Vereinfachen Sie dies:
\[ \displaystyle \quad \quad P_a = \dfrac{V_0^2 R}{2 \left({R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} \right) } \quad \quad (III) \]
Bei der Resonanzfrequenz \( \omega_r = \dfrac{1}{\sqrt {LC}} \), haben wir \( \left(\omega_r L - \dfrac{1}{\omega_r C} \right) = 0 \) und daher ist die Leistung maximal und gleich \[ P_{a max} = \dfrac{V_0^2}{2 \; R} \quad \quad (IV) \]

C - Grenzfrequenzen eines Resonanzkreises und der Gütefaktor

Wir definieren nun die Grenzfrequenzen als die Frequenzen \( \omega_c \), bei denen die Leistung \( P_a(\omega) \) in (III) halb so groß wie die maximale Leistung \( P_{a max} \) in (IV) ist.
Daher müssen wir die Gleichung lösen
\( P_a (\omega_c ) = \dfrac{1}{2} \left(\dfrac{V_0^2}{2 \; R} \right) \)

\( \dfrac{V_0^2 R}{2 \left({R^2 + \left(\omega_c L - \dfrac{1}{\omega_c C} \right)^2} \right) } = \dfrac{1}{2} \dfrac{V_0^2}{2 \; R} \)
Vereinfachen Sie zu
\( \dfrac{ R}{2 \left({R^2 + \left(\omega_c L - \dfrac{1}{\omega_c C} \right)^2} \right) } = \dfrac{1}{4 R} \)
Multiplizieren Sie über Kreuz, vereinfachen Sie und schreiben Sie die obige Gleichung wie folgt um
\( (\omega_c L - \dfrac {1}{\omega_c C } ) = R^2 \)
Lösen Sie durch das Extrahieren der Quadratwurzel, um zwei Gleichungen zu erhalten
\( \omega_c L - \dfrac {1}{\omega_c C} = \pm R \)
Multiplizieren Sie alle Terme mit \( \omega_c C \) und vereinfachen Sie
\( \omega_c^2 L C - 1 = \pm \omega_c R C \)
Schreiben Sie es als quadratische Gleichungen in Standardformen um
\( \omega_c^2 L C \pm \omega_c R C - 1 = 0\)
Lösen Sie die erste quadratische Gleichung \( \quad \omega_c^2 L C + \omega_c R C - 1 = 0\)
um zwei Lösungen zu erhalten
\( \omega_{c1} = \dfrac {- R C \pm \sqrt{ (R C)^2 + 4 L C }}{ 2 L C } \)

Lösen Sie die zweite quadratische Gleichung \( \quad \omega_c^2 L C - \omega_c R C - 1=0\)
um zwei Lösungen zu erhalten
\( \omega_{c2} = \dfrac {R C \pm \sqrt{ (R C)^2 + 4 L C}}{ 2 L C } \)
Wir haben insgesamt 4 Lösungen. Beachten Sie, dass die Größe \( \sqrt{ (R C)^2 + 4 L C } \) größer ist als \( RC \) und daher nur zwei Lösungen gültig sind, da die Grenzfrequenz eine positive Größe ist.
Die Grenzfrequenzen \( \omega_{c1} \) und \( \omega_{c2} \) sind die beiden gegebenen Lösungen:
\( \omega_{c1} = \dfrac {- R C + \sqrt{ (R C)^2 + 4 L C }}{ 2 L C } \)

\( \omega_{c2} = \dfrac {R C + \sqrt{ (R C)^2 + 4 L C}}{ 2 L C } \)
Wir haben bereits die Resonanzfrequenz \( \omega_r = \dfrac{1}{\sqrt{LC}} \) gefunden.
Verwenden Sie einfache Algebra, um \( \omega_{c1} \) und \( \omega_{c2} \) in Bezug auf \( \omega_r \) umzuschreiben
\[ \omega_{c1} = - \dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} \quad \quad (V) \]
\[ \omega_{c2} = \dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} \quad \quad (VI) \]

Hinweis: Beachten Sie, dass
\[ \omega_{c1} \times \omega_{c2} = \omega_r^2 \quad \quad (VII) \]

Die Bandbreite des Resonanzkreises wird definiert als: \( \Delta \omega = \omega_{c2} - \omega_{c1} \)

Der Gütefaktor \( Q \) wird definiert als:
\( Q = \dfrac{\omega_r}{\Delta \omega} \)
Setzen Sie ein:
\( Q = \dfrac {\omega_r} { \left(\dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} - \left(-\dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} \right) \right)} \)
Vereinfachen Sie dies:
\[ Q = \omega_r \dfrac{L}{R} \quad \quad (VIII) \]

D - Weitere Beispiele mit detaillierten Lösungen

Beispiel 3
Eine Resonanzschaltung RLC soll so konstruiert werden, dass sie die Frequenzen \( f_{c_1} = 650 \) Hertz und \( f_{c_2} = 950 \) Hertz als untere und obere Grenzfrequenzen hat.
a) Berechnen Sie die Kapazität des Kondensators \( C \) und die Induktivität der Spule \( L \), wenn der Widerstand des Widerstands \( R \) \( 30 \Omega \) beträgt.
b) Wie hoch ist der Gütefaktor der Schaltung?

Lösung für Beispiel 3
a)
Berechnen Sie die Kreisfrequenzen.
\( \omega_{c_1} = 2 \pi f_{c_1} = 1300 \pi \) rad/s
\( \omega_{c_2} = 2 \pi f_{c_2} = 1900 \pi \) rad/s
Verwenden Sie die oben entwickelte Formel (VII)
\( \omega_{c_1} \times \omega_{c_2} = \omega_{r}^2 \) um die Resonanzfrequenz \( \omega_{r} \) der Schaltung zu berechnen.
\( \omega_{r} = \sqrt {\omega_{c_1} \times \omega_{c_2}} = \sqrt {1300 \pi \times 1900 \pi } = 100 \sqrt{247} \pi = 4937,400 \) rad/s
\( \omega_{c_2} - \omega_{c_1} = \dfrac{R}{L} \)
Daher
\( L = \dfrac{R } {\omega_{c_2} - \omega_{c_1}} = \dfrac{30} {1900 \pi - 1300 \pi } = 0,01591 \) H
\( \omega_{r} = \dfrac{1}{\sqrt {L C} } \)
Daher
\( C = \dfrac{1}{\omega_{r}^2 L} = \dfrac{1}{(100 \sqrt{247} \pi)^2 \times 0,01591} = 2,5783 \times 10^{-6} \) F

b)
Der Gütefaktor wird durch
\( Q = \dfrac{\omega_{r}}{\omega_{c_2} - \omega_{c_1}} = \dfrac{100 \sqrt{247} \pi}{1900 \pi - 1300 \pi } = 2,62\)

Weitere Referenzen und Links

• Resonanz-Serienschaltung RLC Rechner
• RLC-Serienschaltungen
• Serienschaltung RLC Impedanzrechner
• Parallelschaltung RLC Impedanzrechner
• RLC Serienschaltung Strom-Graphing Rechner