Strom- und Spannungsermittlung im Serien-RLC-Schaltkreis

Inhaltsverzeichnis

Hier wird erläutert, wie komplexe Impedanzen verwendet werden, um Ströme und Spannungen in Serien-RLC-Schaltkreisen zu analysieren. Komplexe Zahlen vereinfachen die Berechnungen von Impedanzen, Strömen und Spannungen in Wechselstromkreisen erheblich.
Da das Symbol \( i \) für Ströme in Wechselstromkreisen verwendet wird, verwenden wir hier \( j \) als imaginäre Einheit, definiert durch \( j^2 = -1 \) oder \( j = \sqrt{-1} \).
Kleinbuchstaben für Strom und Spannungen werden für reale Größen verwendet. Großbuchstaben für Strom und Spannungen werden für komplexe Größen in Polardarstellung verwendet.

A - Impedanzen als Komplexe Zahlen und Phasoren eines Serien-RLC-Schaltkreises

Für einen Schaltkreis, der von einer Spannungsquelle mit der Frequenz \( f \) gespeist wird, werden die Impedanzen der verschiedenen RLC-Komponenten wie folgt angegeben:
Die Impedanz in komplexer Form \( Z_R \) eines Widerstands mit dem Widerstand \( R \) ist gegeben durch \[ Z_R = R \] Die Impedanz in komplexer Form \( Z_L \) einer Induktivität mit der Induktivität \( L \), auch als induktiver Blindwiderstand bezeichnet, ist gegeben durch \[ Z_L = j \omega L \] Die Impedanz in komplexer Form \( Z_C \) eines Kondensators mit der Kapazität \( C \), auch als kapazitiver Blindwiderstand bezeichnet, ist gegeben durch \[ Z_C = - \dfrac{1}{\omega C} j \] wobei \( \omega = 2 \pi f \)
Das Wichtigste ist zu beachten, dass die induktiven und kapazitiven Blindwiderstände von der Frequenz der Spannungsquelle abhängen.

Seien \( V_i \), \( I \), \( V_R \), \( V_L \) und \( V_C \) die komplexen Formen von \( v_i \), \( i \), \( v_R \), \( v_L \) und \( v_C \).
Wenden Sie das Kirchhoff'sche Gesetz für Spannungen, erweitert auf komplexe Impedanzen, an, um zu schreiben
\( V_i - V_R - V_L - V_C = 0\)     (1)
Wenden Sie das Ohmsche Gesetz, erweitert auf komplexe Impedanzen, an, um zu schreiben
\( V_R = Z_R I \)
\( V_L = Z_L I \)
\( V_C = Z_C I \)
Setzen Sie das Obige in Gleichung (1) ein, um zu erhalten
\( V_i = Z_R I + Z_L I + Z_C I = 0\)
Lösen Sie das Obige für \( I \)
\( I = \dfrac{V_i}{Z_R + Z_L + Z_C } \)
Sei \( Z \) die äquivalente komplexe Impedanz des Serien-RLC-Schaltkreises, definiert als
\[ Z = Z_R + Z_L + Z_C = R + j \left(\omega L - \dfrac{1}{\omega C} \right) \]
Der Betrag von \( Z \): \[ |Z| = \sqrt{R^2 + \left(\omega L - \dfrac{1}{\omega C}\right)^2} \]
Das Argument von \( Z \): \[ \theta = \arctan \left( \dfrac {\omega L - \dfrac{1}{\omega C}}{R} \right) \]
Beachten Sie, dass sowohl der Betrag als auch das Argument der Impedanz \( Z \) von der Frequenz (\( \omega = 2 \pi f \)) der Spannungsquelle abhängen. Diese Eigenschaft ist nützlich bei der Konstruktion von Filtern und hat viele andere Anwendungen in elektronischen Schaltkreisen.
Schreiben Sie \( Z \) in Polardarstellung
\[ Z = |Z| \; \angle \; \theta \]
Die Ausdrücke für \( Z_R, Z_L, Z_C \) und \( Z \), wie oben angegeben, könnten geometrisch unter Verwendung von Phasoren interpretiert werden, wie unten gezeigt.


In Teil (a) werden \( Z_R, Z_L\) und \( Z_C \) in einem Achsensystem mit dem Realteil entlang der Horizontalen und dem Imaginärteil entlang der Vertikalen dargestellt.
In Teil (b) wird \( Z = Z_R + Z_L + Z_C \) geometrisch unter Verwendung der Vektoraddition (oder der Addition komplexer Zahlen) dargestellt.
In Teil (c) ein rechtwinkliges Dreieck mit Hypotenuse, die den Betrag von \( Z \) darstellt: unter Verwendung des Satzes des Pythagoras: \( |Z| = \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C}\right)^2} \), genau wie oben unter Verwendung komplexer Zahlen erhalten.
Wiederum unter Verwendung des rechtwinkligen Dreiecks: Winkel \( \theta = \arctan \left (\dfrac{\omega L - \dfrac{1}{\omega C}}{R} \right) \)

B - Strom und Spannungen in einem Serien-RLC-Schaltkreis

Sei \( v_i = V_0 \cos (\omega t) \) , \( V_0 \) der Spitzenwert der Spannungsquelle.
Euler'sche Formel für komplexe Zahlen:
\( e^{j \omega t} = \cos (\omega t) + j \sin (\omega t )\)
Daher kann \( v_i \) auch als
\( v_i \) ist gleich dem Realteil von \( e^{j \omega t} \)
Wir lassen nun den "Realteil von" weg und führen alle Berechnungen in komplexen Zahlen durch und definieren \( V_i \) in komplexer Form als
\( V_i = V_0 e^{j \omega t} \)
und leiten \( I \) in komplexer Form ab:
\( I = \frac{V_0 e^{j\omega t}}{|Z| \; \angle \; \theta} \)
und \( I \) in Polardarstellung lautet:
\( I = \dfrac{V_0}{|Z|} \; \angle \; \omega t - \theta \)
\( I = I_0 \; \angle \; \omega t - \theta \), wobei \( I_0 = \dfrac{V_0}{|Z|} \)
Schreiben Sie die Impedanzen \( Z_R, Z_L\) und \( Z_C \) in Polardarstellung um:
\( Z_R = R = R \; \angle \; 0 \)
\( Z_L = j \omega L = \omega L \; \angle \; \pi/2\)
\( Z_C = - \dfrac{1}{\omega C} j = \dfrac{1}{\omega C} \; \angle \; - \pi/2\ \)
Die Spannungen sind gegeben durch
\( V_R = Z_R I = (R \; \angle \; 0) (I_0 \; \angle \; {\omega t - \theta}) = R I_0 \angle \; \omega t - \theta \)
\( V_L = Z_L I = (\omega L \; \angle \; \pi/2) (I_0 \; \angle \; {j\omega t - \theta}) = \omega L I_0 \; \angle \; {\omega t - \theta + \pi/2} \)
\( V_C = Z_C I = (\dfrac{1}{\omega C} \; \angle \; - \pi/2) (I_0 \; \angle \; {j\omega t - \theta}) = \dfrac{I_0}{\omega C} \; \angle \; {\omega t - \theta - \pi/2} \)
Der Strom \( I \) und die Spannungen \( V_R \), \( V_C \) und \( V_C \) werden unten mit Phasoren dargestellt.

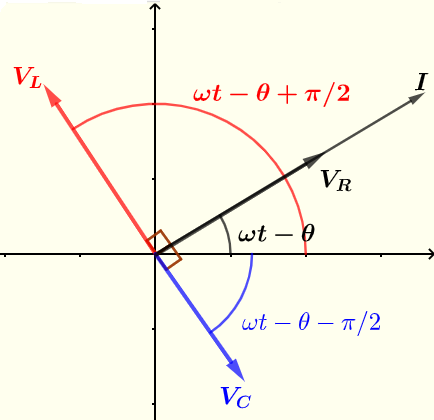
Der reale Strom und die realen Spannungen werden durch den Realteil der komplexen (oder polar) Form des oben erhaltenen Stroms und der Spannungen gegeben.
\( i = \dfrac{V_0}{|Z|} \cos( \omega t - \theta) \)

\( v_R = R \dfrac{V_0}{|Z|} \cos(\omega t - \theta) \)

\( v_L = \omega L \dfrac{V_0}{|Z|} \cos(\omega t - \theta + \pi/2) \)

\( v_C = \dfrac{V_0}{\omega C|Z|} \cos(\omega t - \theta - \pi/2) \)

HINWEIS: Die Zeitabhängigkeit \( \omega t \) kann während der Berechnungen weggelassen werden und am Ende hinzugefügt werden, wenn wir Strom und Spannungen als Funktion der Zeit schreiben müssen. Die untenstehenden Beispiele zeigen, wie RLC-Schaltkreise unter Ignorierung der Zeitabhängigkeit analysiert werden.

C - Beispiele mit Detaillierten Lösungen

Beispiel 1
In einem Serien-RLC-Schaltkreis ist die Quellspannung gegeben durch \( v_i = 20 \cos (\omega t) \), wobei \( \omega = 1000 \; rad/s \), die Kapazität des Kondensators \( C = 200 \; \mu F \), die Induktivität der Spule \( L = 400 \; mH\) und der Widerstand des Widerstands \( R = 400 \; \Omega \).
a) Bestimmen Sie die Impedanzen des Kondensators, der Induktivität und des Widerstands sowie die Impedanz \( Z \), die dem RLC-Schaltkreis in komplexer Form entspricht.
b) Bestimmen Sie den Strom und alle Spannungen in komplexer Form.
c) Bestimmen Sie den realen Strom und die realen Spannungen.

Lösung zu Beispiel 1
a)
Die Impedanz in komplexer Form \( Z_R \) eines Widerstands mit dem Widerstand \( R \) ist gegeben durch
\( Z_R = R = 400 \; \Omega \)
Die Impedanz in komplexer Form \( Z_L \) einer Induktivität mit der Induktivität \( L \), auch als induktiver Blindwiderstand bezeichnet, ist gegeben durch
\( Z_L = j \omega L = j \cdot 1000 \cdot 400 \cdot 10^{-3} = 400 j \; \Omega \)
Die Impedanz in komplexer Form \( Z_C \) eines Kondensators mit der Kapazität \( C \), auch als kapazitiver Blindwiderstand bezeichnet, ist gegeben durch
\( Z_C = - \dfrac{1}{\omega C} j = - \dfrac{1}{1000 \cdot 200 \cdot 10^-6} j = - 5 j \; \Omega \)
\( Z = Z_R + Z_L + Z_C = 400 + 400 j - 5 j = 400 + 395 j \)
b)
\( v_i = 20 \cos (\omega t) \), daher ist die Polardarstellung der Quellspannung \( V_i = 20 \; \angle \; 0\)
Wir haben oben gesehen, dass der Strom in Polardarstellung gegeben ist durch
\( I = \dfrac{V_i}{Z_R + Z_L + Z_C } \)
Setzen Sie die bekannten Größen ein:
\( I = \dfrac{20 \; \angle \; 0}{400 + 395 j}\)
Schreiben Sie den Nenner in Polardarstellung um:
\( 400 + 395 j = \sqrt {400^2+395^2} \; \angle \; \arctan\left(\dfrac{395}{400}\right) = 562,16 \; \angle \; 44,64^{\circ} \)
Berechnen Sie \( I \)
\( I = \dfrac{20 \; \angle \; 0}{562,16 \; \angle \; 44,64^{\circ}} = \dfrac{20}{562,16} \; \angle \; 0 - 44,64^{\circ} \)
Vereinfachen:
\( I = 0,0356 \; \; \angle \; - 44,64^{\circ} \) A
\( V_R = R I = 400 (0,0356 \; \; \angle \; - 44,64^{\circ}) = 14,24 \; V \; \angle \; - 44,64^{\circ}\) V
\( V_L = Z_L I = 400 j (0,0356 \; \; \angle \; - 44,64^{\circ}) = 14,24 \; V \; \angle \; 45,36^{\circ}\) V
\( V_C = Z_C I = - 5 j (0,0356 \; \; \angle \; - 44,64^{\circ}) = 0,18 \; V \; \angle \; -134,6^{\circ}\) V

Beispiel 2
In einem Serien-RLC-Schaltkreis ist die Quellspannung gegeben durch \( v_i = 10 \cos (\omega t) \), die Kapazität des Kondensators \( C = 200 \; \mu F \), die Induktivität der Spule \( L = 200 \; mH\) und der Widerstand des Widerstands \( R = 500 \; \Omega \).
a) Bestimmen Sie die Winkelgeschwindigkeit \( \omega \), bei der der Imaginärteil der Impedanz \( Z \) gleich null ist.
b) Bestimmen Sie den Strom und die Spannungen für die in Teil a) gefundene Frequenz.

Lösung zu Beispiel 2
a)
Für einen Serien-RLC-Schaltkreis \( Z = R + j(\omega L - \dfrac{1}{\omega C} ) \)
Der Imaginärteil von \( Z \) ist gleich null ergibt
\( \omega L - \dfrac{1}{\omega C} = 0 \)
Lösen Sie für \( \omega \)
\( \omega^2 L C = 1 \)
\( \omega = \dfrac{1}{\sqrt{L C}} \)
Setzen Sie \( L \) und \( C \) durch ihre numerischen Werte ein
\( \omega = \dfrac{1}{ \sqrt{ 200\cdot10^{-3} \cdot 200 \cdot 10^{-6}}} = 158,11 \) rad/s
b)
\( I = \dfrac{V_i}{Z} = \dfrac{10 \; \angle \; 0}{R \; \angle \; 0} = \dfrac{10}{500} \; \angle \; 0 = 0,02 \; \angle\; 0 \)
\( V_R = R I = 500 \cdot 0,02 \; \angle \; 0 = 10 \; \angle\; 0 \)
\( V_C = Z_C I = \dfrac{1}{\omega C} \; \angle \; -90^{\circ} \cdot 0,02 \; \angle\; 0 = \dfrac{1}{\omega C} \cdot 0,02 \; \angle \; -90^{\circ} = \dfrac{1}{158,11 \cdot 200 \cdot 10^{-6}} \cdot 0,02 \; \angle \; -90^{\circ} = 0,6324 \; \angle \; -90^{\circ} \)
\( V_L = Z_L I = \omega L \; \angle \; 90^{\circ} \cdot 0,02 \; \angle\; 0 = \omega L \cdot 0,02 \; \angle \; 90^{\circ} = 158,11 \cdot 200 \cdot 10^{-3} \cdot 0,02 \; \angle \; 90^{\circ} = 0,6324 \; \angle \; 90^{\circ} \)

Beispiel 3
In einem Serien-RLC-Schaltkreis ist die Quellspannung gegeben durch \( v_i = V_0 \cos (2 \pi f t) \), wobei \( f \) die Frequenz ist, die Kapazität des Kondensators \( C = 47 \; \mu F \), die Induktivität der Spule \( L = 100 \; mH\) und der Widerstand des Widerstands \( R = 200 \; \Omega \).
a) Bestimmen Sie die Gesamtimpedanz \( Z \), die dem Kondensator, der Induktivität und dem Widerstand in Serie entspricht, in Abhängigkeit von der Frequenz \( f \), und schreiben Sie sie in Polardarstellung \( Z = |Z| \; \angle \; \theta \)
b) Bestimmen Sie die Frequenz \( f \), sodass \( \theta = -60^{\circ} \) ist.

Lösung zu Beispiel 3
a)
Für einen Serien-RLC-Schaltkreis \( Z = R + j(\omega L - \dfrac{1}{\omega C}) \)
Setzen Sie die bekannten Größen durch ihre numerischen Werte ein
\( Z = R + j(\omega L - \dfrac{1}{\omega C}) = 200 + j( \omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}})\)
\( Z = \sqrt {200^2 + ( \omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}})^2} \; \angle \; \arctan \left(\dfrac{\omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}}}{200}\right) \)
b)
\( \arctan \left(\dfrac{\omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}}}{200}\right) = -60^{\circ} \)
\( \dfrac{\omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}}}{200} = \tan (-60^{\circ}) = -1,73205 \)
Multiplizieren Sie alle Terme der Gleichung mit \( 200 \), um den Nenner zu eliminieren
\( \omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}} = -346,41 \)
Multiplizieren Sie alle Terme der Gleichung mit \( \omega \cdot 47 \cdot 10^{-6} \), um den Nenner zu eliminieren
\( 47 \cdot 10^{-7} \omega^2 - 1 = -0,01628127 \omega \)
Lösen Sie die obige quadratische Gleichung nach \( \omega \) und wählen Sie die positive Lösung.
\( \omega = 53,23 \) rad/s
\( \omega = 2 \pi f = 60,3682 \)
\( f = \dfrac{60,3682}{2 \pi} = 9,60789 \) Hz

Beispiel 4
In einem Serien-RLC-Schaltkreis ist die Quellspannung gegeben durch \( v_i = V_0 \cos (2 \pi f t) \), die Kapazität des Kondensators \( C = 470 \mu \)F, die Induktivität der Spule \( L = 50 \)mH und der Widerstand des Widerstands ist \( R \).
a) Bestimmen Sie die Gesamtimpedanz \( Z \), die dem Kondensator, der Induktivität und dem Widerstand in Serie entspricht, in Abhängigkeit von der Frequenz \( f \), und schreiben Sie sie in Polardarstellung \( Z = |Z| \; \angle \; \theta \)
b) Bestimmen Sie den Widerstand \( R \) und die Frequenz \( f \), sodass \( \theta = 40^{\circ} \) und \( |Z| = 100 \) sind.

Lösung zu Beispiel 4
a)
Für einen Serien-RLC-Schaltkreis \( Z = R + j(\omega L - \dfrac{1}{\omega C}) \)
Schreiben Sie \( Z \) in Polardarstellung
\( Z = \sqrt{R^2 + (\omega L - \dfrac{1}{\omega C})^2} \; \angle \; \arctan \left( \dfrac{\omega L - \dfrac{1}{\omega C}}{R} \right) \)
b)
\( \theta = \arctan \left( \dfrac{\omega L - \dfrac{1}{\omega C}}{R} \right) = 40^{\circ} \)
\( \dfrac{\omega L - \dfrac{1}{\omega C}}{R} = \tan 40^{\circ} = 0,83909\)
\( \omega L - \dfrac{1}{\omega C} = 0,83909 R \)
Setzen Sie das Obige in \( |Z| \) ein
\( \sqrt{R^2 + (0,83909 R)^2} = 100 \)
Lösen Sie für \( R \)
\( R = 76,6048 \; \Omega \)
\( \omega L - \dfrac{1}{\omega C} = 0,83909 R = 64,27832 \)
Lösen Sie für \( \omega \)
\( \omega = 1317,8557 \) rad/s
\( f = \dfrac{1317,8557}{2\pi} = 209,74324 \) Hz

Weitere Referenzen und Links