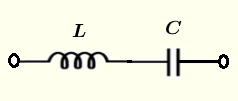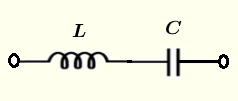Rechner für Serien-LC-Schaltungsimpedanz
Inhaltsverzeichnis
Ein Rechner zur Berechnung der äquivalenten Impedanz eines Induktors und eines Kondensators in Serie.
Komplexe Zahlen in Standardform und
Polarform werden in den Berechnungen und bei der Darstellung der Ergebnisse verwendet.
\( \) \( \) \( \)
Formeln für die Impedanz der Serien-LC-Schaltung, die im Rechner verwendet werden, und deren Einheiten
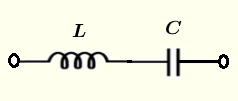
Sei \( f \) die Frequenz, in Hertz, der Versorgungsspannung der Schaltung.
Definieren Sie die folgenden Parameter, die in den Berechnungen verwendet werden
\( \omega = 2 \pi f \) , Winkelgeschwindigkeit in rad/s
\( X_L = \omega L \) , die induktive Reaktanz in Ohm \( (\Omega) \)
Die Impedanz des Induktors \( L \) wird durch
\( Z_L = j \omega L \)
\( X_C = 1 / (\omega C) \) , die kapazitive Reaktanz in Ohm \( (\Omega) \)
Die Impedanz des Kondensators \( C \) wird durch
\( Z_C = \dfrac{1}{j \omega C} = -\dfrac{j}{\omega C}\)
Sei \( Z \) die äquivalente Impedanz der oben gezeigten Serien-LC-Schaltung und schreibe sie in komplexer Form wie folgt
\[ Z = Z_L + Z_C = j\omega L - \dfrac{j}{\omega C} = j \left(\omega L - \dfrac{1}{\omega C} \right) \]
Die Formeln für den Betrag \( |Z| \) und das Argument (oder den Phasenwinkel) \( \theta \) von \( Z \) lauten wie folgt
Betrag: \( |Z| = \left| \omega L - \dfrac{1}{\omega C} \right| \)
Argument (Phase): \( \theta = \dfrac{\pi}{2} \) oder \( 90^{\circ} \) wenn \( \omega L \gt \dfrac{1}{\omega C} \)
Argument (Phase): \( \theta = - \dfrac{\pi}{2} \) oder \( - 90^{\circ} \) wenn \( \omega L \lt \dfrac{1}{\omega C} \)
Argument (Phase): \( \theta = 0 \) wenn \( \omega L = \dfrac{1}{\omega C} \)
Verwendung des Rechners
Geben Sie den Widerstand, die Kapazität und die Frequenz als positive reelle Zahlen mit den angegebenen Einheiten ein und drücken Sie dann "Berechnen".
Ergebnisse der Berechnungen
Weitere Referenzen und Links
Wechselstrom-Schaltungsrechner und -Löser
Komplexe Zahlen - Grundoperationen
Komplexe Zahlen in Exponentialform
Komplexe Zahlen in Polarform
Umwandlung einer komplexen Zahl in Polar- und Exponentialform-Rechner
Ingenieurmathematik mit Beispielen und Lösungen