La définition des fonctions à plusieurs variables et le concept de domaine de ces fonctions sont présentés avec des exemples.
Problèmes et leurs solutions sont également inclus.
Des compétences en résolution de systèmes d'inégalités à deux variables sont nécessaires pour trouver le domaine des fonctions à deux variables.
Considérons quelques formules très connues.
a) Le périmètre \( P \) d'un carré de côté \( x \) est donné par \( P = 4 x\).
b) L'aire \( A \) d'un rectangle de longueur \( L \) et de largeur \( W \) est donnée par \( A = L W \)
c) La force \( F \), selon la loi universelle de la gravitation de Newton, entre deux objets de masses \( m_1 \) et \( m_2 \) séparés par une distance \( d \) est donnée par \( F = G \dfrac{m_1 m_2}{d^2} \)
où \( G \) est une constante.
On peut dire que :
le périmètre \( P \) dans la partie a) ci-dessus est une fonction d'une variable \( x \)
l'aire \( A \) dans la partie b) ci-dessus est une fonction de deux variables \( L \) et \( W \)
la force \( F \) dans la partie c) est une fonction de trois variables \( m_1 \), \( m_2 \) et \( d \) (Note que G est une constante).
Une fonction \( f \) de \( n \) variables \( x_1, x_2, ...., x_n \), est une règle qui associe un nombre réel unique \( f (x_1, x_2, ...., x_n) \) à chaque n-uplet de nombres réels \( x_1, x_2, ...., x_n \).
L'ensemble \( D \) de tous les n-uplets de nombres réels \( x_1, x_2, ...., x_n \) pour lesquels la fonction \( f \) est une valeur réelle unique est appelé le domaine de la fonction \( f \).
Si nous laissons \( u = f (x_1, x_2, ...., x_n) \), l'ensemble de toutes les valeurs de \( u \) correspondant à tous les n-uplets \( x_1, x_2, ...., x_n \) dans \( D \) est appelé l'ensemble des images de \( f \) [1] , [2] , [3] .
Exemple 1 Fonction de deux Variables
Soit la fonction \( f \) définie par
\[ f(x,y) = \sqrt{x^2+y^2} + \ln(x-y) \]
a) Évaluer : \( f(4,3) \) , \( f(e^2,0) \)
b) Trouver et esquisser le domaine de \( f \)
Solution de l'Exemple 1
a)
Pour évaluer \( f(4,3) \), nous devons remplacer \( x \) par \( 4 \) et \( y \) par \( 3 \)
Ainsi
\( f(4,3) = \sqrt{4^2+3^2} + \ln(4-3) \)
Simplifier
\( \quad = \sqrt{25} + \ln(1) = 5 + 0 = 5 \)
Pour évaluer \( f(e^2,0) \), nous devons remplacer \( x \) par \( e^2 \) et \( y \) par \( 0 \)
Ainsi
\( f(e^2,0) = \sqrt{e^2 + 0^2} + \ln(e^2 - 0) \)
Simplifier
\( \quad = e + 2 \)
b)
Le domaine de \( f(x,y) \) est trouvé en fixant les conditions :
1) \( \quad x^2+y^2 \ge 0 \), une quantité sous la racine carrée doit être non négative
2) \( \quad x - y \gt 0 \), l'argument d'un logarithme doit être positif.
La condition 1) ci-dessus est toujours satisfaite.
L'inégalité de la condition 2) peut être résolue graphiquement pour obtenir la solution montrée par le graphique ci-dessous.

Exemple 2 Fonction de trois Variables
Soit la fonction \( g \) définie par
\[ g(x,y,z) = \sqrt{ x^2 + y^2 + z^2 - 9} \]
a) Évaluer : \( g(3,-1,1) \) , \( g(3/2,1/4,7/2) \)
b) Trouver et décrire le domaine de \( g \)
Solution de l'Exemple 2
a)
Pour évaluer \( g(3,-1,1) \) , nous devons remplacer \( x \) par \( 3 \), \( y \) par \( -1 \) et \( z \) par \( 1 \)
Ainsi
\( g(3,-1,1) = \sqrt{ 3^2 + (-1)^2 + 1^2 - 9} \)
Simplifier
\( \quad = \sqrt{2} \)
Pour évaluer \( g(3/2,1/4,7/2) \), nous devons remplacer \( x \) par \( 3/2 \), \( y \) par \( 1/4 \) et \( z \) par \( 7/2 \)
Ainsi
\( g(3/2,1/4,2) = \sqrt{ (3/2)^2 + (1/4)^2 + (7/2)^2 - 9} \)
Simplifier
\( \quad = \dfrac{\sqrt{89}}{4} \)
b)
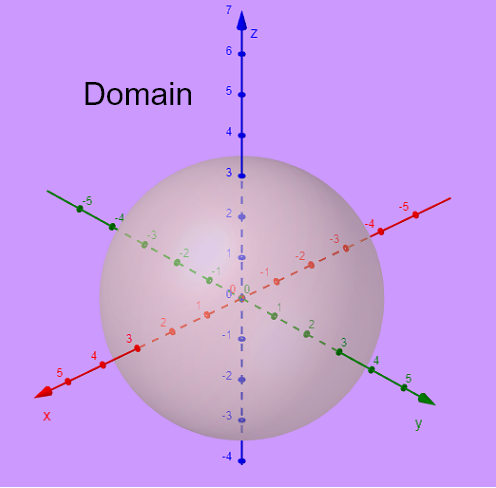
Le domaine de \( g(x,y,z) \) est trouvé en fixant les conditions :
\( x^2 + y^2 + z^2 - 9 \ge 0 \) , une quantité sous la racine carrée doit être non négative
Considérons \( x^2 + y^2 + z^2 - 9 = 0 \) qui peut être écrit comme \( x^2 + y^2 + z^2 = 3^2 \).
Ainsi, le graphe de l'équation \( x^2 + y^2 + z^2 - 9 = 0 \) est une sphère de rayon \( 3 \) centrée à l'origine \( (0,0,0) \) comme montré ci-dessous.
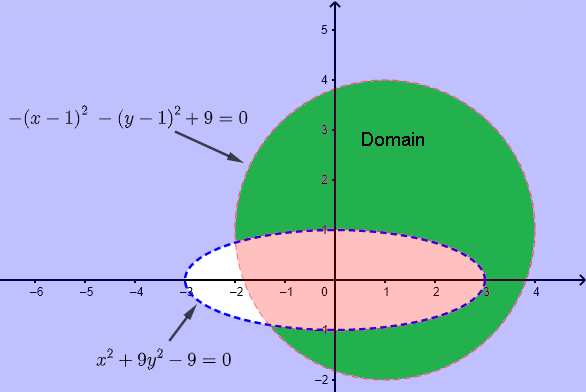
Exemple 3 Fonction de deux Variables
Soit la fonction \( h \) définie par
\[ h(x,y) = \dfrac{1}{\ln (1 - x y) } - \sqrt{x - y^2}\]
a) Trouver et décrire le domaine de \( h \)
b) Donner des exemples de 3 paires ordonnées \( (x,y) \) qui sont dans le domaine de \( h \) et évaluer la fonction en ces points.
c) Donner des exemples de 3 paires ordonnées \( (x,y) \) qui NE sont PAS dans le domaine.
Solution de l'Exemple 3
a)
Le domaine de \( h(x,y) \) est trouvé en fixant les conditions :
1) \( \quad 1 - x y \gt 0 \) , l'argument d'un logarithme doit être positif
2) \( \quad x - y^2 \ge 0 \) , l'argument de la racine carrée doit être non négatif.
3) \( \quad \ln (1 - x y) \ne 0 \) ou \( 1 - xy \ne 1 \) ce qui est équivalent à \( xy \ne 0 \), le dénominateur \( \ln (1 - x y) \) ne doit PAS être égal à zéro.
La condition 1) est résolue en traçant \( 1 - x y = 0 \) ce qui est équivalent à \( y = \dfrac{1}{x} \) et en sélectionnant l'ensemble des solutions comme étant l'ensemble des points satisfaisant l'inégalité \( \quad 1 - x y \gt 0 \). (couleur violet clair)
La condition 2) est résolue en traçant \( x - y^2 = 0 \) ce qui est équivalent à \( x = y^2 \), une parabole horizontale, et en sélectionnant l'ensemble des solutions comme étant l'ensemble des points satisfaisant l'inégalité \( \quad x - y^2 \ge 0 \). (couleur rouge)
La condition 3) est satisfaite par tous les points qui ne sont pas sur l'un des axes. (lignes brisées sur les axes)
Le domaine est l'intersection de tous les trois ensembles trouvés pour les conditions 1), 2) et 3) et est montré ci-dessous en vert excluant tout point sur les axes \( x \) ou \( y \).
Partie A
Étant donné les fonctions :
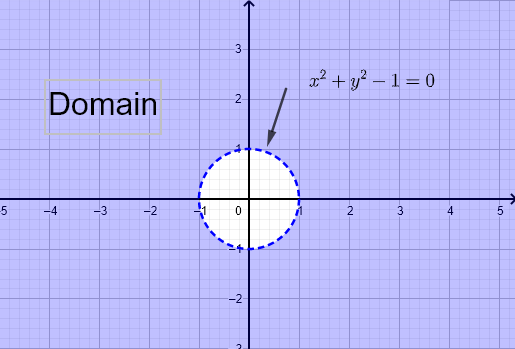
\( f (x,y) = \dfrac{1}{\sqrt{x^2 - y}} \) et \( g (x,y) = \ln (x^2 + y^2 - 1) \)
a) Trouver le domaine de chaque fonction
b) Évaluer
1) \( f (1,0) \) , 2) \( g (1,-1) \) , 3) \( \dfrac{f(3,4)}{g(2,0)} \)
Partie B
Dans un circuit électrique, la résistance \( R \) de trois résistances en parallèle et de résistances \( r_1 , r_2 , r_3 \) sont reliées par
\( \dfrac{1}{R} = \dfrac{1}{r_1} + \dfrac{1}{r_2} + \dfrac{1}{r_3} \)
a) Exprimer \( R \) comme une fonction des variables \( r_1 , r_2 , r_3 \).
b) Calculer \( R \) pour \( r_1 = 100 \) , \( r_2 = 50 \) et \( r_3 = 20 \).
Partie C
Trouver le domaine des fonctions
a) \( f(x,y) = \sqrt{x^2+y-2x} \)
b) \( h(x,y) = \dfrac{\ln(x^2+9 y^2-9)}{\sqrt{7-x^2-y^2+2 x + 2 y}} \)
Partie A
\( f (x,y) = \dfrac{1}{\sqrt{x^2 - y}} \) et \( g (x,y) = \ln (x^2 + y^2 - 1) \)
a)
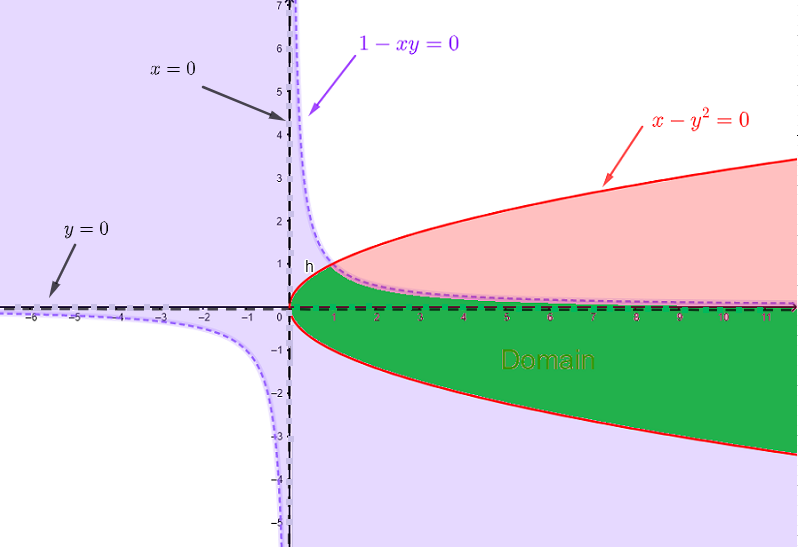
Le domaine de \( f \) est trouvé en résolvant : \( x^2 - y \gt 0 \); le dénominateur ne doit pas être égal à zéro et l'argument de la racine carrée doit être non négatif.
Tracer \( y = x^2 \) et sélectionner la zone satisfaisant l'inégalité \( x^2 - y \gt 0 \). La solution graphique est montrée ci-dessous. Le domaine est l'ensemble de tous les points \( (x,y) \) à l'extérieur de la parabole \( y = x^2 \).

Partie B
a)
Étant donné \( \dfrac{1}{R} = \dfrac{1}{r_1} + \dfrac{1}{r_2} + \dfrac{1}{r_3} \),
Multipliez tous les termes de l'équation par le produit \( r_1 r_2 r_3 \)
\( \dfrac{r_1 r_2 r_3}{R} = \dfrac{r_1 r_2 r_3}{r_1} + \dfrac{r_1 r_2 r_3}{r_2} + \dfrac{r_1 r_2 r_3}{r_3} \)
Simplifiez
\( \dfrac{r_1 r_2 r_3}{R} = r_2 r_3 + r_1 r_3 + r_1 r_2 \)
Résoudre pour \( R \)
\( R(r_1,r_2,r_3) = \dfrac{r_1 r_2 r_3}{r_2 r_3 + r_1 r_3 + r_1 r_2} \)
b)
\( R(100,50,20) = \dfrac{100 \times 50 \times 20}{50 \times 20 + 100 \times 20 + 100 \times 50} = 12.5\)
Partie C
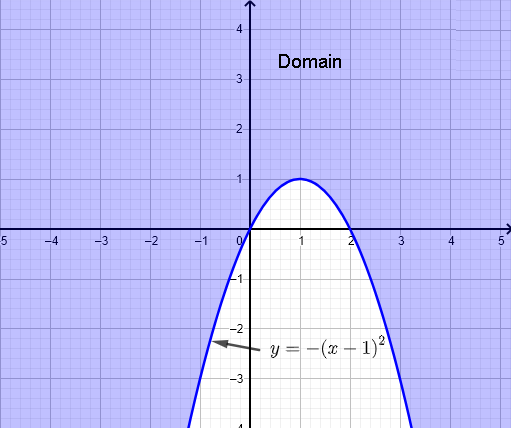
a) \( f(x,y) = \sqrt{x^2+y-2x} \)
\( f(x,y) \) prend des valeurs réelles si l'argument de la racine carrée est non négatif, d'où la condition
\( x^2+y-2x \ge 0 \)
Complétez le carré et réécrivez comme
\( (x-1)^2 - 1 + y \ge 0 \)
\( y \ge - (x-1)^2 + 1 \)
Tracez la parabole \( y = - (x-1)^2 + 1 \) et identifiez le domaine de la fonction \( f \).
Le domaine est l'ensemble des points \( (x,y) \) sur ou à l'extérieur de la parabole \( y = - (x-1)^2 + 1 \) comme montré dans le graphique ci-dessous (violet).