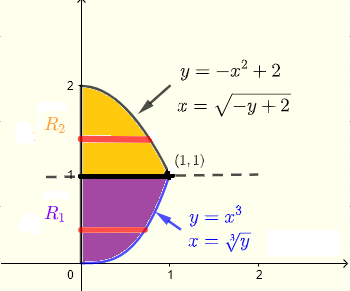Table of Contents
Intégrales Doubles sur des Régions Générales
Des exemples pour calculer et évaluer les intégrales doubles sur des régions générales
sont présentés avec leurs solutions détaillées.
Notes Importantes
1) Faire des graphiques et des diagrammes pour des régions générales non rectangulaires en première étape facilite le calcul des intégrales doubles sur des régions générales.
2) En général, quatre étapes sont nécessaires pour calculer une intégrale double sur des régions générales d'intégration :
ÉTAPE 1 : Faire un graphique et/ou un diagramme de la région d'intégration
ÉTAPE 2 : Décider comment décrire la région générale en utilisant soit des bandes verticales soit des bandes horizontales et donc l'ordre d'intégration
ÉTAPE 3 : Décrire la région générale d'intégration en utilisant des inégalités
ÉTAPE 4 : Calculer l'intégrale
3) Dans ce qui suit, nous décrivons une région donnée \( R \) d'intégration soit comme un ensemble infini de bandes verticales ce qui permet à l'intégrale d'être exprimée
comme \( \displaystyle \iint_R f(x,y) \;dy \;dx \) ou des bandes horizontales ce qui permet à l'intégrale d'être exprimée comme \( \displaystyle \iint_R f(x,y) \;dx \;dy \)
\( \)\( \)\( \)
Calculs des Intégrales Doubles sur des Régions Générales
Les objectifs des exemples 1 et 2 consistent à utiliser des graphiques et des diagrammes pour déterminer les limites d'intégration pour des régions générales et calculer l'intégrale double.
Exemple 1
Question : Calculer l'intégrale double \( \displaystyle V = \iint_R (x^2+y) \;dy \;dx \) où la région \( R \) est un triangle sur le plan \( xy\)-plane délimité par l'axe des \(x\), l'axe des \(y\) et la droite \( y = - x + 2 \).
Solution de l'Exemple 1
Quatre étapes majeures pour calculer les intégrales doubles sur des régions générales d'intégration.
ÉTAPE 1 Faire un graphique et/ou un diagramme représentant la région générale
Nous commençons d'abord par dessiner un graphique ou/et un diagramme de la région \( R \) d'intégration. Dans cet exemple, il s'agit d'un triangle avec des côtés sur l'axe des \(x\) et l'axe des \(y\), et le troisième côté est décrit par l'équation de la droite \( y = - x + 2 \).
Ce triangle peut également être défini par trois sommets : l'origine et les points d'intersection de la droite \( y = - x + 2 \) avec les axes des \(x\) et des \(y\) donnés par \( (2,0) \) et \( (0,2) \) respectivement, comme indiqué dans le graphique ci-dessous.

Il existe deux façons de calculer l'intégrale donnée sur la région donnée.
ÉTAPE 2 Décider comment décrire la région générale en utilisant des bandes
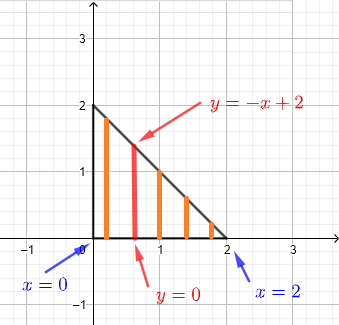
1) Nous utilisons des bandes verticales pour décrire la région \( R \) comme indiqué dans le graphique ci-dessous.
Nous supposons que la région \( R \) peut être considérée comme un ensemble infini de bandes verticales comme indiqué dans le diagramme ci-dessous.
Toute bande verticale donnée, pour une valeur donnée de \( x \), commence à \( y = 0 \) et se termine à \( y = - x + 2 \). Puisque nous devons inclure toutes les bandes qui décrivent la région \( R \), \( x \) doit prendre des valeurs de \( x = 0 \) à \( x = 2 \). Par conséquent, la région \( R \) d'intégration peut être définie par :
ÉTAPE 3 Décrire la région générale d'intégration en utilisant des inégalités
\( R \) : \( 0 \le x \le \ 2 \) , \( 0 \le y \le - x + 2 \)
ÉTAPE 4 Calculer l'intégrale
L'intégrale peut être écrite comme
\( \displaystyle V = \int_0^2 \int_0^{-x+2} (x^2+y) \;dy \;dx \)
\( = \displaystyle \int_0^2 ( -x^3 +\dfrac{5}{2} x^2 - 2x + 2) \;dx = 8/3\)
Nous répondons maintenant à la même question mais en utilisant des bandes horizontales.
ÉTAPE 1 est la même que ci-dessus
ÉTAPE 2 Décider comment décrire la région générale en utilisant des bandes
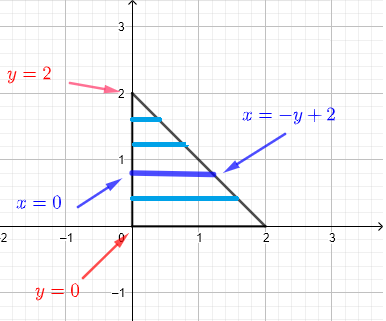
2) Nous utilisons des bandes horizontales pour décrire la région \( R \) comme indiqué dans le graphique ci-dessous.
Nous supposons que la région \( R \) peut être considérée comme un ensemble infini de bandes horizontales comme indiqué dans le diagramme ci-dessous.
Toute bande verticale donnée, pour une valeur donnée de \( y \), commence à \( x = 0 \) et se termine à \( x = - y + 2 \). Puisque nous devons inclure toutes les bandes qui décrivent la région \( R \), \( y \) doit prendre des valeurs de \( y = 0 \) à \( y = 2 \). Par conséquent, la région \( R \) d'intégration peut être définie par :
ÉTAPE 3 Décrire la région générale d'intégration en utilisant des inégalités
\( R \) : \( 0 \le x \le - y + 2 \) , \( 0 \le y \le 2 \)
ÉTAPE 4 Calculer l'intégrale
Par conséquent, l'intégrale peut être écrite comme
\( \displaystyle V = \int_0^2 \int_0^{-y+2} (x^2+y) \;dx \;dy \)
\( = \displaystyle \int_0^2 (-\dfrac{1}{3} y^3 + y^2 - 2 y + \dfrac{8}{3} ) \;dy = 8/3 \)
Remarques Dans les deux cas, l'intégrale dont les limites incluent des variables est l'intégrale intérieure
Example 2
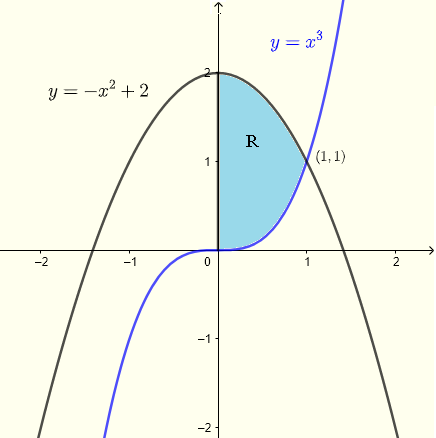
Question: Calculez l'intégrale double \( \displaystyle V = \iint_R (x+y) \;dy \;dx \) où la région \( R \) est dans le plan \( xy\)-plane bornée par l'axe des \(y\), les courbes d'équations \( y = x^3 \) et \( y = - x^2 + 2 \).
Solution de l'exemple 2
Nous commençons par analyser la région \( R \) comme indiqué dans le graphique ci-dessous. Les deux courbes se croisent en un point dont la coordonnée \( x \) est donnée par la solution du système d'équations
\( y = x^3 \)
\(y = - x^2 + 2 \)
Une façon de résoudre le système ci-dessus est de soustraire les deux équations et de simplifier pour éliminer \( y \) et obtenir une équation en \(x \) seulement pour obtenir l'équation
\( 0 = x^3 + x^2 - 2 \)
Avec l'aide du graphique, il est facile de voir que \( x = 1 \) est une solution du système d'équation ci-dessus que vous pouvez vérifier analytiquement.
La coordonnée \(y\) du point d'intersection des deux courbes est trouvée en substituant \( x \) par la solution déjà trouvée \( 1 \) dans l'une des équations des courbes pour trouver \( y = (1)^3 = 1 \).
Ainsi, le point d'intersection est donné par \( (1,1) \)
1) En utilisant des bandes verticales
Une bande verticale donnée commence sur la courbe \( y = x^3 \) et se termine sur la courbe \( x = - x^2 + 2 \). Pour toute la région, \( x \) doit prendre toutes les valeurs de \( x = 0 \) à \( x = 1 \). Ainsi, la région \( R \) d'intégration est donnée par
\( R \) : \( 0 \le x \le 1 \) , \( x^3 \le y \le - x^2 + 2 \)
Ainsi, l'intégrale peut être calculée comme suit
\( \displaystyle V = \int_0^1 \int_{x^3}^{-x^2+2} (x+y) \;dy \;dx = \dfrac{803}{420}\)
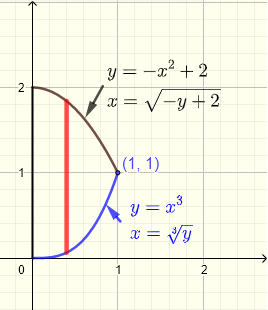
2) En utilisant des bandes horizontales
Une bande horizontale donnée commence sur l'axe \(y\) \( x = 0 \) et se termine soit sur la courbe \( x = \sqrt[3]y \) soit sur la courbe \( x = \sqrt{- y+ 2} \). En raison des deux courbes différentes, la région \( R \) peut être divisée en deux régions \( R_1 \) et \( R_2 \).
Pour la région \( R_1 \), \( y \) doit prendre toutes les valeurs de \( y = 0 \) à \( y = 1 \) et pour la région \( R_2 \), \( y \) doit prendre toutes les valeurs de \( y = 1 \) à \( y = 2 \).
Ainsi, la région \( R \) d'intégration a deux parties :
\( R_1 \) : \( 0 \le x \le \sqrt[3]y \) , \( 0 \le y \le 1 \)
et
\( R_2 \) : \( 0 \le x \le \sqrt{- y+
2} \) , \( 0 \le y \le 1 \)
Ainsi, l'intégrale peut être calculée comme suit
\( \displaystyle V = \iint_{R_1} (x+y) \;dx \;dy + \iint_{R_2} (x+y) \;dx \;dy \)
\( \displaystyle = \int_0^1 \int_{0}^{\sqrt[3]y} (x+y) \;dx \;dy + \int_1^2 \int_{0}^{\sqrt{-y+2}} (x+y) \;dx \;dy = \dfrac{803}{420}\)
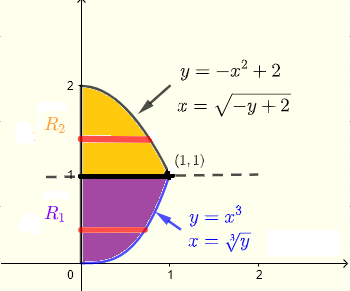
Exemples où le choix de l'ordre d'intégration dépend du problème donné
Dans les exemples 3, 4 et 5, nous montrons parfois que nous n'avons pas les deux choix de l'ordre d'intégration que nous avons habituellement dans les intégrales doubles.
Les objectifs des exemples 3, 4 et 5 consistent à utiliser des graphiques et des diagrammes pour déterminer l'ordre d'intégration qui mène au calcul analytique de l'intégrale double.
Exemple 3
Question: Évaluez l'intégrale double \( \displaystyle V = \int _0^1 \int _y^1 (y + e^{-x^2}) dx dy \) si possible. Inversez l'ordre d'intégration si nécessaire pour évaluer l'intégrale donnée.
Solution de l'exemple 3
Commençons par l'intégrale interne
Soit
\( \displaystyle I = \int _y^1 (y+e^{-x^2}) dx \)
En essayant d'évaluer \( I \) ci-dessus, l'intégrale \( \displaystyle I = \int _y^1 (e^{-x^2}) dx \) ne peut pas être effectuée analytiquement.
Selon les limites d'intégration données, la région \( R \) d'intégration de l'intégrale \( V \) peut être écrite comme
\( R \) : \( y \le x \le 1 \) , \( 0 \le y \le 1 \)
avec le graphique ci-dessous comme un ensemble de bandes horizontales.
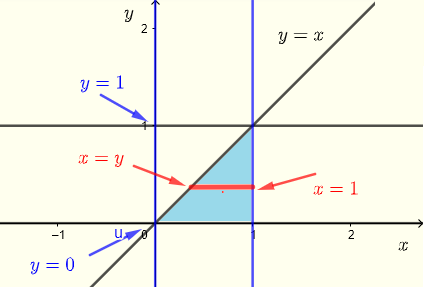
Utilisons maintenant des bandes verticales pour décrire la région \( R \) comme indiqué dans le graphique ci-dessous.
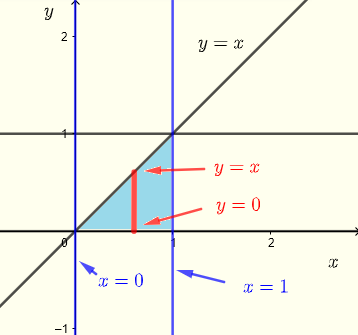
\
Tracer la région \( R \) d'intégration pour voir si en changeant l'ordre d'intégration, nous pouvons aller plus loin.
\( R \) : \( 0 \le x \le 1 \) , \( 0 \le y \le x \)
L'intégrale \( V \) peut être écrite comme
\( \displaystyle V = \int _0^1 \int _0^x (y + e^{-x^2}) dy dx \)
Évaluons en utilisant l'intégrale interne \( I \) donnée par
\( \displaystyle I = \int _0^x (y + e^{-x^2}) dy \)
\( = \left[ \dfrac{y^2}{2} + y e^{-x^2} \right]_0^x \)
\( = \dfrac{x^2}{2} + x e^{-x^2} \)
Nous substituons maintenant \( I \) dans \( V \) et calculons l'intégrale donnée
\( \displaystyle V = \int _0^1 (\dfrac{x^2}{2} + x e^{-x^2} ) dx \)
\( = \left[ \frac{x^3}{6}-\frac{1}{2}e^{-x^2} \right]_0^1 \)
\( = \dfrac{2}{3} - \dfrac{1}{2}e^{-1} \)
Exemple 4
Évaluez l'intégrale double \( \displaystyle V = \iint_R \left(\sqrt{1+y^3}+\:x\right)\:dy \:dx \) sur la région \( R \) bleue comme indiqué ci-dessous.
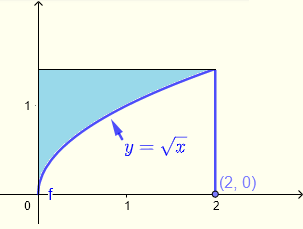
Solution de l'exemple 4
Soit l'intégrale interne \( \displaystyle I = \int \left(\sqrt{1+y^3}+\:x\right) \; dy \)
On peut facilement voir que cette intégrale n'est pas facile à faire analytiquement.
Interchangeons l'ordre d'intégration.
\( V = \displaystyle \iint_R \left(\sqrt{1+y^3}+\:x\right)\:dx \:dy \)
La région \( R \) peut être décrite par:
\( R\) : \( 0 \le x \le y^2 \) , \( 0 \le y \le \sqrt 2 \)
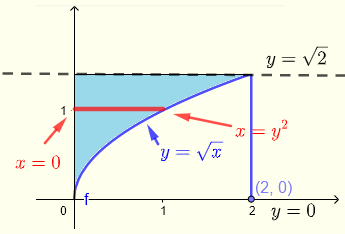
\( \displaystyle V = \int _0^{\sqrt 2} \int _0^{y^2} \left(\sqrt{1+y^3}+\:x\right) dx dy \)
Évaluons l'intégrale interne \( I \).
\( I = \displaystyle \int _0^{y^2} \left(\sqrt{1+y^3}+\:x\right) dx \)
\( = \left [ x \sqrt{1+y^3} + \dfrac{x^2}{2} \right]_0^{y^2} \)
Évaluons et simplifions
\( = y^2\sqrt{y^3
+1}+\frac{y^4}{2} \)
Substituons \( I \) dans \( V \) et calculons l'intégrale externe
\( \displaystyle V = \int _{0\:}^{\sqrt 2} \left(y^2\sqrt{y^3+1}+\frac{y^4}{2} \right) \; dy \)
Calculons l'intégrale ci-dessus
\( \displaystyle V = \left [ \frac{2}{9}\left(y^3+1\right)^{\frac{3}{2}}+\frac{y^5}{10} \right]_0^{\sqrt 2} \)
Simplifions
\( V = \frac{2}{9}\left(\left(\sqrt{2}\right)^3+1\right)^{\frac{3}{2}}+\frac{\left(\sqrt{2}\right)^5}{10}-\dfrac{2}{9} \approx 2.00 \)
Exemple 5
Évaluez l'intégrale double \( \displaystyle V = \iint_R (x+y)\:dydx \) sur la région \( R \) délimitée par les courbes des équations \( x = (y-2)^2-2 \) et \( y = - x + 6 \)
Solution de l'exemple 5
Si des bandes verticales sont utilisées, la région d'intégration aura deux parties car les limites de \( y \) sont différentes dans les intervalles \( -2 \le x \le 2 \) et \( 2 \le x \le 7 \) et les calculs de l'intégrale sont très difficiles.
Nous utilisons donc des bandes horizontales.
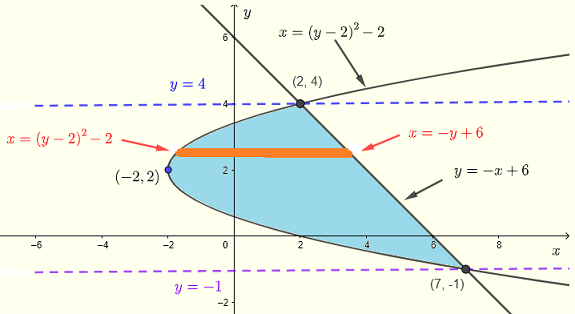
La région \( R \) peut être décrite par:
\( R\) : \( (y-2)^2 - 2 \le x \le -y+6 \) , \( -1 \le y \le 4 \)
\( \displaystyle V = \int _{-1}^{4} \int _{(y-2)^2 - 2}^{-y+6} (x+y)\:dx \: dy \)
Soit l'intégrale interne \( \displaystyle I = \int _{(y-2)^2 - 2}^{-y+6} (x+y)\:dx \)
Calculons l'intégrale ci-dessus
\( I = \dfrac{-y^4+6y^3-13y^2+12y+32}{2} \)
Substituons \( I \) dans \( V \) et calculons l'intégrale externe
\( \displaystyle V = \int _{-1}^4 \left( \dfrac{-y^4+6y^3-13y^2+12y+32}{2} \right) \; dy \)
Calculons l'intégrale ci-dessus
\( \displaystyle V = \dfrac{1}{2} \left[-\dfrac{y^5}{5}+\dfrac{3y^4}{2}-\dfrac{13y^3}{3}+6y^2+32y\right]_{-1}^4 \)
Évaluons
\( V = \dfrac{875}{12} \)
Note
À titre d'exercice, montrez qu'en utilisant des bandes verticales, l'intégrale double est donnée par:
\( \displaystyle \int _{-2}^2\:\int _{2-\sqrt{x+2}}^{2+\sqrt{x+2}}\:\left(x+y\right)dydx+\int _2^7\:\int _{2-\sqrt{x+2}}^{-x+6}\:\left(x+y\right)dydx \)
Plus de Questions avec Réponses
Partie 1
-
Écrivez les limites de l'intégrale double \( \displaystyle V = \iint_R x y \;dy \;dx \) et \( \displaystyle V = \iint_R x y \;dx \;dy \) où la région \( R \) est sur le plan \( xy\) tel que \(x \ge 0\) et \(y \ge 0\) et délimitée par la courbe dont l'équation est donnée par
\( x^2 + y^2 = 1 \) et évaluez-la.
-
Écrivez les limites de l'intégrale double \( \displaystyle V = \iint_R \sin(x^2) \;dy \;dx \) et \( \displaystyle V = \iint_R \sin(x^2) \;dx \;dy \) où la région \( R \) est un triangle avec des sommets aux points \( A(0,0)\) , \( B(3,0) \) et \( C(3,3) \) et évaluez-la.
Partie 2
Évaluez \( \displaystyle V = \int _0^1 \int _{ \arcsin y}^{\frac{\pi }{2}}\:\left(xy\right)dxdy \)
Réponses aux Questions Ci-dessus
Partie 1:
-
Région d'intégration
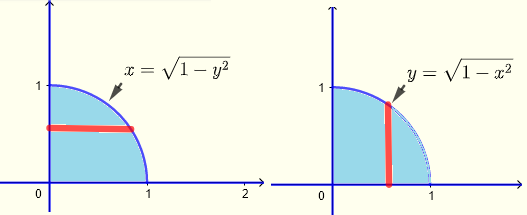
Bandes verticales
\( 0 \le x \le 1 \) , \( 0 \le y \le \sqrt{1-x^2} \)
\( \displaystyle \int _0^1\:\int _0^{\sqrt{1-x^2}}\:xy\:dy\:dx = 1/8 \)
Bandes horizontales
\( 0 \le x \le \sqrt{1-y^2} \) , \( 0 \le y \le 1 \)
\( \displaystyle \int _0^1\:\int _0^{\sqrt{1-y^2}}\:xy\:dx\:dy = 1/8\)
-
Région d'intégration

Bandes verticales
\( 0 \le x \le 3\) , \( 0 \le y \le x \)
\( \displaystyle \int _0^3\:\int _0^x \:\sin(x^2)\:dy\:dx = \dfrac{1}{2}\left(-\cos \left(9\right)+1\right) \)
Bandes horizontales
\( y \le x \le 3 \) , \( 0 \le y \le 3 \)
\( \displaystyle \int _y^3\:\int _0^3\:\sin(x^2)\:dx\:dy \) Très difficile à résoudre analytiquement.
Partie 2
\( \displaystyle V = \int _0^1 \int _{ \arcsin y}^{\frac{\pi }{2}}\:\left(xy\right)dxdy \)
Calculons l'intégrale interne \( I \) donnée par
\( \displaystyle I = \int _{ \arcsin y}^{\frac{\pi }{2}}\:\left(xy\right)dx \)
\( = y \left(\dfrac{\pi^2}{8} - \dfrac{\arcsin^2(y)}{2} \right) \)
Nous substituons maintenant \( I \) par son expression dans l'intégrale \( V \)
\( \displaystyle V = \int _0^1 (y \left(\dfrac{\pi^2}{8} - \dfrac{\arcsin^2(y)}{2} \right)) dy \)
ce qui est difficile à faire analytiquement.
Recommençons et échangeons maintenant l'ordre d'intégration
Commencez par tracer la région \( R \) d'intégration
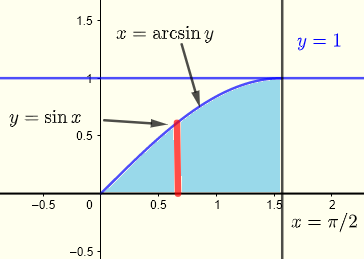
\( \displaystyle V = \int _0^{\frac{\pi }{2}} \int _0^{\sin x} x \; y \; dy \;dx \)
Soit l'intégrale interne \( I = \int _0^{\sin x} x \; y \; dy \)
Calculons \( I \)
\( I = x\frac{\sin ^2\left(x\right)}{2} \)
\( \sin^2(x) = \dfrac{1-\cos(2x)}{2} \)
\( I =
\dfrac{x}{4}(1-cos(2x) \)
Substituons \( I \) dans \( V \)
\( \displaystyle V = \int _0^{\frac{\pi }{2}} (\dfrac {x}{4} - \dfrac {x}{4} \cos (2x) ) dx \)
Divisons l'intégrande
\( \displaystyle = \int _0^{\frac{\pi }{2}} \dfrac {x}{4} dx - \int _0^{\frac{\pi }{2}} \dfrac {x}{4} \cos (2x) dx \)
L'intégrale à droite est effectuée en utilisant la technique d'intégration par parties pour obtenir
\( = \left[ \frac{x^2}{8} \right]_0^{\pi/2}- \left[\frac{1}{8} x \sin (2x)+\frac{1}{16}\cos (2x) \right]_0^{\pi/2} \)
Évaluons
\( = \dfrac{\pi^2+4}{32} \)
Plus de Références et Liens
- Calculs d'Intégrales Doubles
- Howard Anton, Irl C. Bivens, Stephen Davis ; Calculus: Early Transcendentals; Willey, 2012.
- Gilbert Strang; MIT, Calculus, Wellesley-Cambridge Press, 1991
- Joel Hass, University of California, Davis; Maurice D. Weir Naval Postgraduate School; George B. Thomas, Jr.Massachusetts Institute of Technology ; University Calculus , Early Transcendentals, Third Edition
, Boston Columbus , 2016, Pearson.
Mathématiques pour les Ingénieurs avec des Exemples et Solutions