Résoudre les Problèmes de Circuits a CA avec Solutions

Table des Matières

Les lois de Kirchhoff et d'Ohm sont étendues et utilisées pour résoudre les problèmes de circuits AC en utilisant des impédances sous forme complexe.
Toutes les grandeurs telles que les tensions, les courants et les impédances sont représentées par des nombres complexes sous forme standard et polaire.

Revue des Nombres Complexes

L'unité imaginaire est définie par \( j = \sqrt {-1} \) ou \( j^2 = - 1 \)
Un nombre complexe \( Z \) dans la forme standard \( Z = a + j b \) peut être écrit sous forme polaire comme
\( Z = r \; \angle \; \theta \)
où \( r \) et \( \theta \) sont le module et argument de \( Z \), respectivement et sont définis par
\( r = |Z| = \sqrt {a^2 + b^2} \) et \( \theta = \arctan \left( \dfrac{b}{a} \right) \) dans l'intervalle \( -\pi \lt \theta \le \pi \)
Il est plus facile de diviser ou multiplier des nombres complexes en forme polaire
Soit \( Z_1 = r_1 \; \angle \; \theta_1 \) et \( Z_2 = r_2 \; \angle \; \theta_2 \)
\( Z_1 \cdot Z_2 = r_1 \cdot r_2 \; \angle \; \theta_1 + \theta_2 \)
\( \dfrac{Z_1}{Z_2} = \dfrac{r_1}{r_2} \; \angle \; \theta_1 - \theta_2 \)

Problèmes avec Solutions

Problème 1
Trouver l'amplitude et le déphasage (sous forme polaire) du courant à travers et des tensions aux bornes de la résistance \( R \) et du condensateur \( C \) dans le circuit ci-dessous étant donné que la source de tension \( v_i = 10 \cos (\omega t ) \) V, les résistances \( R = 100 \; \Omega \), \( C = 0.47 \; \mu F \), fréquence \( f = 1 \) kHz et \( \omega = 2 \pi f \).

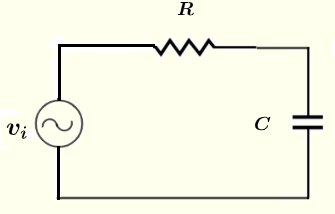
Solution au Problème 1
Soient \( V_i \), \( V_R \) \( V_C \) et \( I \) les formes complexes de \( v_i \), \( v_R \) \( v_C \) et \( i \) respectivement.


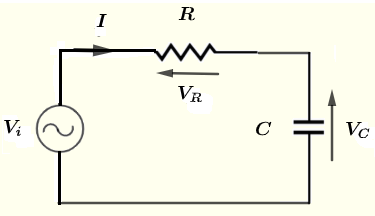
Utilisez la loi de Kirchhoff des tensions autour de la boucle pour écrire l'équation
\( V_i - V_R - V_C = 0\)      (1)
Les impédances complexes de la résistance \( R \) et du condensateur \( C \) sont données par
\( Z_R = R \; \)       (réel)
\( Z_C = - j \dfrac{1}{\omega C} \; \)       (imaginaire)

Utilisez la loi d'Ohm pour écrire
\( V_R = Z_R I \) et \( V_C = Z_C I \)
Remplacez \( V_R \) et \( V_C \) par leur expression dans l'équation (1)
\( V_i - Z_R I - Z_C I = 0 \)
Résolvez ce qui précède pour \( I \)
\( I = \dfrac{V_i}{Z_R + Z_C} \)

Calculez \( V_R \) et \( V_C \) en utilisant la loi d'Ohm comme suit
\( V_R = Z_R I = \dfrac{V_i Z_R }{Z_R + Z_C} \)

\( V_C = Z_C I = \dfrac{V_i Z_C }{Z_R + Z_C} \)


Sous forme polaire complexe, \( v_i = 10 \cos (\omega t ) \) peut être écrit comme
\( V_i = 10 \; \angle \; 0 \)

Nous substituons maintenant \( V_i \), \( Z_R \) et \( Z_C \) par leurs expressions ci-dessus pour obtenir
\( I = \dfrac{10 \; \angle \; 0}{R - j \dfrac{1}{\omega C}} \)

\( V_R = \dfrac{10 R \; \angle \; 0 \; }{R - j \dfrac{1}{\omega C}} \)

\( V_C = \dfrac{ (10 \; \angle \; 0 \;) (- j \dfrac{1}{\omega C}) }{R - j \dfrac{1}{\omega C}} \)

Soit le dénominateur de toutes les expressions ci-dessus \( Z_D = R - j \dfrac{1}{\omega C} \) et réécrivons-le sous forme complexe
Module de \( Z_D \) : \( | Z_D | = \sqrt {R^2 + \dfrac{1}{\omega^2 C^2}} \)

Argument de \( Z_D \) : \( \phi = \arctan \dfrac{-\dfrac{1}{\omega C}}{R} = \arctan \dfrac{-1}{R \omega C} \)

Nous réécrivons maintenant la quantité complexe \( - j \dfrac{1}{\omega C} \) sous forme polaire
\( - j \dfrac{1}{\omega C} = \dfrac{1}{\omega C} \; \angle \; -\dfrac{\pi}{2} \)

Nous substituons maintenant toutes les quantités complexes dans \( I \), \( V_R \) et \( V_C \) par leur forme polaire et réécrivons
\( I = \dfrac{10 \; \angle \; 0}{{ | Z_D | \; \angle \; \phi}} \)

\( V_R = \dfrac{10 R \; \angle \; 0 \; }{ | Z_D | \; \angle \; \phi} \)

\( V_C = \dfrac{10 \; \angle \; 0 \; (\dfrac{1}{\omega C} \; \angle \; -\dfrac{\pi}{2}) }{{ | Z_D | \; \angle \; \phi}} \)

Simplifiez ce qui précède

\( I = \dfrac{10} { | Z_D | } \; \angle \; - \phi \)

\( V_R = \dfrac{10 R}{ | Z_D |} \; \angle \; - \phi \)

\( V_C = \dfrac{10}{ \omega C | Z_D | } \; \angle \; -\dfrac{\pi}{2}- \phi \)

Nous substituons maintenant toutes les quantités connues par leurs valeurs numériques
\( \omega = 2 \cdot \pi \cdot f = 2 \cdot \pi 10^3 = 2000 \pi \)
\( | Z_D | = \sqrt {R^2 + \dfrac{1}{\omega^2 C^2}} = \sqrt {100^2 + \dfrac{1}{(2000 \pi)^2 (0.47 \cdot 10^{-6})^2}} = 353.08 \; \Omega \)
\( \phi = \arctan \dfrac{-\dfrac{1}{\omega C}}{R} = \arctan \dfrac{-\dfrac{1}{2000 \pi \cdot 0.47 \cdot 10^{-6} }}{100} = -73.55^{\circ} \)
Ainsi

\( I = \dfrac{10} { | Z_D | } \; \angle \; - \phi = 0.0283 \; \angle \; 73.55^{\circ} \)
L'amplitude de \( I \) est \( 0.02832 \; A\) et le déphasage est \( 73.55^{\circ} \)

\( V_R = \dfrac{10 R}{ | Z_D |} \; \angle \; - \phi = 2.832 \; \angle \; 73.55^{\circ} \)
L'amplitude de \( V_R \) est \( 2.832 \; V\) et le déphasage est \( 73.55^{\circ} \)

\( V_C = \dfrac{10}{ \omega C | Z_D | } \; \angle \; -\dfrac{\pi}{2}- \phi = 9.591 \; \angle \; -16.45^{\circ} \)
L'amplitude de \( V_C \) est \( 9.591 \; V\) et le déphasage est \( -16.45^{\circ} \)

Problème 2

Trouvez l'amplitude et le déphasage (forme polaire) de la tension \( v_o \) dans le circuit ci-dessous, sachant que la source de tension \( v_i = 10 \cos (\omega t ) \; V \), les résistances \( R = 100 \; \Omega \), \( C = 0.47 \; \mu F \), \( L = 300 \; mH \), la fréquence \( f = 2 \) kHz et \( \omega = 2 \pi f \).


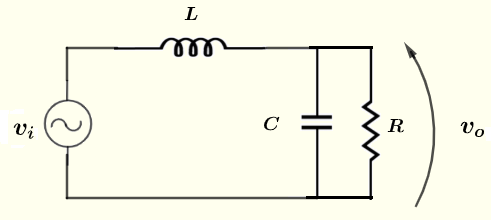
Solution du Problème 2
Soient \( I \), \( V_i \) et \( V_0 \) les formes complexes de \( i \), \( v_i \) et \( v_o \) respectivement.
\( V_i \) peut être écrit sous forme polaire comme suit
\( V_i = 10 \; \angle \; 0 \)
Les impédances de la résistance \( R \) sont données par
\( Z_R = R \; \)
Les impédances de la capacité \( C \) sont données par
\( Z_C = - j \dfrac{1}{\omega C} \; \)
La résistance \( R \) et la capacité \( C \) sont en parallèle. L'impédance \( Z \) équivalente à \( R \) et \( C \) est donnée par

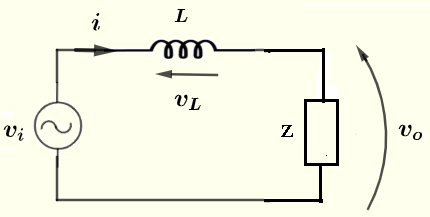
\( Z = \dfrac{Z_R \cdot Z_C}{Z_R + Z_C} \)
L'inductance \( L \) a une impédance complexe \( Z_L \) donnée par
\( Z_L = j \omega L \)
Utilisez la loi de Kirchhoff des tensions autour de la boucle pour écrire l'équation
\( V_i - V_L - V_0 = 0\)      (1)
Utilisez la loi d'Ohm pour écrire
\( V_L = Z_L I \) et \( V_0 = Z I \)
Substituez \( V_L \) et \( V_0 \) par leur expression dans l'équation (1)
\( V_i - Z_L I - Z I = 0 \)
Résolvez pour \( I \)
\( I = \dfrac{V_i}{ Z_L + Z} \)
Utilisez la loi d'Ohm pour écrire
\( V_o = Z I = \dfrac{Z}{ Z_L + Z} V_i\)
Remplacez par les quantités connues pour trouver les valeurs numériques
\( \omega = 2 \pi f = 2 \pi \cdot 2000 = 4000 \pi \)
\( Z_R = R = 100 \)
\( Z_C = - j \dfrac{1}{\omega C} = - j \dfrac{1}{4000 \pi \cdot 0.47 \cdot 10^{-6}} = - 169.314 j \)

\( Z = \dfrac{R \cdot Z_C}{R + Z_C} \) ( (\( R \) et \( C \) en parallèle )

\( = \dfrac{100 \cdot (- 169.314 j)}{100 - 169.314 j } = 74.138 -43.787 j\)
et
\( Z_L = j \omega L = 4000 \pi \cdot 300 \cdot 10^{-3} j = 3769.911 j \)
\( V_o = \dfrac{Z}{ Z_L + Z} V_i \)

\( = \dfrac{Z}{ Z_L + Z} V_i \)

\( = \dfrac{74.138 -43.787 j}{ 3769.911 j + 74.138 -43.787 j} V_i \)
Simplifiez
\( = (-0.01135 -0.02012 j) V_i \)
Écrivez le nombre complexe \( (-0.01135 -0.02012 j) \) sous forme polaire et remplacez \(V_i \) par ses valeurs sous forme polaire données ci-dessus.
\( = ( 0.02310 \angle -119.43^{\circ} ) (10 \; \angle \; 0) \)
Simplifiez
\( V_o = 0.23 \; \angle \; -119.43^{\circ} \)

Problème 3

Trouvez l'amplitude et le déphasage (forme polaire) de la tension \( v_o \) dans le circuit ci-dessous, sachant que la source de tension \( v_i = 10 \cos (\omega t ) \; V \), les résistances \( R_1 = 220 \; \Omega \), \( R_2 = 2.2 \; k\Omega \), \( R_3 = 1 \; k\Omega \), \( C_1 = 0.47 \; \mu F \), \( C_2 = 1.5 \; \mu F \), \( L = 30\; mH \), la fréquence \( f = 2.5 \) kHz et \( \omega = 2 \pi f \).

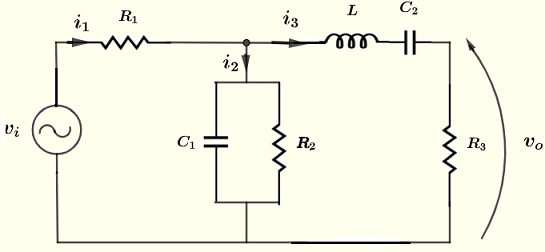
Solution du Problème 3
Soient \( I_1 \), \( I_2 \), \( I_3 \), \( V_i \) et \( V_0 \) les formes complexes de \( i_1 \) , \( i_2 \), \( i_3 \) , \( v_i \) et \( v_o \) respectivement.
\( V_i \) peut être écrit sous forme polaire comme suit
\( V_i = 10 \; \angle \; 0 \)
\( V_o \) peut être calculé en utilisant la loi d'Ohm
\( V_o = R_3 I_3\)
Nous devons donc calculer \( I_3 \)
Regroupons les impédances, comme indiqué dans le circuit ci-dessous, de telle sorte que
\( Z_1 = R_1 \)
\( Z_2 = \dfrac{R_2 ( - \dfrac{1}{\omega C_1} j)}{R_2 - \dfrac{1}{\omega C_1} j} \)      ( \( C_1 \) et \( R_2 \) sont en parallèle)
\( z_3 = R_3 + j \omega L - \dfrac{1}{ \omega C_2} j \)      ( \( C_2 \), \( L \) et \( R_3 \) sont en série)

La loi de Kirchhoff des tensions appliquée aux deux boucles fermées donne 2 équations
\( V_i - V_{z_1} - V_{z_2} = 0 \)
\( V_{z_2} - V_{z_3} = 0 \)
Appliquez la loi d'Ohm pour écrire \( V_{z_1} = Z_1 I_1 \), \( V_{z_2} = Z_2 I_2 \) et \( V_{z_3} = Z_3 I_3 \) et substituez dans les équations ci-dessus pour obtenir des équations ne contenant que des courants.
\( V_i - Z_1 I_1 - Z_2 I_2 = 0 \)     (1)
\( Z_2 I_2 - Z_3 I_3 = 0 \)     (2)
Nous utilisons maintenant la loi de Kirchhoff du courant au nœud A pour écrire
\( I_1 = I_2 + I_3 \)     (3)
Nous avons 3 équations avec trois inconnues \( I_1 \), \( I_2 \) , et \( I_3 \), mais nous avons seulement besoin de \(I_3\).
Utilisez l'équation (3) pour substituer \( I_1 \) dans l'équation (1) par \( I_2 + I_3 \) et donc éliminer \( I_1 \) des équations pour obtenir un système de deux équations et deux inconnues.
\( V_i - Z_1 ( I_2 + I_3) - Z_2 I_2 = 0 \)     (4)
\( Z_2 I_2 - Z_3 I_3 = 0 \)     (5)
Réécrivez le système d'équations ci-dessus sous forme standard
\( (Z_1 + Z_2 ) I_2 + Z_1 I_3 = V_i \)     (4)
\( Z_2 I_2 - Z_3 I_3 = 0 \)     (5)
Utilisez le déterminant pour résoudre le système d'équations ci-dessus
\( I_3 = \dfrac{\begin{vmatrix} Z_1 + Z_2 & V_i \\ Z_2 & 0 \end{vmatrix}}{\begin{vmatrix} Z_1 + Z_2 & + Z_1 \\ Z_2 & -Z_3 \end{vmatrix}} \)
Évaluez les déterminants pour trouver
\( I_3 = \dfrac{Z_2}{(Z_1+Z_2)Z_3 + Z_1 Z_2} V_i \)

Calculs Numériques
\( \omega = 2 \pi f = 5000 \pi \)
\( Z_1 = 220 \)
\( Z_2 = \dfrac{2200 ( - \dfrac{1}{5000 \pi \cdot 0.47 10^{-6}} j)}{2200 - \dfrac{1}{5000 \pi \cdot 0.47 10^{-6}} j} \)

\( Z_2 = 8.30804 -134.93950 j \)

\( z_3 = 1000 + 5000 \pi \cdot 30 \cdot 10^{-3} j - \dfrac{1}{ 5000 \pi \cdot 1.5 \cdot 10^{-6}} j \)
\( Z_3 = 1000 + 428.79757 j \)
\( I_3 = (0.00013 - 0.00043 j)V_i = 0.00044 \angle -73.18^{\circ} \cdot 10 \angle 0\)
\( V_0 = R_3 I_3 = 1000 \cdot 0.00044 \angle -73.18^{\circ} \cdot 10 \angle 0 \)
Simplifiez
\( V_0 = 4.4 \angle -73.18^{\circ} V \)

Plus de Problèmes avec Réponses

Problème 4
Étant donné \( v_i = 10 \angle 0^{\circ} \) , \( R = 200 \; \Omega \), \( C = 0.47 \; \mu F \), \( L = 40 \; mH \) , fréquence \( f = 1 \) kHz.
Trouvez le courant \( I \) à travers et la tension \( V_0 \) aux bornes de l'inductance sous forme complexe.

Réponse au Problème 4

Réponse: \( I = 0.047 \angle -47.84^{\circ}\) , \(V_0 = 11.38 \angle 42.16^{\circ} \)

Problème 5
Étant donné \( v_i = 10 \angle 0^{\circ} \) , \( R_1 = 100 \; \Omega \), \( C = 0.47 \; \mu F \), \( R_2 = 120 \; \Omega \), \( R_3 = 200 \; \Omega \), \( R_4 = 400 \; \Omega \), \( L = 20 \; mH \) , fréquence \( f = 2 \) kHz.
Trouvez les courants \( I_1 \), \( I_2 \) , \( I_3 \) et les tensions à travers chaque résistance sous forme complexe.

Réponse au Problème 5
Réponses
Courants: \( I_1 = 0.054 \angle 10.55^{\circ} \; , \; I_2 = 0.048 \angle 23.01^{\circ} \; , \; I_3 = 0.013 \angle -42.22^{\circ} \)
Tensions: \( V_{R_1} = 5.49 \angle 10.55^{\circ} \; , \; V_{R_2} = 4.71 \angle -12.32^{\circ} \; , \; V_{R_3} = 2.60 \angle -42.22^{\circ} \; , \; V_{R_4} = 2.77 \angle 15.63^{\circ} \)

Plus de Références et Liens