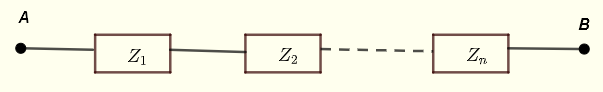
L'impédance équivalente entre les points A et B est donnée par
\[ Z_{AB} = Z_1 + Z_2 + ... + Z_n\]
On discute ici comment les impédances complexes sont utilisées pour calculer les impédances équivalentes en série et en parallèle dans les circuits AC. Toutes les étapes sont présentées en utilisant des calculs symboliques puis des valeurs numériques sont utilisées.
Parce que le symbole \( i \) est utilisé pour les courants dans les circuits AC, ici nous utilisons \( j \) comme l'unité imaginaire définie par \( j^2 = -1 \) ou \( j = \sqrt{-1} \)
Soit \( Z_1 \) , \( Z_2 \) ... \( Z_n \) des impédances en série comme montré ci-dessous.
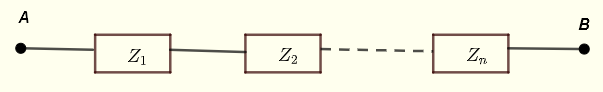
L'impédance équivalente entre les points A et B est donnée par
\[ Z_{AB} = Z_1 + Z_2 + ... + Z_n\]
Exemple 1
Trouver l'impédance complexe équivalente au circuit RLC en série ci-dessous étant donné :
Fréquence \( f = 1 \; kHz \) , \( C = 10 \; \mu F \) , \( L = 10 \; mH \) et \( R = 100 \; \Omega \)

Solution aux Problèmes 1
Soit
\( Z_R = R \) , \( Z_C = \dfrac{1}{j \omega C} = \dfrac{-j}{\omega C} \) , \( Z_L = j \omega L\)
Appliquer la règle des impédances des circuits en série
\( Z_{AB} = Z_R + Z_C + Z_L = R - \dfrac{j}{\omega C} + j \omega L \)
Soit
\( X_L = \omega L = 2 \pi f L \) et \( X_C = \dfrac{1}{\omega C} = \dfrac{1}{2 \pi f C} \)
et réécrire \( Z_{AB} \) comme suit
\( Z_{AB} = R + j(X_L - X_C) \)
Remplacer par les valeurs numériques
\( X_L = \omega L = 2 \pi f L = 2 \pi 10^3 10^{-2} = 62.83 \Omega \)
\( X_C = \dfrac{1}{\omega C} = \dfrac{1}{2 \pi f C} = \dfrac{1}{2 \pi 10^3 10^{-5} } = 15.92 \Omega \)
Regrouper les termes imaginaires
\( Z_{AB} = 100 + j ( 62.83 - 15.92 ) \)
Simplifier
\( Z_{AB} = 100 + j ( 62.83 - 15.92 ) = 100 + 46.91 j\)
Écrire ce qui précède sous forme exponentielle
\( Z_{AB} = \sqrt {100^2 + 46.91^2} e^{j \arctan{\dfrac{46.91}{100}}} = 110.45 e^{j 0.44} \)
\( Z_{AB} \) écrit sous forme de phaseur
\( Z_{AB} = 110.45 \angle 0.44 \; rad = 110.45 \angle 25.13^{\circ} \)
Un calculateur d'impédance de circuit RLC en série peut être utilisé pour plus de pratiques.
Soit \( Z_1 \) , \( Z_2 \) ... \( Z_n \) des impédances en parallèle comme montré ci-dessous.
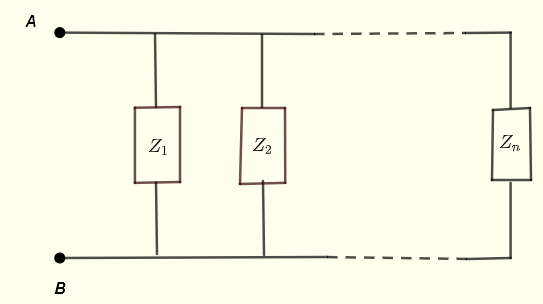
L'impédance équivalente entre les points A et B est donnée par
\[ \dfrac{1}{Z_{AB}}
= \dfrac{1}{Z_1} + \dfrac{1}{Z_2} + ... + \dfrac{1}{Z_n} \]
Exemple 2
Trouver l'impédance complexe équivalente au circuit RLC en parallèle ci-dessous étant donné :
Fréquence \( f = 1.5 \; kHz \) , \( C = 15 \; \mu F \) , \( L = 20 \; mH \) et \( R = 50 \; \Omega \)

Solution aux Problèmes 2
Soit
\( Z_R = R \) , \( Z_C = \dfrac{1}{j \omega C} \) , \( Z_L = j \omega L\)
Appliquer la règle des impédances des circuits en parallèle
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{Z_R} + \dfrac{1}{Z_C} + \dfrac{1}{Z_L} \)
\( = \dfrac{1}{R} + \dfrac{1}{\dfrac{1}{j \omega C}} + \dfrac{1}{j \omega L} \)
Soit
\( X_L = \omega L \) et \( X_C = \dfrac{1}{\omega C} \)
et réécrire ce qui précède comme
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{R} + \dfrac{1}{\dfrac{X_C}{j}} + \dfrac{1}{j X_L} \)
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{R} + \dfrac{j}{{X_C}} - j \dfrac{1}{ X_L} \)
\( = \dfrac{1}{R} + j (\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} ) \)
Le module \( r \) du nombre complexe ci-dessus est donné par
\( r = \sqrt { (\dfrac{1}{R})^2 + (\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} )^2} \)
et son argument \( \alpha \) est donné par
\( \alpha = \arctan \left(\dfrac{\dfrac{1}{{X_C}} - \dfrac{1}{ X_L}}{\dfrac{1}{R}} \right) \)
\( = \arctan \left(\dfrac{R}{X_C}-\dfrac{R}{X_L} \right) \)
Nous utilisons maintenant la forme exponentielle du nombre complexe pour écrire
\( \dfrac{1}{Z_{AB}} = r e^{j\alpha} \)
Nous écrivons maintenant l'impédance équivalente \( Z_{AB} \) sous forme d'un nombre complexe en forme exponentielle
\( Z_{AB} = \dfrac{1}{r} e^{-j \alpha} \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} e^{-j \arctan \left(\dfrac{R}{X_C}-\dfrac{R}{X_L} \right) } \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} e^{j \arctan \left(\dfrac{R}{X_L}-\dfrac{R}{X_C} \right) } \)
Nous utilisons maintenant les valeurs données
\( f = 1.5 \; kHz \) , \( C = 15 \; \mu F \) , \( L = 20 \; mH \) et \( R = 50 \; \Omega \)
\( X_L = \omega L = 2 \pi f L = 2 \pi 1.5 \times 10^3 \times 20 10^{-3 } = 188.50 \)
\( X_C = \dfrac{1}{\omega C} = \dfrac{1}{ 2\pi f C} = \dfrac{1}{ 2\pi 1.5 \times 10^3 \times 15 10^{-6}} = 7.07\)
Module: \( \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{50}\right)^2 + \left(\dfrac{1}{{7.07}} - \dfrac{1}{ 188.50} \right)^2}} \)
\( = 7.27 \)
Argument: \( \arctan \left(\dfrac{R}{X_L}-\dfrac{R}{X_C} \right) \)
\( = \arctan \left(\dfrac{50}{188.50}-\dfrac{50}{7.07} \right) \)
\( = - 81.64^{\circ} \)
Un calculateur d'impédance de circuit RLC en parallèle peut être utilisé pour plus de pratiques.