Circuit RLC Série Résonant

Table des Matières

Résonant circuits RLC série et les formules de la fréquence de résonance , les fréquences de coupure sont développées, la largeur de bande et le facteur de qualité sont définis et tous sont utilisés dans des exemples avec des solutions détaillées. \( \) \( \) \( \) \( \)
Dans ce qui suit, la lettre majuscule \( I \) est la forme complexe (polaire) du courant réel \( i \) et la lettre majuscule \( V_i \) est la forme complexe (polaire) de la tension réelle \( v_i \).
Un calculateur de circuit RLC série résonant peut être utilisé pour vérifier les calculs des exemples ci-dessous et également pour plus de pratique et d'investigations de ces circuits.

A - Circuit RLC série résonant

Considérez le circuit RLC série représenté ci-dessous.

Pour un circuit alimenté par une source de tension de fréquence \( f \), l'impédance totale \( Z \) du circuit RLC série est donnée par :
\[ Z = R + j \left(\omega L - \dfrac{1}{\omega C} \right) \]
La relation entre le courant \( I \) et la tension \( V_i \) est donnée par
\[ I = \dfrac{V_i}{Z} \]
où \( V_i \) et \( I \) sont la forme complexe de la tension \( v_i \) et du courant \( i \) respectivement.
En utilisant la définition de la magnitude d'un nombre complexe, la magnitude \( |Z| \) est donnée par
\( |Z| = \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} \)
Si \( V_0 \) est la valeur de crête de la source de tension \( v_i = V_0 \cos (\omega t) \), alors la valeur de crête \( I_0 \) de \( I \) est donnée par
\( I_0 = \dfrac{V_0}{ |Z| } = \dfrac{V_0}{ \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} } \)
La fréquence de résonance est définie comme la fréquence pour laquelle \( I_0 \) est maximum ou lorsque la magnitude de \( Z \) est minimum.
Puisque la résistance \( R \) est indépendante de la fréquence, la valeur minimale de \( |Z| \) se produit à \( \omega = \omega_r \) tel que
\( \left(\omega_r L - \dfrac{1}{\omega_r C} \right) = 0 \)
Résoudre l'équation ci-dessus pour \( \omega_r \) pour obtenir la fréquence de résonance
\[ \omega_r = \dfrac{1}{\sqrt {L C}} \quad \quad (I) \]
À la fréquence de résonance \( \omega = \omega_r \), nous avons :
1) \( Z = R \)
Pour \( V_0 \), la valeur de crête de la source de tension \( v_i \), la valeur de crête \( I_0 \) de \( I \) est donnée par
2) \( I_0 = \dfrac{V_0}{R} \)
Soit \( X_L = \omega L \) et \( X_C = \dfrac{1}{\omega C} \)
3) \( X_L = X_C \)

Exemple 1
Soit \( R=300 \; \Omega \), \( L = 100 \; mH \) et \( C = 100 \mu F \) dans le circuit RLC série ci-dessus .
a) Trouvez la fréquence de résonance \( \omega_r \)
b) Tracez \( |Z| \), \( X_L = \omega L \), \( X_C = \dfrac{1}{\omega C} \) et \( I_0 \) en fonction de la fréquence \( \omega \) et discutez des graphiques obtenus.

Solution à l'Exemple 1
a)
La fréquence de résonance \( \omega_r \) est donnée par
\( \omega_r = \dfrac{1}{\sqrt {L C}} = \dfrac{1}{\sqrt{100\times10^{-3} \times 100 \times 10^{-6}}} \approx 316.23\)
b)
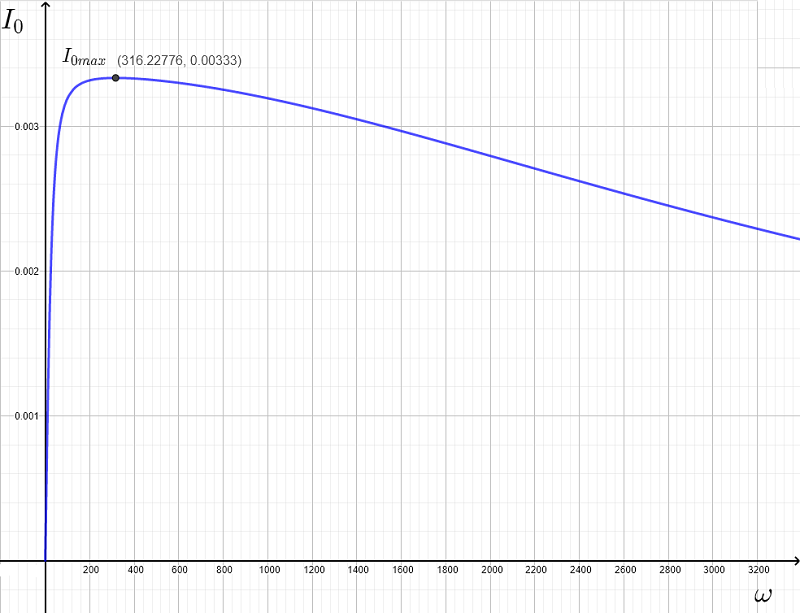
Ci-dessous sont représentés les graphiques de \( |Z| \), \( X_L \) et \( X_C \).
D'après les graphiques, \( |Z| \) a une valeur minimale égale à \( R = 300 \; \Omega \) (point A)
Les graphiques de \( X_L \) et \( X_C \) se croisent (point B) et sont donc \( X_L = X_C \) ou \( \left(\omega_r L - \dfrac{1}{\omega_r C} \right) = 0 \) .



Sur le graphique ci-dessous est représenté le courant \( I_0 \) et il est maximum à la fréquence de résonance \( \omega_r \approx 316.23\) (après arrondi à 2 décimales)

B - Puissance Moyenne dans un Circuit Résonant

La puissance moyenne \( P_a \) délivrée au circuit RLC série est donnée par : \[ \displaystyle \quad \quad P_a = \dfrac{V_0^2}{2 |Z|} \cos \theta \quad \quad (II) \] où \( \theta \) est l'argument de l'impédance \( Z = R + j \left(\omega L - \dfrac{1}{\omega C} \right) \) et est donné par
\( \theta = \arctan \left( \dfrac{ \omega L - \dfrac{1}{\omega C} }{R} \right) \)
En utilisant les propriétés des fonctions trigonométriques inverses, nous avons
\( \tan \theta = \left( \dfrac{ \omega L - \dfrac{1}{\omega C} }{R} \right) \)
\( \theta \) peut être supposé être un angle aigu d'un triangle rectangle comme illustré ci-dessous. (Utilisez la définition de la tangente d'un angle dans un triangle rectangle et voyez que vous pouvez obtenir \( \tan \theta \) tel que défini ci-dessus.



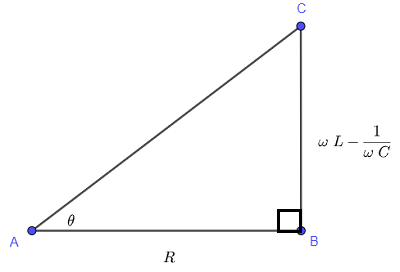
Nous utilisons maintenant le même triangle et calculons le facteur de puissance \( \cos \theta \)
L'hypoténuse du triangle est calculée comme suit
\( AC = \sqrt {R^2 + \left( \omega L - \dfrac{1}{\omega C} \right)^2} \)
\( \cos \theta = \dfrac{AB}{AC} = \dfrac{R}{\sqrt {R^2 + \left( \omega L - \dfrac{1}{\omega C} \right)^2}} \)
Substituez \( \cos \theta \) et \( |Z| \) dans la formule (II) donnée ci-dessus et exprimez la puissance \( P_a \) comme
\( \displaystyle \quad \quad P_a = \dfrac{V_0^2}{2 \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} }\dfrac{R}{\sqrt {R^2 + \left( \omega L - \dfrac{1}{\omega C} \right)^2}} \)
Simplifiez
\[ \displaystyle \quad \quad P_a = \dfrac{V_0^2 R}{2 \left({R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} \right) } \quad \quad (III) \]
À la fréquence de résonance \( \omega_r = \dfrac{1}{\sqrt {LC}} \), nous avons \( \left(\omega_r L - \dfrac{1}{\omega_r C} \right) = 0 \) et donc la puissance est maximale et égale à \[ P_{a max} = \dfrac{V_0^2}{2 \; R} \quad \quad (IV) \]

C - Fréquences de Coupure d'un Circuit Résonant et Le Facteur de Qualité

Nous définissons maintenant les fréquences de coupure comme les fréquences \( \omega_c \) pour lesquelles la puissance \( P_a(\omega) \) en (III) est la moitié de la puissance maximale \( P_{a max} \) en (IV).
Nous devons donc résoudre l'équation
\( P_a (\omega_c ) = \dfrac{1}{2} \left(\dfrac{V_0^2}{2 \; R} \right) \)

\( \dfrac{V_0^2 R}{2 \left({R^2 + \left(\omega_c L - \dfrac{1}{\omega_c C} \right)^2} \right) } = \dfrac{1}{2} \dfrac{V_0^2}{2 \; R} \)
Simplifiez pour obtenir
\( \dfrac{ R}{2 \left({R^2 + \left(\omega_c L - \dfrac{1}{\omega_c C} \right)^2} \right) } = \dfrac{1}{4 R} \)
Croisez-multiplication, simplifiez et réécrivez l'équation ci-dessus comme
\( (\omega_c L - \dfrac { 1}{\omega_c C } ) = R^2 \)
Résolvez en extrayant la racine carrée pour obtenir deux équations
\( \omega_c L - \dfrac {1}{\omega_c C} = \pm R \)
Multipliez tous les termes par \( \omega_c C \) et simplifiez
\( \omega_c^2 L C \pm \omega_c R C - 1 = \pm \omega_c R C \)
Réécrivez sous forme d'équations quadratiques dans des formes standard
\( \omega_c^2 L C \pm \omega_c R C - 1 = 0\)
Résolvez la première équation quadratique \( \quad \omega_c^2 L C + \omega_c R C - 1 = 0\)
pour obtenir deux solutions
\( \omega_{c1} = \dfrac {- R C \pm \sqrt{ (R C)^2 + 4 L C }}{ 2 L C } \)

Résolvez la deuxième équation quadratique \( \quad \omega_c^2 L C - \omega_c R C - 1=0\)
pour obtenir deux solutions
\( \omega_{c2} = \dfrac {R C \pm \sqrt{ (R C)^2 + 4 L C}}{ 2 L C } \)
Nous avons un total de 4 solutions. Remarquez que la quantité \( \sqrt{ (R C)^2 + 4 L C } \) est plus grande que \( RC \) et donc seules deux solutions sont valides puisque la fréquence de coupure est une quantité positive.
Les fréquences de coupure \( \omega_{c1} \) et \( \omega_{c2} \) sont les deux solutions données
\( \omega_{c1} = \dfrac {- R C + \sqrt{ (R C)^2 + 4 L C }}{ 2 L C } \)

\( \omega_{c2} = \dfrac {R C + \sqrt{ (R C)^2 + 4 L C}}{ 2 L C } \)
Nous avons déjà trouvé la fréquence de résonance \( \omega_r = \dfrac{1}{\sqrt{LC}} \)
Utilisez l'algèbre simple pour réécrire \( \omega_{c1} \) et \( \omega_{c1} \) en termes de \( \omega_r \)
\[ \omega_{c1} = - \dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} \quad \quad (V) \]
\[ \omega_{c2} = \dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} \quad \quad (VI) \]

Remarque que
\[ \omega_{c1} \times \omega_{c2} = \omega_r^2 \quad \quad (VII) \]

La largeur de bande du circuit résonant est définie par : \( \Delta \omega = \omega_{c2} - \omega_{c1} \)

Le facteur de qualité \( Q \) est défini par
\( Q = \dfrac{\omega_r}{\Delta \omega} \)
Substituez
\( Q = \dfrac {\omega_r} { \left(\dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} - \left(-\dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} \right) \right)} \)
Simplifiez
\[ Q = \omega_r \dfrac{L}{R} \quad \quad (VIII) \]

D - Plus d'exemples avec des solutions détaillées

Exemple 3
Un circuit résonant RLC série doit être conçu de manière à avoir les fréquences \( f_{c_1} = 650 \) Hertz et \( f_{c_2} = 950 \) Hertz comme fréquences de coupure inférieure et supérieure.
a) Calculez la capacité du condensateur \( C \) et l'inductance de l'inducteur \( L \) si la résistance de la résistance \( R \) est égale à \( 30 \Omega \).
b) Quel est le facteur de qualité du circuit ?

Solution de l'Exemple 3
a)
Calculez les fréquences angulaires.
\( \omega_{c_1} = 2 \pi f_{c_1} = 1300 \pi \) rad/s
\( \omega_{c_2} = 2 \pi f_{c_1} = 1900 \pi \) rad/s
Utilisez la formule (VII) développée ci-dessus
\( \omega_{c_1} \times \omega_{c_2} = \omega_{r}^2 \) pour calculer la fréquence de résonance \( \omega_{r} \) du circuit.
\( \omega_{r} = \sqrt {\omega_{c_1} \times \omega_{c_2}} = \sqrt {1300 \pi \times 1900 \pi } = 100 \sqrt{247} \pi = 4937.400 \) rad/s
\( \omega_{c_2} - \omega_{c_1} = \dfrac{R}{L} \)
Donc
\( L = \dfrac{R } {\omega_{c_2} - \omega_{c_1}} = \dfrac{30} {1900 \pi - 1300 \pi } = 0.01591 \) H
\( \omega_{r} = \dfrac{1}{\sqrt {L C} } \)
Donc
\( C = \dfrac{1}{\omega_{r}^2 L} = \dfrac{1}{(100 \sqrt{247} \pi)^2 \times 0.01591} = 2.5783 \times 10^{-6} \) F

b)
Le facteur de qualité est donné par
\( Q = \dfrac{\omega_{r}}{\omega_{c_2} - \omega_{c_1}} = \dfrac{100 \sqrt{247} \pi}{1900 \pi - 1300 \pi } = 2.62\)

Plus de Références et Liens

• Calculateur de Circuit RLC Série Résonant
• Circuits série RLC
• Calculateur d'Impédance de Circuit RLC Série
• Calculateur d'Impédance de Circuit RLC Parallèle
• Calculateur de Graphique de Courant RLC Série